
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контроль по альтернативному признаку
Предположим, что контролируется партия из N изделий. Для контроля делается случайная выборка объемом п. Количество способов, которыми можно выбрать пизделий из N без учета порядка следования - это число сочетаний

Пусть случайная величина X—количество дефектных (несоответствующих) изделий в выборке. Известно, что во всей партии изделий доля несоответствий составляет q. Тогда число дефектных изделий в партии равно Nq, число годных изделий составитN — Nq. Рассмотрим событие X = т — взято ровно т дефектных изделий. Это возможно, если из Nqдефектных изделий взято т изделий, а из оставшихся годных N — Nqвзято п — т изделий (всего в выборке п изделий). Тогда вероятность рассматриваемого события
 (5.1)
(5.1)
Формула (5.1) описывает гипергеометрическое распределение.
Как правило, объем выборки составляет не более 10% от объема всей партии, в этом случае гипергеометрическое распределение может быть аппроксимировано биномиальным
P(X = m) =Cmnqm(1-q)n-m. (5.2)
На практике доля несоответствий обычно составляет менее 10%, в этом случае в свою очередь биномиальное распределение может быть аппроксимировано распределением Пуассона:
 (5.3)
(5.3)
Рассмотрим одноступенчатый контроль по альтернативному признаку. Вероятность приемки партии P(q) в этом случае — это вероятность того, что количество дефектных изделий т в выборке не превысит приемочное число с. Используя формулу сложения вероятностей несовместных событий, получим уравнение оперативной характеристики одноступенчатого плана контроля:
P(q) = Р(т <с) – Р(Х = 0) + Р(Х = 1)+...+Р(Х = с) =  (X=m).
(X=m).
В частности, при использовании биномиального распределения (5.2) уравнение оперативной характеристики одноступенчатого плана примет вид:
Используя это уравнение, из рис. 5.3 получим следующие соотношения:
p(aql) =  (5.6)
(5.6)
p(lq)= 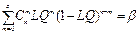 .
.
Решая численно систему нелинейных уравнений (5.6) при известных значениях AQLи LQ, а также заданных рисках а и (3, находят параметры плана - объем выборки пи приемочное число с.
Анализ зависимостей (5.4) - (5.5) показывает, что при постоянном объеме выборки пс возрастанием приемочного числа с вероятность принятия партии с заданным приемлемым уровнем качества AQLвозрастает (рис. 5.4, а),а с возрастанием ппри постоянном с вероятность приемки партии уменьшается (рис. 5.4, б). Можно подобрать такой план контроля (п,с), который бы обеспечивал значения рисков аир при заданных значениях уровней качества AQLи LQ.
 Рис. 5.4. Оперативные характеристики при п - const (о) и с = const(6)
Рис. 5.4. Оперативные характеристики при п - const (о) и с = const(6)
По результатам контроля множества партий продукции могут быть найдены некоторые полезные характеристики, в частности, средняя доля несоответствующих единиц продукции в принятых партиях (средний уровень выходного качества) и среднее число проконтролированных изделий в партии.
Рассмотрим одноступенчатый план, при котором забракованные партии изделий подвергаются сплошному контролю, т.е. контролируются все оставшиеся (N-п)изделия партии, а выявленные дефектные изделия заменяют годными. Предположим, что доля дефектных изделий постоянна и равна д. Тогда с вероятностью P(q) партии изделий принимаются (доля дефектных изделий в ней приблизительно равна а),а с вероятностью (1 -P(q)) партии подвергаются сплошному контролю; доля дефектных изделий в этих партиях равна нулю. Тогда средняя доля дефектных изделий в принятых партиях по формуле математического ожидания для дискретной случайной величины равна:
qcp=qP(q)+0[l-P(q)]=qP(q). (5.7)
Величина qcpи называется средним уровнем выходного качества. Из формулы (5.7) видно, что при q= 0 значение qc= 0 и при q= 1 также qcp = 0, поскольку вероятность Р(1) = 0. Так как qcp — неотрицательная функция от q, равная нулю при q = 0 и q= 1, то внутри интервала 0 <q<1 средний выходной уровень дефектности имеет максимум qmax(рис. 5.5). Максимальный для заданного плана контроля средний уровень qmaxназывают пределом среднего уровня выходного качества.
При использовании рассмотренного выше плана, когда забракованные партии изделий подвергаются сплошному контролю, число проконтролированных в партии объема N изделий есть случайная величина, принимающая значение пс вероятностью Р(д) изначение N (сплошной контроль) с вероятностью (1 — P(q)). Поэтому среднее число проконтролированных изделий в партии равно: ncp = nP(q)+N(1-P(q)). (5.8)
 Рис. 5.5. Предел среднего уровня выходного качества.
Рис. 5.5. Предел среднего уровня выходного качества.
Если же принято решение о возврате забракованной партии поставщику, то объем контроля в этом случае постоянен и равен объему выборки п.
Для уменьшения объема контроля используют многоступенчатые и в частности двухступенчатые планы. При использовании двухступенчатого плана решение о качестве партии принимается либо после анализа первой выборки объемом пх,с приемочным числом с,, и браковочным dx,либо второй объемом «2 с приемочным числом с2.
Найдем уравнение оперативной характеристики двухступенчатого плана. Учитывая, что приемка производится или на первой ступени контроля, или на второй, получим: P1(q)= P1 (q) + P2(q), что представляет собой сумму вероятностей несовместных событий. Вероятность приемки партии на первой ступени по аналогии с (5.4) определяется по формуле
P1(q) = ∑ P(Х1= т1), где Р(Х1=т1)- вероятность того, что в первой выборке окажется ровно т1дефектных изделий).
Вероятность приемки партии на второй ступени - это вероятность одновременного осуществления двух независимых событий: количество дефектных изделий т1в первой выборке удовлетворяет условию с1<т1<dx,при этом количество дефектных изделий в двух выборках не превышает приемочное число на второй ступени контроля (т1 + т2) < с2:

Тогда уравнение оперативной характеристики двухступенчатого примет вид:
 .
.
Вероятности, входящие в это уравнение, определяются в зависимости от используемого распределения — гипергеометрического, биномиального или Пуассона - соответственно по формулам (5.1), (5.2) или (5.3).
Для оценки среднего числа проконтролированных изделий рассмотрим, как и при одноступенчатом контроле, два возможных варианта. В случае если отклоненные партии бракуются (возвращаются поставщику), среднее число проверенных изделий в партии определяется по формуле

Здесь, как и ранее, использована формула математического ожидания дискретной случайной величины: для отклонения партии первая выборка берется в любом случае (вероятность этого события - единица), а вторая - при условии, что с1<т1<d1.
В другом варианте, если отклоненные партии изделий подвергаются сплошному контролю, то партия объемом N может быть принята либо по результатам первой выборки, и тогда в ней будет проконтролировано п1изделий, либо на основании двух выборок и в ней будет проконтролировано (п1 + п2) изделий. Если же партия отклоняется, то проверяются все N изделий.
Дата добавления: 2015-04-18; просмотров: 84; Мы поможем в написании вашей работы!; Нарушение авторских прав |