Основные свойства преобразования Фурье.

1. Сдвиг сигнала во времени Пусть сигнал s₁(t) произвольной формы существует на интервале времени от t₁ до t₂ и обладает спектральной плотностью S₁(Ω). При задержке этого сигнала на величину t₀ (при сохранении его формы) получим новую функцию времени s₂(t)=s₁(t-t₀),

существующую на интервале от t₁ + t₀ до t₂ + t₀.

Спектральная плотность сигнала s₂(t) в соответствии

Вводя новую переменную интегрирования τ = t — t₀, получаем

2. Изменение масштаба времени Пусть сигнал s₁{t), изображенный на рис.1 сплошной линией, подвергся сжатию во времени. Новый, сжатый сигнал s₂(t) (пунктир­ная кривая на рис. 1) связан с исходным сигналом s₁(t) соотношением s₂(t)=s₁(nt).

Длительность импульса s₂(t) в п раз меньше, чем у исходного им­пульса, и равна T/n(n>1).

Спектральная плотность сжатого импульса

Вводя новую переменную интегрирования τ = nt, получаем

Но интеграл в правой части этого выражения есть не что иное, как спектральная плотность исходного сигнала s₁(t) при частоте Ω /n, т. е. S₁(Ω/n).

Таким образом,

Итак, при сжатии сигнала в п раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плот­ности при этом уменьшается в п раз.

Очевидно, что при растягивании сигнала во времени (т. е. при п < 1) имеет место сужение спектра и увеличение модуля спектраль­ной плотности.

3. Дифференцирование и интегрирование сигнала Дифференцирование сигнала s(t) можно рассматривать как почлен­ное дифференцирование всех гармонических составляющих, входящих в его спектр.

Общий вид гармонической составляющей сигнала s(t) при частоте Ω можно представить в форме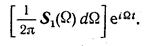

Заключенную в квадратные скобки величину можно рассматривать как амплитуду колебания в полосе dΩ.

Дифференцирование по времени t дает

Следовательно, спектральная плотность производной ds(t)/dt равна

Аналогично, спектральная плотность интеграла ∫s(t)dt равна

4. Сложение сигналов Так как преобразование Фурье, определяющее спектральную плотность заданной функции времени, является линейным преобразованием, то очевидно, что при сложении сигналов s₁(t), s₂(t) и т. д., обла­дающих спектрами Si(Ω), S_t(Ω) и т. д., суммарному сигналу s(t)=s₁(t)+s₂(t)+… соответствует спектр S(Ω) = S₁(Ω) + S₂(Ω)+…

5. Произведение двух функций Пусть рассматриваемый сигнал s(f) является произведением двух функций времени f(t) и g(t).

Применив общую формулу, определим спектр сигнала s(t):

Каждую из функций f(t) и g(t) можно представить в виде интеграла Фурье:

Подставляя в предыдущее выражение второй из этих интегралов, получаем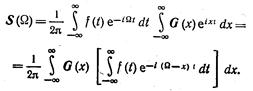

Заключенный в квадратные скобки интеграл представляет собой спектральную плотность функции f(f) при частоте Ω — х, т. е. F(Ω — х).

Следовательно, Итак, спектр произведения двух функций времени f(t) и g{t) равен (с коэффициентом 1/2π) свертке их спектров F( Ω) и G(Ω).

6. Энергетический спектр сигнала. Корреляционная функция детерми­нированного сигнала.

Основными энергетическими характеристиками вещественного сигнала s (t)

являются его мощность и энергия.

Мгновенная мощность определяется как квадрат мгновенного значения s(t):

Если s (t) — напряжение или ток, то р(t) есть мгновенная мощность выделяемая на сопротивлении в 1 Ом. Энергия сигнала на интервале t₂, t₁ определяется как интеграл от мгновенной мощности: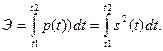

Отношение

имеет смысл средней на интервале t₂, t₁ мощности сигнала.

Реальные сигналы имеют конечную длительность и ограниченную по величине мгновенную мощность. Энергия таких сигналов конечна.

Пусть сигнал s (t) (ток, напряжение) представляет собой сложную периодическую функцию времени с периодом Т. Энергия такого сигнала, длящегося от t =-∞ до t = ∞, бесконечно велика. Основной интерес представляют средняя мощность периодического сигнала и распределение этой мощности между отдельными гармониками. Очевидно, что средняя мощность сигнала, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период Т. Поэтому можно

воспользоваться формулой (1.1)

в которой под коэффициентами с_n следует подразумевать коэффициенты ряда

(1.2)

под интервалом ортогональности t₂ – t₁— величину периода T, а под нормой - величину

Таким образом, средняя мощность периодического сигнала

(1.3)

Используя тригонометрическую форму ряда Фурье и учитывая, что c₀=a₀/2 и получаем (1.4)

Если s {t) представляет собой ток i(t), то при прохождении его через сопротивление г выделяется мощность (средняя) (1.5)

где I₀= а₀/2 — постоянная составляющая, а I_mn = А_n — амплитуда n-й гармоники тока i(t).

Итак, полная средняя мощность равна сумме средних мощностей, выделяемых отдельно постоянной составляющей I₀ и гармониками с амплитудами I_mn. Это означает, что средняя мощность не зависит от фаз отдельных гармоник. Это вытекает из ортогональности спектральных составляющих, в данном случае на интервале Т.

Для непериодического колебания конечной длительности усреднение энергии за бесконечно большой период дает нуль и, следовательно, средняя мощность такого колебания равна нулю. В этом случае связь между энергией сигнала и модулем его спектральной плотности определяется равенства Парсеваля (1.6)

где - спектр сигнала s(t), - модуль этого спектра.

Между выражениями (1.4) и (1.6) имеется существенное различие.

Выражение (1.4) определяет среднюю мощность периодического колебания. Операция

усреднения осуществлялась делением энергии отрезка колебания за один период на величину Т.

Для непериодического колебания конечной длительности усреднение энергии за бесконечно большой период дает нуль и, следовательно, средняя мощность такого колебания равна нулю. Важно отметить, что энергия непериодического сигнала не зависит от фазировки спектральных составляющих. Это является, как и для периодического сигнала, результатом ортогональности спектральных составляющих. Различие заключается лишь в интервалах ортогональности: период Т для периодического сигнала и бесконечно большой интервал для непериодического сигнала.

Из выражения (1.6) видно, что величину , имеющую смысл энергии, приходящейся на 1 Гц, можно рассматривать как спектральную плотность энергии сигнала.

Наряду со спектральным подходом к описанию сигналов часто на практике оказывается необходимой характеристика, которая да­вала бы представление о некоторых свойствах сигнала, в частности о скорости изменения во времени, без разложения его на гармони­ческие составляющие.

В качестве такой «временной» характеристики широко использует­ся автокорреляционная функция сигнала.

Для детерминированного сигналаs(t)конечной длительности авто­корреляционная функция определяется следующим выражением: (1.7.)

где τ – величина временного сдвига сигнала.

Из выражения (1.7) видно, что характеризует степень свя­зи (корреляции) сигнала s(t) с его копией, сдвинутой на величину τ по оси времени.

Ясно, что функция достигает максимума при τ = 0, так как любой сигнал полностью коррелирован с самим собой. При этом (1.8)

т.е. максимальное значение автокорреляционной функции равно энергии сигнала.

С увеличением τ функция убывает (не обязательно монотонно) и при относительном сдвиге сигналов s(t) и s(t-τ)на величину, превышающую длительность сигнала, обращается в нуль. На рис.1.1. показано построение автокорреляционной функции для простейшего сигнала в виде прямоугольного импульса (рис.1.1а). Сдвинутый на τ (в сторону запаздывания) сигнал) s(t-τ)показан на рис.1.1б, а произведение — на рис.1.1в. График функции изображен на рис.1.1 а. Каждому значению τ соот­ветствует свое произведение и своя площадь под графиком функции .Численные значения таких площадей для соот­ветствующих τи дают ординаты функции