Случайные сигналы. Стационарные случайные процессы. Свойство эргодичности.

Информация, передаваемая по каналу связи или извлекаемая в результате измерения, заключена в сигнале.

До приема сообщения (до испытания) сигнал следует рассматривать как случайный процесс, представляющий собой совокупность (ансамбль) функций времени, подчиняющихся некоторой общей для них статистической законо­мерности. Одна из этих функций, ставшая полностью известной после прие­ма сообщения, называется реализацией случайного процесса. Эта реализация является уже не случайной, а детерминированной функцией времени.

Важной, но не исчерпывающей характеристикой случайного процесса является присущий ему одномерный закон распределения вероятностей.

На рис.1.19 изображена совокупность функций х₁(t), х₂(t), ..., образую­щих случайный процесс X(t). Значения, которые могут принимать отдель­ные функции в момент времени t =t₁ образуют совокупность случайных ве­личин х₁(t), х₂(t), ...

Вероятность того, что величи­на x_k(t₁)при измерении попадает в какой-либо заданный интервал (а, b) (рис.1.19), определяется вы­ражением

P_t1 (а < х b) (1.132)

Рис.1.19. Совокупность функций, образующих случайный процесс

Функция р(х; t₁) представляет собой дифференциальный закон распределения случайной величины х(t₁); р(х; t₁) называется одномер­ной плотностью вероятности, аP_ti - интегральной вероятностью.

Функция р(х; t_t) имеет смысл для случайных х непрерывного типа, могущих принимать любое значение в некотором интервале. При любом характере функции р(х; t₁) должно выполняться равенство

(1.133)

где x_min и x_mах — границы возможных значений х(t₁).

Если же х является случайной величиной дискретного типа и может принимать любое из конечного числа дискретных значений, то (1.133) следует заменить суммой

где P_i — вероятность, соответствующая величине x_i.

Задание одномерной плотности вероятности р(х;t₁) позволяет произве­сти статистическое усреднение как самой величины х, так и любой функции f(х). Под статистическим усреднением подразумевается усреднение х по множеству (по ансамблю) в каком-либо «сечении» процесса, т. е. в фиксиро­ванный момент времени.

Для практических приложений наибольшее значение имеют следующие параметры случайного процесса:

математическое ожидание (

дисперсия

Средне-квадратическое отклонение

Одномерная плотность вероятности недостаточна для полного описа­ния процесса, так как она дает вероятностное представление о случайном процессе X(t) только в отдельные фиксированные моменты времени. Более полной характеристикой является двумерная плотность вероятности^[1] р(х₁ ,х₂; t₁ ,t₂), позволяющая учитывать связь значений х₁ и х₂, принимае­мых случайной функцией в произвольно выбранные моменты времени t₁ и t₂.

Исчерпывающей вероятностной характеристикой случайного процесса является п-мерная плотность вероятности при достаточно больших п. Од­нако большое число задач, связанных с описанием случайных сигналов, уда­ется решать на основе двумерной плотности вероятности.

Задание двумерной плотности вероятности р (х₁ ,х₂;t₁, t₂) позволяет, в частности, определить важную характеристику случайного процесса — ковариационную функцию 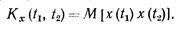(1.236)

Согласно этому определению ковариационная функция случайного процесса X (t) представляет собой статистически усредненное произведение значений случайной функции X (t) в моменты t₁ и t₂.

Для каждой реализации случайного процесса произведение х(t₁) х(t₂) является некоторым числом. Совокупность реализаций образует множество случайных чисел, распределение которых характеризуется двумерной плот­ностью вероятности р(х₁ ,х₂; t₁ ,t₂). При заданной функции р(х₁ ,х₂; t₁, t₂) операция усреднения по множеству осуществляется по формуле

(1.137)

При t₂ = t₁ двумерная случайная величина х₁х₂ вырождается в одно­мерную величину х₁²₌ х₂² . Можно поэтому написать

(1.138)

Таким образом, при нулевом интервале между моментами времени t₁ и t₂ ковариационная функция определяет величину среднего квадрата слу­чайного процесса в момент t = t₁.

При анализе случайных процессов часто основной интерес представляет его флуктуационная составляющая. В таких случаях применяется корре­ляционная функция.

(1.139)

Подставляя в (1.138) — т_х вместо и — т_х (t₂) вме­сто х (t₂), можно получить следующее выражение:

(1.140)

При t₁ = t₂ = t выражение (1.139) в соответствии с (1.135) определяет дисперсию случайного процесса D_x(t). Следовательно,

Исследование случайного процесса, а также воздействия его на радио­цепи существенно упрощается при стационарности процесса.

Случайный процесс называется строго стационарным, если его плотность вероятности р (х₁ ,х₂, ..., х_п; t₁ ,t₂, ..., t_n) произвольного порядка п зависит только от интервалов t₂—t₁, t₃—t₁, ..., t_n—t₁ и не зависит от положения этих интервалов в области изменения аргумента t.

В радиотехнических приложениях теории случайных процессов условие стационарности обычно ограничивается требованием независимости от вре­мени только одномерной и двумерной плотностей вероятности (случайный процесс, стационарный в широком смысле). Выполнение этого условия поз­воляет считать, что математическое ожидание, средний квадрат и дисперсия случайного процесса не зависят от времени, а корреляционная функция за­висит не от самих моментов времени t₁ и t₂ , а только от интервала между ними τ = t₂ — t₁.

Стационарность процесса в широком смысле можно трактовать как ста­ционарность в рамках корреляционной теории (для моментов не выше вто­рого порядка).

Таким образом, для случайного процесса, стационарного в широком смысле, предыдущие выражения можно записывать без обозначения фикси­рованных моментов времени. В частности,

(1.141)

(1.142)

(1.143)

(1.144)

(1.145)

Дальнейшее упрощение анализа случайных процессов достигается при использовании условия эргодичности процесса. Стационарный случайный процесс называется эргодическим, если при определении любых

статистиче­ских характеристик усреднение по множеству реализаций эквивалентно ус­реднению по времени одной теоретически бесконечно длинной реализации.

Условие эргодичности случайного процесса включает в себя и условие его стационарности. В соответствии с определением эргодического процесса соотношения (1.142)—(1.145) эквивалентны следующим выражениям, в кото­рых операция усреднения по времени обозначена чертой:

(1.146)

(1.147)

(1.148)

(1.149)

(1.150)

Если х(t) представляет собой электрический сигнал (ток, напряжение), то постоянная составляющая случайного сигнала, R_x(0) = — средняя мощность флуктуации сигнала [относительно постоянной состав­ляющей х(t)].

Выражение (1.147) внешне совпадает с определением корреляци­онной функции детерминированного сигнала (периодического).

Часто применяется нормированная корреляционная функция

(1.151)

Функции К_х(τ), R_x(τ) и r_х(τ) характеризуют связь (корреляцию) между значениями х(t), разделенными промежутком τ. Чем медленнее, плав­нее изменяется во времени х(t), тем больше промежуток τ, в пределах ко­торого наблюдается статистическая связь между мгновенными значениями случайной функции.