Уравнение колебательного движения МТ. Колебания при гармоническом возмущении в среде с линейным сопротивлением.

Рассмотрим движение МТ под действием центральной силы, стремящейся возвратить МТ в равновесное положение при ее отклонении от этого положения. Если начальное отклонение МТ и ее начальная скорость совпадают по направлению, то МТ под действием такой силы будет совершать прямолинейное движение. Будем считать, что сила, стремящаяся возвратить МТ в равновесное положение, пропорциональна ее отклонению от центра (рис.1):

,

где с – коэффициент пропорциональности. Такую силу в дальнейшем будем называть восстанавливающей.

Пусть кроме восстанавливающей силы приложена сила сопротивления, пропорциональная скорости ее движения

,

где – коэффициент, характеризующий интенсивность сопротивления движению МТ.

Пусть к точке приложена еще и возмущающая сила, изменяющаяся с течением времени по гармоническому закону и направленная по оси х (рис. 1):

H_в = H sin pt,

где Н и р - соответственно амплитуда (наибольшее значение) и круговая частота возмущающей силы.

Рис. 1

Дифференциальное уравнение движения в проекции на ось Х примет вид:

.

Приводя это уравнение к каноническому виду, получим:

, (1)

где .

Это линейное, линейное неоднородное дифференциальное уравнение второго порядка. Решение этого уравнения состоит из двух частей:

х = х₁+х₂, (2)

где х₁ – общее решение однородного уравнения

, (3)

х₂ – частное решение неоднородного уравнения

. (4)

Для решения однородного уравнения составим характеристическое уравнение:

,

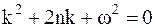где k – характеристическое число.

Решения характеристического уравнения имеют вид:

.

Возможны три типа корней характеристического уравнения:

n<w (случай малого сопротивления),

тогда 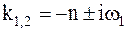– комплексные числа ( 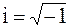, ), решение однородного уравнения (3) имеет вид:

, (5)

где а и a – постоянные интегрирования.

n>w (случай большого сопротивления),

тогда – действительные отрицательные числа, решение однородного уравнения (1.16) имеет вид:

,

где С₁ и С₂ – постоянные интегрирования.

n=w,

тогда – кратные действительные отрицательные числа, решение однородного уравнения (1.16) имеет вид:

,

где С₁ и С₂ – постоянные интегрирования.

Частное решение ищем с учетом вида правой части:

, (6)

где b и b – постоянные интегрирования, которые нужно подобрать так, чтобы неоднородное уравнение (1) обратилось в тождество.

Подставляя значения х₂, в неоднородное уравнение, получим:

Отсюда, с учетом формул для синуса и косинуса суммы двух углов, имеем:

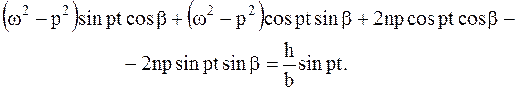
Приравнивая коэффициенты при sin pt и cos pt в правой и левой частях этого уравнения, получим систему двух уравнений относительно sin b и cos b:

Решая систему, найдем:

,

.

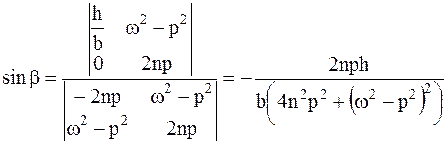Возведя в квадрат первое и второе выражения и сложив их, получим:

, (7)

а поделив первое на второе:

или

. (8)

Общее решение, например, в случае малого сопротивления среды может быть представлено в виде:

, (9)

где а и a - постоянные интегрирования, определяемые начальными условиями движения, а значения b и b только что были определены и от начальных условий не зависят. Для определения постоянных интегрирования (а, a) полное решение (9) необходимо удовлетворить начальным условиям.

Таким образом, колебания МТ являются результатом наложения (суперпозиции) собственных (первое слагаемое в правой части соотношения (9)) и вынужденных (второе слагаемое в правой части соотношения (9)) колебаний.

Наличие множителя e^-nt обусловливает быстрое затухание собственных колебаний. Поэтому при расчетах в основном приходится считаться с вынужденными колебаниями, которые являются гармоническими с амплитудой b, угловой частотой p, равной частоте возмущающей силы, и начальной фазой b.

Исследуем зависимость амплитуды вынужденных колебаний и начальной фазы от частоты возмущающей силы и сопротивления среды. Разделив в формулах для амплитуды b (7) и фазы b (8) вынужденных колебаний числитель и знаменатель на w², перепишем их в следующем виде:

,

,

где – величина статического отклонения МТ под действием силы Н, равной максимальному значению вынуждающей силы H_в;

– отношение круговых вынужденных и собственных частот колебаний МТ (коэффициент расстройки);

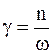– величина, характеризующая сопротивление среды (коэффициент затухания).

Исследуем то, как будет изменяться амплитуда вынужденных колебаний в зависимости от изменения безразмерных параметров z и γ. Для этого рассмотрим подкоренное выражение в знаменателе амплитуды:

.

При f(z, γ) = 1 и b = δ независимо от значения γ.

Для исследования функции f(z, γ) найдем производную по параметру z:

.

Пусть сопротивление движению невелико и 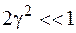. Тогда при возрастании z от 0 для малых z будет , следовательно, знаменатель амплитуды вынужденных колебаний убывает, а амплитуда b растет. Приравнивая производную нулю, находим значения параметра z, при которых функция f(z, γ) имеет экстремум:

,

так как параметр z не может быть меньше нуля, то исключается значение .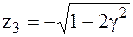

Результаты исследования на максимум амплитуды вынужденных колебаний b в зависимости от z при различных значениях g отражены на рис. 2.(график зависимости амплитуды от частоты, амплитудно-частотная характеристика системы (АЧХ), если по оси ординат отложить b/ - график динамического коэффициента (коэффициента динамичности))

Рис. 2