Вопрос 25

Магнитный поток (поток магнитной индукции)через поверхность определенной площади — физическая величина, равная скалярному произведению вектора магнитной индукции на вектор площади: 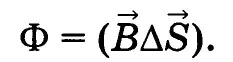Единица магнитного потока — вебер (1 Вб) 1 Вб= 1 Тл•м².

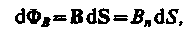где Вn = Всоs. — проекция вектора В на направление нормали к площадке dS ( — угол между векторами n и В), dS = dSn— вектор, модуль которого равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора магнитной индукции F_B через произвольную поверхность S равен 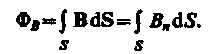Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, B_n = B = constи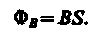

Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

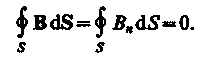Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.