Кольцо вычетов

Рассмотрим множество всех классов вычетов по модулю . Класс состоит из всех чисел вида , где tпробегает множество Z, т. е.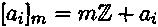

Следовательно, классы вычетов по модулю та совпадают со смеж­ными классами кольца Z по его идеалу mZ.

Теорема 1. Определение операций сложения и умножения классов вычетов по формулам

корректно, и множество с этими операциями является коммутативным кольцом с единицей. Это есть факторкольцо кольца Zпо его идеалу тZ.

Кольцо Z/rn называют кольцом классов вычетов по модулю т.

Опишем обратимые элементы этого кольца.

Теорема 2.Элемент обратим в кольце Z/mтогда и только тогда, когда класс взаимно прост с т, т. е. (а,т) = 1.

Китайская теорема об остатках

Пусть m - натуральное число, m₁, m₂, ..., m_t - взаимно простые натуральные числа, произведение которых больше либо равно m.

Теорема:

Любое число x: 0 <= x <= m может быть однозначно представлено в виде последовательности r(x) = (r1, r2, ..., rt), где ri = x(mod mi).

Для любых чисел r1 .. rt, таким образом, существует единственное число x(mod m), такое что

x = ri(mod mi), 1 <= i <= t

Более того, любое решение x набора такого сравнений имеет вид

x = r1*e1 + ... + rt*et (mod m), где ei = m / mi * ( ( m/mi )-1 mod mi ), 1 <= i <= t.

Системы линейного уравнения над кольцом и полем. Системы линейных уравнений над коммутативным кольцом с единицей. Равносильность систем. Системы уравнений над кольцом. Однородные уравнения и функциональная система решений.

Алгоритмы на графах. Обход графа в глубину, построение глубинного остового леса и классификация ребер, не вошедших в лес. Алгоритмы нахождения связных компонентов неориентированных графов и сильно связных компонентов ориентированных графов. Поиск в ширину и кратчайшие пути в графе.

Обход в глубину— это обход связного графа (или компоненты связности) по следующим правилам (алгоритм обхода):

1)Рассматриваем вершину Х.Двигаемся в любую другую, ранее непосещенную вершину (если таковая найдется), одновременно запоминая дугу, по которой мы впервые попали в данную вершину;

2) Если из вершины Хнельзя попасть в ранее непосещенную вершину или таковой нет, то возвращаемся в вершину Z, из которой впервые попали в X, и продолжаем обход в глубину из вершины Z.

3) Такой обход графа продолжается до тех пор, пока очередная вершина Х, не совпадет с вершиной Х₀,с которой начался обход графа (компоненты связности).

Обход в ширину — это обход связного графа (или компоненты связности) по следующим правилам (алгоритм обхода):

1)Рассматриваем вершину Х. Ей присваивается метка 0;

2) Всем смежным вершинам с вершиной с меткой 0 поочередно присваиваются метки 1;

3) Всем смежным вершинам с вершинами с меткой 1 поочередно присваиваются метки 2;

4) И т.д. до тех пор, пока не будут помечены все вершины в текущем графе (компоненте связности).