
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение систем логических уравнений
Решить систему логических уравнений значит найти такие наборы значений переменных, входящих в уравнения, при которых ВСЕ уравнения системы превращаются в верные равенства. Для решения таких задач существует несколько методов. Выбор метода определяется особенностями задачи. Самый простой метод – табличный, однако когда в системе имеется до десятка переменных, составление таблицы может оказаться слишком трудоемким.
Пример. Сколько различных решений имеет логическое уравнение
(X1 Ú X2) Ù (X2 Ú X3) Ù (X3 Ú X4) Ù (X4 Ú X5) Ù (X5 Ú X6) = 1
где x1, x2, …, x6 – логические переменные?
Решение. Уравнение можно переписать в более простой форме, учитывая, что x®y= 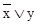 :
:
(x1®x2)(x2®x3)(x3®x4)(x4®x5)(x5®x6)=1
При 6 переменных число их комбинаций равно 64. Можно начать составлять таблицу истинности для данного логического выражения, чтобы определить, какие варианты значений переменных х1-х6 можно отбросить как неподходящие:
| X1 | Х2 | Х3 | Х4 | Х5 | Х6 | F |
Уже на основе этих наборов можно предположить, что наборы, в которых рядом будут стоять 1 и 0, не являются решениями (1®0=0). Таких наборов большинство, исключениями являются только 000000, 000001, 000011 (см. таблицу), а также 000111, 001111, 011111, 111111 – всего 7 решений.
Табличный метод решения можно применять поэтапно. Для этого сначала определяются решения для первого уравнения системы с учетом входящих в него переменных, затем решается системы из первого и второго уравнения с подключением переменных второго уравнения, но в пределах допустимых значений, являющихся также решением первого уравнения, затем подключается третье уравнение и т.д.
Пример. Сколько различных решений имеет система уравнений
(X1 Ù X2) Ú (X1 Ù X2) Ú (X1 º X3) = 1
(X2 Ù X3) Ú (X2 Ù X3) Ú (X2 º X4) = 1
...
(X8 Ù X9) Ú (X8 Ù X9) Ú (X8 º X10) = 1
Решение. Система с 10 переменными предполагает 1024 возможных набора значений переменных. Для начала систему можно переписать в более удобном виде:
(X1 º X2) Ú (X1 º X3) = 1
(X2 º X3) Ú (X2 º X4) = 1
...
(X8 º X9) Ú (X8 º X10) = 1
Для начала нужно найти решения первого уравнения:
| Х1 | Х2 | Х3 | F |
| | | | |
| | | | |
Первое уравнение имеет 6 решений. Каждое из этих решений при подключении второго уравнения и переменной Х4 станет основой для двух возможных наборов переменных Х1-Х4 (например, 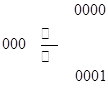 ):
):
| Х1 | Х2 | Х3 | Х4 | F |
| | | | | |
| | | | | |
Система из двух уравнений имеет 10 решений. Подключим третье уравнение и переменную Х5:
| Х1 | Х2 | Х3 | Х4 | Х5 | F |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
Система из 3 уравнений имеет 16 решений. Закономерность нарастания числа решений уже становится очевидной: 16=10+6, т.е. число решений на следующем шаге – сумма двух предыдущих. Тогда:
Для 3 переменных – 6 решений
Для 4 переменных – 10 решений
Для 5 переменных – 16 решений
Для 6 переменных – 26 решений
Для 7 переменных – 42 решения
Для 8 переменных – 68 решений
Для 9 переменных – 110 решений
Для 3 переменных – 178 решений
Для некоторых сложных уравнений можно воспользоваться подстановками, т.е. ввести новые логические переменные, которые представляют собой комбинации исходных переменных. Однако для этого переменные, входящие в подстановочные, должны быть независимыми (т.е. наборы переменных в разных подстановках не должны повторяться).
Пример. Сколько различных решений имеет система уравнений
((X1 º X2) Ù (X3 º X4)) Ú ((X1 º X2) Ù (X3 º X4)) = 1
((X3 º X4) Ù (X5 º X6)) Ú ((X3 º X4) Ù (X5 º X6)) = 1
((X5 º X6) Ù (X7 º X8)) Ú ((X5 º X6) Ù (X7 º X8)) = 1
((X7 º X8) Ù (X9 º X10)) Ú ((X7 º X8) Ù (X9 º X10)) = 1
Решение. Для упрощения системы можно ввести следующие подстановки:
Y1=X1 º X2; Y2=X3 º X4; Y3=X5 º X6; Y4=X7 º X8; Y5=X9 º X10
Тогда система уравнений будет выглядеть так:
Y1×Y2 Ú Y1×Y2 = 1 Y1ºY2=1
Y2×Y3 Ú Y2×Y3 = 1 или Y2ºY3=1
Y3×Y4 Ú Y3×Y4 = 1 Y3ºY4=1
Y4×Y5 Ú Y4×Y5 = 1 Y4ºY5=1
Получилась система с 5 переменными. Сколько у нее решений?
| Y1 | Y2 | Y3 | Y4 | Y5 | F |
| … | |||||
Очевидно, решений только 2 – все 0 или все 1.
Теперь нужно рассмотреть, какие значения переменных Х1-Х10 соответствуют этим решениям:
1) При Y1= X1 º X2=0: X1¹X2, т.е. Х1=0, Х2=1 или Х1=1, Х2=0
2) При Y2= X3 º X4=0: X3¹X4, т.е. Х3=0, Х4=1 или Х3=1, Х4=0
3) При Y3= X5 º X6=0: X5¹X6, т.е. Х5=0, Х6=1 или Х5=1, Х6=0 и т.д.
Получается, что для каждого значения Y существует по две возможных комбинации Х, т.е. общее число решений для Y1=Y2=Y3=Y4=Y5=0 равно 25=32. Столько же решений можно найти и для Y1=Y2=Y3=Y4=Y5=1. Всего решений будет 32+32=64.
Пример. Сколько различных решений имеет система уравнений (знак «!» означает отрицание, «&» - логическое И, «+» - ИЛИ).
(!(A=B)&(C=D))+((A=B)&!(C=D))=1
(!(A=C)&(D=E))+((A=C)&!(D=E))=1
(!(A=D)&(E=F))+((A=D)&!(E=F))=1
(!(A=E)&(F=G))+((A=E)&!(F=G))=1
A=1
E=1
Решение.
Сначала можно упростить выражения:
(A=B)Å(C=D)=1
(A=C)Å(D=E)=1
(A=D)Å(E=F)=1
(A=E)Å(F=G)=1
A=1
E=1
Далее можно решать табличным методом. Найдем решения первого уравнения (в таблице будет только 8 строк, т.к. А=1):
| A | B | C | D | x |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Теперь введем в таблицу переменную Е=1:
| A | B | C | D | Е | x |
| | | | | | |
| | | | | | |
Затем будем последовательно добавлять переменные F и G:
| A | B | C | D | Е | F | x |
| | | | | | | |
| | | | | | | |
| A | B | C | D | Е | F | G | x |
| | | | | | | | |
| | | | | | | | |
Система имеет два решения.
Пример.Сколько решений имеет система логических уравнений?
х1®х2®х3®х4®х5®х6=1
у1®у2®у3®у4®у5®у6=1
х1®у1=1
Решение. Можно решить задачу через таблицу истинности (212 варианта), но лучше найти закономерность нарастания числа решений.
Начать можно с четырех переменных. Для системы
х1®х2 =1
у1®у2 =1
х1®у1=1
число решений первого уравнения можно найти из таблицы истинности:
| х1 | х2 | х1®х2 |
Система имеет 3 решения (два из них получаются при первом аргументе равном 0, одно – при первом аргументе, равном 1, т.е. каждый ноль дает одно решение, а единицы – по одному решению на две единицы).
По аналогии второе уравнение (у1®у2 =1) будет иметь такое же число решений. Совместное решение первого и второго уравнений имело бы 9 решений (по три решения для у на каждое решение для х), но третье уравнение (х1®у1 =1) накладывает свои ограничения: нам нужны только такие комбинации, где не будет сочетаний х1=1, у1=0:
| х1 | х2 | у1 | у2 | х1®у1 |
Система имеет 7 решений, которые можно получить из следующего рассуждения: каждый аргумент х1, равный 0, дает 3 решения, т.е. число решений первого или второго уравнения (х1®х2 =1 или у1®у2 =1). Если же аргумент х1 равен 1, то для решения системы подходит только один вариант, при котором у1¹0.
В таком виде из числа возможных решений первого или второго уравнения два получены при х1=0 и одно при х1=1.
Число решений 2*3+1=7.
Добавим в систему х3 и у3. Число решений первого уравнения:
| х1 | х2 | х3 | х1®х2®х3 |
Система имеет 5 решений (там, где х1®х2=1 получаем по одному решению, для х1®х2=0 – по два; иди другое вычисление: при решении уравнения х1®х2=1 получено 3 единичных решения и 1 нулевое; каждое единичное решение дало по одному варианту для решения х1®х2®х3=1, каждое нулевое – по два, т.е. 3*1+1*2=5 решений).
В найденных решениях в двух случаях х1=0, в трех случаях х1=1.
По аналогии второе уравнение (у1®у2®у3) будет иметь тоже 5 решений. Совместное решение первого и второго уравнений имело бы 25 решений (по 5 решений для у на каждое решение для х), но опять надо учитывать третье уравнение (х1®у1 =1): нам нужны только такие комбинации, где не будет сочетаний х1=1, у1=0:
| х1 | х2 | х3 | у1 | у2 | у3 | х1®у1 |
Два случая, когда х1=0, дали по 5 решений (число единичных решений х1®х2®х3=1) каждое, 3 случая х1=1 – по три решения (число нулевых решений х1®х2®х3=1).
Число решений 2*5+3*3=19.
Таким образом, закономерность уже выстраивается:
Для системы
х1®х2 =1
у1®у2 =1
х1®у1=1
базовое уравнение х1®х2 имеет 3 единичных и 1 нулевое решение, из единичных решений в 2 случаях х1=0, в одном х1=1. Число решений 2*3+1*1=7
((число решений с х1=0 (2)* число единичных решений базового уравнения (3)) + (число решений с х1=1 (1) * число нулевых решений базового уравнения (1))).
Для системы
х1®х2 ®х3 =1
у1®у2®у3 =1
х1®у1=1
базовое уравнение х1®х2 ®х3 имеет 5 единичных решений (3 единичных решения аргумента х1®х2 дают по одному решению, одно нулевое по два решения) и 3 нулевых. Из единичных решений 3 получены при х1=1 (от 3 решений х1®х2) и два оставшихся при х1=0.
Число решений 2*5+3*3=19 ((число решений с х1=0 (2)* число единичных решений базового уравнения (5)) + (число решений с х1=1 (3) * число нулевых решений базового уравнения (3))).
Для системы
х1®х2 ®х3 ®х4 =1
у1®у2®у3®у4 =1
х1®у1=1
базовое уравнение х1®х2 ®х3®х4 имеет 11 единичных решений (5 единичных решений аргумента х1®х2®х3 дают по одному решению, 3 нулевых по два решения) и 5 нулевых. Из единичных решений 5 получены при х1=1 (от 5 решений х1®х2®х3) и 6 оставшихся при х1=0.
Число решений 6*11+5*5=91 ((число решений с х1=0 (6)* число единичных решений базового уравнения (11)) + (число решений с х1=1 (5) * число нулевых решений базового уравнения (5))).
Для системы
х1®х2 ®х3 ®х4 ®х5 =1
у1®у2®у3®у4 ®у5 =1
х1®у1=1
базовое уравнение х1®х2 ®х3®х4 ®х5 имеет 21 единичное решение (11 единичных решения аргумента х1®х2®х3®х4 дают по одному решению, 5 нулевых по два решения) и 11 нулевых. Из единичных решений 11 получены при х1=1 (от 11 решений х1®х2®х3®х4) и 10 оставшихся при х1=0.
Число решений 10*21+11*11=331 ((число решений с х1=0 (10)* число единичных решений базового уравнения (21)) + (число решений с х1=1 (11) * число нулевых решений базового уравнения (11))).
Для системы
х1®х2 ®х3 ®х4 ®х5 ®х6 =1
у1®у2®у3®у4 ®у5®у6 =1
х1®у1=1
базовое уравнение х1®х2 ®х3®х4 ®х5®х6 имеет 43 единичных решения (21 единичное решение аргумента х1®х2®х3®х4®х5 дают по одному решению, 11 нулевых по два решения) и 21 нулевых. Из единичных решений 21 получены при х1=1 (от 21 решения х1®х2®х3®х4®х5) и 22 оставшихся при х1=0.
Число решений 22*43+21*21=1387 ((число решений с х1=0 (22)* число единичных решений базового уравнения (43)) + (число решений с х1=1 (21) * число нулевых решений базового уравнения (21))).
Можно свести эти решения в таблицу (см. на следующей странице):
| Базовое уравнение | Число единичных решений | Число нулевых решений | Число единичных решений, полученных при х1=0 | Число единичных решений, полученных при х1=1 | Число решений системы |
| х1®х2 =1 |    3 3
| 2*3+1*1=7 | |||
| х1®х2 ®х3 =1 |    3+2*1=5 3+2*1=5
| 3 (23-5=3) | 2 (5-3=2) | 2*5+3*3=19 | |
| х1®х2 ®х3 ®х4 =1 |    5+2*3=11 5+2*3=11
| 5 (24-11) | 6 (11-5) | 6*11+5*5=91 | |
| х1®х2 ®х3 ®х4 ®х5 =1 |    11+2*5=21 11+2*5=21
| 11 (25-11) | 10 (21-11) | 10*21+11*11=331 | |
| х1®х2 ®х3 ®х4 ®х5 ®х6 =1 | 21+2*11=43 | 21 (26-43) | 22 (43-21) | 22*43+21*21= =1387 |
Пример (задание 23 демовариант 2015). Сколько существует различных наборов значений логических переменных x1, x2, … x8, y1, y2, … y8, которые удовлетворяют всем перечисленным ниже условиям?
(x1 \/ x2) /\ ((x1 /\ x2) → x3) /\ (x1 \/ y1) = 1 (1)
(x2 \/ x3) /\ ((x2 /\ x3) → x4) /\ (x2 \/ y2) = 1 (2)
… …
(x6 \/ x7) /\ ((x6 /\ x7) → x8) /\ (x6 \/ y6) = 1 (6)
(x7 \/ x8) /\ (x7 \/ y7) = 1 (7)
(x8 \/ y8) = 1 (8)
Решение. Для переменных x1, x2, … x8, y1, y2, … y8 существует 216 различных комбинаций.
Прежде всего, надо попытаться выделить общие особенности приведенных уравнений. Например, уравнения (1)-(6) однотипны. Кроме того, комбинации вида (xi \/ yi), или xi ® yi, встречаются во всех уравнениях. Уравнения (1)-(6) не связаны друг с другом переменными у, поэтому для начала попытается найти решения для переменных х.
В цепочке (векторе) x1, x2, … x8 существует 28=256 различных комбинаций значений переменных, но далеко не все они являются решениями системы.
Так, поскольку скобки в уравнениях связаны операцией И, то для того чтобы логическое выражение было истинно, все логические сомножители тоже должны быть истинными:
xiÚxi+1=1
xixi+1®xi+2=1
xi®yi=1
Из выражения xiÚxi+1=1 следует, что комбинации xi=0, xi+1=0 недопустимы, т.к. в таком случае xiÚxi+1=0.
Из выражения xixi+1®xi+2=1 следует, что недопустимы также комбинации
xi =1, xi+1=1, xi+2=0.
Получается, что можно сразу исключить набор значений х, состоящий только из нулей, а также любые наборы, в которых есть два нуля, идущих подряд, или две единицы и ноль. Таких наборов немного – это все единицы, а также такие цепочки, где чередуются единицы и нули:
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 |
Каждый из таких наборов можно комбинировать только с такими наборами у, которые соответствуют условию xi®yi=1, т.е. следует исключить сочетания xi=1, yi=0.
Например, вектор х
1 1 1 1 1 1 1 1
можно скомбинировать только с таким же вектором у
1 1 1 1 1 1 1 1
Вектор х
0 1 1 1 1 1 1 1
комбинируется уже с двумя векторами у
0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
т.к. при х1=0 у1 может быть равен как 0, так и 1.
Вектор х
1 0 1 1 1 1 1 1
также комбинируется с двумя векторами у
1 0 1 1 1 1 1 1
1 1 1 1 1 1 1 1
т.к. при х2=0 у2 может быть равен как 0, так и 1.
Вектор х
0 1 0 1 1 1 1 1
комбинируется с четырьмя векторами у
0 1 0 1 1 1 1 1
0 1 1 1 1 1 1 1
1 1 0 1 1 1 1 1
1 1 1 1 1 1 1 1
т.к. при х1=0 у1 может быть равен как 0, так и 1, аналогично для х3 и у3.
Устанавливается закономерность:
для набора х 11111111 подходит 1 набор у
для набора х 01111111 подходит 2 набора у
для набора х 10111111 подходит 2 набора у
для набора х 01011111 подходит 4 набора у
для набора х 10101111 подходит 4 набора у
для набора х 01010111 подходит 8 наборов у …
для набора х 10101011 подходит 8 наборов у
для набора х 01010101 подходит 16 наборов у
для набора х 10101010 подходит 16 наборов у
Всего в сумме получается61набор.
Осталась одна неучтенная комбинация из уравнения (7)
x7 \/ x8=1, однако, поскольку комбинации x7=0 и x8=0 исключены из рассмотрения, остается 61 вариант.
Дата добавления: 2015-01-29; просмотров: 332; Мы поможем в написании вашей работы!; Нарушение авторских прав |