ЛІТЕРАТУРА ДОДАТКОВА

1. Визначення головних моментів інерції складних перерізів

можна запропонувати такий порядок обчислення головних моментів інерції складних фігур, що мають вісь симетрії.

Приклад 1. Обчислити головні моменти інерції тавра /рис.12/.

Розв'язання. Розбиваємо тавр на два простих прямокутники. Перший прямокутник площею А1 = 6а•2а = 12а² має центр ваги в точці С₁, його центральні осі позначимо z₁ і y_1. Відносно цих осей, користу­ючись формулами , визначимо осьові моменти інерції пря­мокутника:

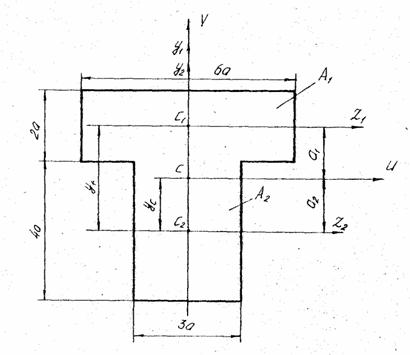
Рис. 12. Схема до обчислення моментів інерції складної площі поперечного перерізу.Другий прямокутник має площу А₂ = 4а •3а = 12а² , його центр ваги - С₂ і центральні осі z₂ ,y₂ .Центральні моменти інерції другого прямокутника

За одну з головних центральних осей інерції V беремо вісь си­метрії тавра. Оскільки осі у₁ і у₂ збігаються з головною віссю V, то момент інерції тавра відносно осі V буде

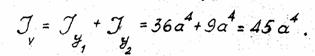
Для визначення положення головної центральної осі u встановимо центр ваги тавра С. За допоміжну систему координат візьмемо осі V і Z₂ . Тоді ордината центра ваги фігури

Абсциса центра ваги площі фігури розміщена на центральній осі V . Визначене таким чином положення центра ваги С показано на рис.12. Провівши через точку С пряму, перпендикулярну до осі симетрії, ма­тимемо другу головну центральну вісь U.

Позначимо відстані від осі U до паралельних їй осей z₁ і z₂ відповідно через а₁ та а_2. Головний центральний момент інер­ції тавра відносно осі U визначаємо за формулою І_u^І = I_u^I + I_u^II, де I_u^I і I_u^II - моменти інерції від­повідно першого і другого прямокутника відносно осі U. Використовую­чи формулу /5.16/, дістаємо