
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Экстремум функции двух независимых переменных
Функция z = f(x, у) имеет максимум (минимум)в точке 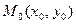 , если значение функции в этой точке является наибольшим (наименьшим) по сравнению с другими значениями функции из окрестности точки
, если значение функции в этой точке является наибольшим (наименьшим) по сравнению с другими значениями функции из окрестности точки 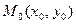 .
.
Максимумы и минимумы функции называются экстремумами,а точка 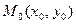 – экстремальной точкой.
– экстремальной точкой.
Теорема(необходимые условия экстремума). Если z = f(x, у) дифференцируемая функция и достигает в точке М0(х0, у0) экстремума, то ее частные производные первого порядка в этой точке равны нулю:
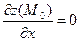 ,
, 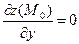 .
.
Точки, в которых частные производные первого порядка обращаются в нуль (или не существуют), называются критическимиили стационарными. Исследование их на экстремум проводят с помощью достаточных условий существования экстремума функции двух переменных.
Пусть 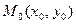 – стационарная точка функции z= f(x, у). Для ее исследования сначала вычисляют частные производные второго порядка в точке
– стационарная точка функции z= f(x, у). Для ее исследования сначала вычисляют частные производные второго порядка в точке 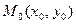 :
:
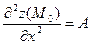 ;
; 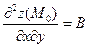 ;
; 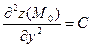 ,
,
а затем дискриминант 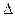 = АС — В2. Тогда достаточные условия экстремумафункции z = f(x, у) в стационарной точке М0(х0, у0) запишутся в следующем виде:
= АС — В2. Тогда достаточные условия экстремумафункции z = f(x, у) в стационарной точке М0(х0, у0) запишутся в следующем виде:
1) 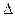 >0 – экстремум есть, при этом, если А>0 (или С>0 при А=0) в точке
>0 – экстремум есть, при этом, если А>0 (или С>0 при А=0) в точке 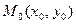 функция имеет минимум, а если А<0 (или С<0 при А = 0) – максимум;
функция имеет минимум, а если А<0 (или С<0 при А = 0) – максимум;
2) 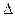 < 0 – экстремума нет;
< 0 – экстремума нет;
3) 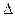 = 0 – требуются дополнительные исследования.
= 0 – требуются дополнительные исследования.
Дата добавления: 2015-02-10; просмотров: 151; Мы поможем в написании вашей работы!; Нарушение авторских прав |