Формула полной вероятности.

Предположим теперь, что событие В может осуществиться с одним и только с одним из n несовместимых событий . Иными словами, положим , где события BA_i и BA_j с разными индексами i и j несовместимы. По теореме сложения вероятностей имеем: .

Применяя теорему умножения, находим:

(1.8.1)

Это равенство носит название формулы полной вероятности и играет важную роль во всей дальнейшей теории.

В качестве иллюстрации рассмотрим два примера.

Пример 1. Имеется пять урн:

2 урны состава A₁ — по два белых шара и одному черному,

1 урна состава A₂—по 10 черных шаров,

2 урны состава A₃ — по три белых шара и одному черному.

Наудачу выбирается урна и из нее наудачу вынимается шар. Чему равна вероятность, что вынутый шар белый (событие В)?

Так как вынутый шар может быть только из урны 1-го, 2-го или 3-го состава, то .

По формуле полной вероятности

Но

Таким образом, .

Пример 2. Известно, что вероятность поступления k вызовов на телефонную станцию за промежуток времени t равна .

Считая, что появление какого-либо числа вызовов за два соседних промежутка времени являются событиями независимыми, найти вероятность поступления s вызовов за промежуток времени длительности 2t.

Решение. Обозначим через событие, состоящее в поступлении k вызовов за время . Очевидно, что мы имеем следующее равенство: , которое означает, что событие можно рассматривать как сумму s+1 несовместимых событий, состоящих в том, что за первый промежуток времени длительности t поступает i вызовов, а за следующий промежуток той же продолжительности — поступает s — i вызовов .

По теореме сложения вероятностей

По теореме умножения вероятностей для независимых событий

Таким образом, если положить 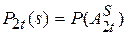, то .

Впоследствии мы увидим, что при некоторых весьма общих условиях . , где а — некоторая константа.

находим:

Но

Поэтому

Для промежутков времени, в два раза больших, и, как легко убедиться, для любых кратных t промежутков времени характер формулы для вероятности сохраняется.