Числовые характеристики системы нескольких случайных величин.

Закон распределения системы (заданный функцией распределения или плотностью распределения) является полной, исчерпывающей характеристикой системы нескольких случайных величин. Иногда ограниченность экспериментального материала не дает возможности построить закон распределения системы. В других случаях исследование вопроса с помощью сравнительно громоздкого аппарата законов распределения не оправдывает себя в связи с не­высокими требованиями к точности результата.

Во всех таких случаях вместо законов распределения применяют неполное, приближенное описание системы случайных величин с по­мощью минимального количества числовых характеристик.

Минимальное число характеристик, с помощью которых может быть охарактеризована система п случайных величин , сводится к следующему:

1) вектор математических ожиданий:

(5.8.1)

характеризующий средние значения компонент;

Здесь

2) вектор дисперсий

(5.8.2)

характеризующий рассеивание компонент;

Здесь

3) корреляционных моментов

где

характеризующих по парную корреляцию всех величин, входящих в систему.

Заметим, что дисперсия каждой из случайных величин Х_i есть, по существу, не что иное, как частный случай корреля­ционного момента, а именно:

(5.8.3)

Все корреляционные моменты и дисперсии удобно расположить в виде прямоугольной таблицы (называемой матрицей):

(5.8.4)

Эта таблица называется корреляционной матрицей системы слу­чайных величин .

Очевидно, что не все члены корреляционной матрицы различны. Из определения корреляционного момента ясно, что , т. е. элементы корреляционной матрицы, расположенные симме­трично по отношению к главной диагонали, равны. В связи с этим часто заполняется не вся корреляционная матрица, а лишь ее половина, считая от главной диагонали:

(5.8.5)

Корреляционную матрицу, составленную из элементов , часто сокращенно обозначают символом .

По главной диагонали корреляционной матрицы стоят дисперсии случайных величин .

В случае, когда случайные величины некоррелированны, все элементы корреляционной матрицы, кроме диагональ­ных, равны нулю:

Такая матрица называется диагональной.

В целях наглядности суждения именно о коррелированности случайных величин пользуются нормированной корреляционной матрицей , составленной не из корреляцион­ных моментов, а из коэффициентов корреляции: ; .

Все диагональные элементы этой матрицы, естественно, равны единице. Нормированная корреляционная матрица имеет вид:

(5.8.6)

Введем понятие о некоррелированных системах случайных величин. Рассмотрим две системы случайных величин: ; 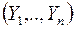или два случайных вектора в n-мерном пространстве: X с составляющими и Y с составляющими .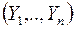

Случайные векторы X и Y называются некоррелированными, если каждая из составляющих вектора X некоррелированная с каждой из составляющих вектора Y: