Находим определитель матрицы.

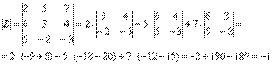
Здесь определитель раскрыт по первой строке.

Также не забываем, что 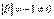, а значит, всё нормально – обратная матрица существует.

2) Находим матрицу миноров .

Матрица миноров имеет размерность «три на три» , и нам нужно найти девять чисел.

Я подробно рассмотрю парочку миноров:

Рассмотрим следующий элемент матрицы:

МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

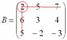
Оставшиеся четыре числа записываем в определитель «два на два»

Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить:

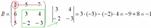
Всё, минор найден, записываем его в нашу матрицу миноров:

Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.

Ну и для закрепления – нахождение еще одного минора в картинках:

Остальные миноры попробуйте вычислить самостоятельно.

Окончательный результат:
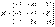– матрица миноров соответствующих элементов матрицы .

То, что все миноры получились отрицательными – чистая случайность.

3) Находим матрицу алгебраических дополнений .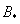

В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов:

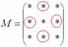
В данном случае:
– матрица алгебраических дополнений соответствующих элементов матрицы B.

4) Находим транспонированную матрицу алгебраических дополнений .

– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы B.

5) Ответ:

32. Решение матричного уравнения А·Х = В, если det А ≠ 0?

Рассмотрим матричное уравнение вида А·Х = В, где А – невырожденная квадратная матрица порядка m, В – матрица размера m*р, А и В – известные матрицы. Чтобы найти неизвестную матрицу Х размера m*р умножим обе части матричного уравнения слева на матрицу А^-1 – обратную к матрице А: А^-1 ·А·Х = А^-1·В. Учитывая, что А^-1·А = Е, где Е –единичная матрица порядка m, получим решение матричного уравнения:

Х = А^-1·В.

33. Решение матричного уравнения Y·А = В, если det А ≠ 0?

При решении матричного уравнения вида Х·А = В, в котором А – известная невырожденная квадратная матрица порядка m, В –известная матрица размера р* m, умножают обе части матричного уравнения справа на матрицу А^-1 – обратную к матрице А: Х·А· А^-1 = В· А^-1, после чего получают решение:

Х = В·А^-1.

34. Определение арифметического вектора.

Арифметическим вектором называется упорядоченная совокупность n чисел. Обозначается , числа называются компонентами арифметического вектора.

Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: ,

для любых 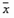и 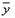и любого числа

35. Операции над арифметическими векторами.

Для любых , , 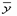из Rⁿ и любых чисел a, b справедливо:

1. 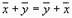, сложение коммутативно;

2. ,сложение ассоциативно;

3.

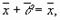
4.

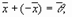
5. , умножение на число ассоциативно;

6. ;

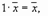7. 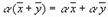, умножение на число дистрибутивно относительно сложения элементов;

8. 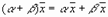, умножение вектора на число дистрибутивно относительно сложения чисел.

36. Определение ортогональных векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю. a · b = 0

37. Определение линейной комбинации векторов.

Линейной комбинацией векторов a₁, ..., a_n с коэффициентами x₁, ..., x_n называется вектор: x₁a₁ + ... + x_na_n.

38. Определение линейно зависимой и линейно независимой систем векторов.

Вектора a₁, ..., a_n называются линейно независимыми, если не существует нетривиальной комбинации этих векторов равной нулевому вектору. Tоесть вектора a₁, ..., a_n линейно независимы если x₁a₁ + ... + x_na_n = 0 тогда и только тогда, когда x₁ = 0, ..., x_n = 0.

Вектора a₁, ..., a_n называются линейно зависимыми, если существует нетривиальной комбинации этих векторов равная нулевому вектору.

39. Теорема о необходимом и достаточном условии линейной зависимости системы векторов.

Теорема: Для того чтобы система векторов линейного пространства была линейно зависимой необходимо и достаточно, чтобы какой-нибудь вектор этой системы был линейной комбинацией всех остальных.
Доказательство:Дана линейно зависимая система. Нужно доказать, что один вектор линейной комбинации всех остальных.

а_1, а_2, а_{3, …} а_n – ЛЗ система векторов, т.е. среди α_1, α₂ ,α₃ … α_n существует число отличное от нуля так, что ЛК α₁а₁+ α₂ а₂+α₃ а₃+…+ α_n а_n= 0.

Положим для определения, что коэффициент α₁ ≠ 0. Разделим обе части последнего равенства на α₁ ≠ 0:

Отсюда следует, что а₁ - ЛК остальных векторов.