Постановка задачи численного интегрирования. Формулы прямоугольников. Двойной пересчет.

При решении многих задач возникает необходимость вычисления определенных интегралов. Пусть требуется вычислить интеграл. Если для подынтегральной функции f(x) найдена первообразная F(x), то интеграл можно вычислить по формуле Ньютона-Лейбница: .

Однако, часто не бывает возможности использовать эту формулу, например, в следующих случаях:

1) Если первообразная функция F(x) не выражается в конечном виде через элементарные функции, так называемые не берущиеся интегралы:

2) Если первообразная функция F(x) имеет настолько сложную аналитическую запись, что ее использование не целесообразно.

3) Если подынтегральная функция f(x) задана графически или таблично.

Во всех этих случаях возникает необходимость разработки методов, позволяющих вычислять определенные интегралы приближенно. Эти формулы для вычисления приближенных интегралов называются квадратными.

Вывод формул прямоугольников основан на замене определенного интеграла интегральной суммы. Из курса мат анализа известно, что , где - интегральная сумма для функции f(x) на промежутке [a;b]. Точка - производная точка, принадлежащая отрезку .

Если отрезок [a;b] разбить на n - равных частей, тогда любое . В этом случае, h - шаг квадратурной формулы, при этом условии, .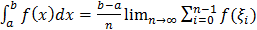

Если в качестве точек взять левые концы частичных отрезков, то есть , где 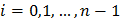, то получим:

Эта формула называется формулой левых прямоугольников.

Если в качестве точек взять правые концы частичных отрезков, то получим частичный интеграл.

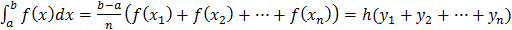- формулу правых прямоугольников.

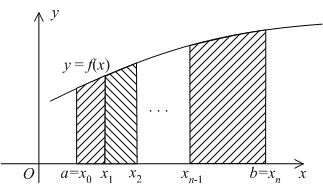
Очевидно, что формула прямоугольников тем точнее, чем больше h.

Абсолютная погрешность формулы прямоугольников оценивается следующим образом: где М₁ – максимум модуля от первой производной подынтегральной функции на отрезке [a,b].