
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формула Байеса.
Ответ: Эта формула применяется при решении практических задач, когда событие 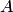 , появляющееся совместно с каким-либо из событий
, появляющееся совместно с каким-либо из событий 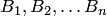 , образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез
, образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез 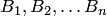 . Априорные (до опыта) вероятности
. Априорные (до опыта) вероятности  известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности
известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности  . Для гипотезы
. Для гипотезы  формула Байеса выглядит так:
формула Байеса выглядит так:  Раскрывая в этом равенстве
Раскрывая в этом равенстве  по формуле полной вероятности (2.1), получаем:
по формуле полной вероятности (2.1), получаем:
 Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный. Решение. Рассчитаем условные вероятности по формуле Байеса:
Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный. Решение. Рассчитаем условные вероятности по формуле Байеса:
для первого станка 
для второго станка 
для третьего станка 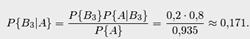
Дата добавления: 2015-01-19; просмотров: 136; Мы поможем в написании вашей работы!; Нарушение авторских прав |