КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Комплексная экспонента. Формула Эйнера.
Ответ:
| Формула Эйлера для комплексной экспоненты: |
| Формула, связывающие показательную и тригонометрическую функции eiz = cos z + i sin z , где z – произвольное комплексное число, а i – единица мнимая, называется формулой Эйлера для комплексной экспоненты. Из нее вытекают два других тождества: cos z = (eiz + e-iz) / 2, sin z = (eiz - e-iz) / 2i. |
Экспоне́нта (комплексного переменного) — математическая функция, задаваемая соотношением f(z) = ez, где z есть комплексное число.
Вообще говоря, такое определение формально и не имеет достаточной строгости. Поэтому более точно экспонента определяется как аналитическое продолжение экспоненты f(x) = ex вещественного переменного x. Определим формальное выражение: 
.
Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность
функции ez, т.е. показать, что ez разлагается в некоторый сходящийся к данной функции ряд. Покажем это:
Сходимость данного ряда легко доказывается: 
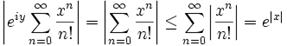. Ряд всюду сходится абсолютно, т.е. вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции f(z) = ez. Согласно теореме единственности, полученное продолжение будет единственно, следовательно, функция ez является аналитической и определенной. Комплексная экспонента, в отличие от экспоненты вещественного переменного, периодична. Из формулы Эйлера следует, что
. Отметим, кроме того, что функция ez имеем чисто мнимый предел. Из периодичности комплексной экспоненты следует, что максимальной областьюоднолистности будет горизонтальная полоса на комплексной плоскости 
Дата добавления: 2015-01-19; просмотров: 243; Мы поможем в написании вашей работы!; Нарушение авторских прав |