Численные методы решения нелинейных уравнений. Постановка задачи. Уточнение корня методом хорд

В общем случае нелин. уравнения с одной переменной можно записать так: F(x)=0 (1), где F(x) определена и непрерывна на некотором отрезке [a,b]. Всякое число α, обращающее F(x) в 0, называется корнем уравнения (1).

Метод хорд

Пусть корень уравнения (1) отделен на отрезке [a,b]. Требуется уточнить корень х* с точностью ε>0.

Метод основан на замене функции f(x) на каждом шаге поиска хордой, проходящей через точки с координатами (a; F(a)), (b; F(b)).

Обозначим точку пересечения хорды с осью ОХ с₁ и запишем уравнение хорды как уравнение прямой

Так как точка с координатами (c₁; 0) принадлежит хорде, то ее координаты удовлетворяют уравнению хорды

Отсюда выражаем с₁, получаем

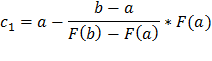
Полученная формула называется формулой метода хорд, а с₁ – первым приближением к х*. Очевидно, что теперь корень уравнения (1) находится на отрезке [c₁;b]. Продолжая указанный выше процесс, получаем рекуррентную формулу метода хорд:

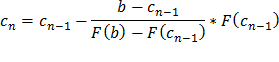
Последовательность с₁,с₂,…,с_n,… сходится к х*, если функция F(x) имеет знакопостоянные первую и вторую производные на отрезке [a,b].

В данной серии формул метода хорд приближение строится с конца а, при этом конец b остается неподвижен. Однако может возникнуть ситуация, когда неподвижным является конец а, а приближение строится с b. Тогда формулы будут иметь следующий вид:

…

Очевидно, что в формулах метода хорд неподвижным является тот конец, в котором знаки функции и ее второй производной совпадают на промежутке.

Вычисление следует заканчивать, как только расстояние между двумя соседними приближениями станет <ε, т.е. |c_n-c_n-1|≤ε.