Ускорение точек тела при сферическом движении.

Рис. 42.

Ускорение любой точки M тела, движущегося сферически, определяется формулой Ривальса и равно векторной сумме двух составляющих: вращательного и осестремительного ускорений: .

Вращательное ускорениеточки M равно векторному произведению вектора углового ускорения тела на радиус-вектор , соединяющий неподвижную точку тела с точкой M (20): .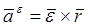

Осестремительное ускорениеточки M равно векторному произведению вектора угловой скорости 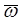тела на вектор вращательной скорости точки M (21): .

Вектор вращательного ускорения 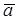^e точки M тела, движущегося сферически, направлен перпендикулярно мгновенной оси ускорения тела и прямой, соединяющей точку M с осью E.

Величина вращательного ускорения точки M тела, движущегося сферически, равна произведению углового ускорения тела на расстояние от точки до мгновенной оси ускорения: . (рис. 42).

Вектор осестремительного ускорения 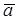^w точки M тела, движущегося сферически, направлен от точки M к мгновенной оси вращения W.

Величина осестремительного ускорения точки M тела, движущегося сферически, равна произведению квадрата угловой скорости тела на расстояние от точки до мгновенной оси вращения: . (рис. 42).

Дата добавления: 2015-04-15; просмотров: 33; Нарушение авторских прав