Задания.

1) Сколько различных решений имеет уравнение

((J → K) →(M Ù N Ù L)) Ù ((M Ù N Ù L) → (J Ú K)) Ù (M → J) = 1

где J, K, L, M, N – логические переменные?

2) Сколько существует различных наборов значений логических переменных x1, x2, ... x9, x10, которые удовлетворяют всем перечисленным ниже условиям?

((x1 ≡ x2) \/ (x3 ≡ x4)) /\ ((x1 ≡ x2) \/ (x3 ≡ x4)) =1

((x3 ≡ x4) \/ (x5 ≡ x6)) /\ ((x3 ≡ x4) \/ (x5 ≡ x6)) =1

...

((x7 ≡ x8) \/ (x9 ≡ x10)) /\ ((x7 ≡ x8) \/ (x9 ≡ x10)) =1

3) Упростить логическую формулу:

4) Упростить логическую формулу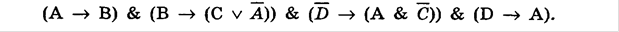

5) Указать значения X,Y,Z,T, при которых логическое выражение ложно

Ø(XÚØY)®(XÚØZÚØT).

6) A,B,C – целые числа, для которых истинно высказывание

(C-1<B)Ù(C-1<=ÚC>B)Ù(C>A)

Чему равно С, если А=5, В=10?

7) Сколько решений имеет система уравнений (+ - ИЛИ, ! – НЕ, & - И)

((A=B)+(C=D))&(!(A=B)+!(C=D))=1

((A=C)+(D=E))&(!(A=C)+!(D=E))=1

((A=D)+(E=F))&(!(A=D)+!(E=F))=1

((A=E)+(F=G))&(!(A=E)+!(F=G))=1

8) Сколько решений имеет система уравнений

(!(A=B)+(C=D))&((A=B)+!(C=D))=1

(!(A=C)+(D=E))&((A=C)+!(D=E))=1

(!(A=D)+(E=F))&((A=D)+!(E=F))=1

(!(A=E)+(F=G))&((A=E)+!(F=G))=1

A=E=1

9) Сколько решений имеет система уравнений

((A=D)+(C=D))&((A=B)->(C=D))=1

((A=E)+(D=E))&((A=C)->(D=E))=1

((A=F)+(E=F))&((A=D)->(E=F))=1

((A=G)+(F=G))&((A=E)->(F=G))=1

((A=H)+(G=H))&((A=F)->(G=H))=1

10) Сколько различных решений имеет система уравнений?

(x₁ ® x₂)Ù(x₂ ® x₃)Ù(x₃ ® x₄)Ù(x₄ ® x₅) = 1

(у₁ ® у₂)Ù(у₂ ® у₃)Ù(у₃ ® у₄)Ù(у₄ ® у₅) = 1

x₁ Ú у₁ = 1

11) Сколько различных решений имеет система уравнений?

(x₁ ® x₂) Ú x₃ Ù Øx₄ = 1

(x₃ ® x₄) Ú x₅ Ù Øx₆ = 1

(x₅ ® x₆) Ú x₇ Ù Øx₈ = 1

(x₇ ® x₈) Ú x₉ Ù Øx₁₀ = 1

(x₉ ® x₁₀) Ú x₁ Ù Øx₂ = 1

где x₁,x₂,…,x₁₀ – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

12) Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, х2, х3, х4, х5, х6, х7, х8, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1®х2) ® (х3®х4) = 1

(х3®х4) ® (х5®х6) = 1

(х5®х6) ® (х7®х8) = 1

13) Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, x₂, ... x₈, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x₁ ≡ x₂) ∧ ( (x₁ ∧ x₃) ∨ (x₁ ∧ x₃) ) = 0

(x₂ ≡ x₃) ∧ ( (x₂ ∧ x₄) ∨ (x₂ ∧ x₄) ) = 0

...

(x₆ ≡ x₇) ∧ ( (x₆ ∧ x₈) ∨ (x₆ ∧ x₈) ) = 0

14) Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, x₂, ... x₁₀, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x₁ ≡ x₂) ∧ (x₁ ∨ x₃) ∧ (x₁ ∨ x₃) = 0

(x₂ ≡ x₃) ∧ (x₂ ∨ x₄) ∧ (x₂ ∨ x₄) = 0

...

(x₈ ≡ x₉) ∧ (x₈ ∨ x₁₀) ∧ (x₈ ∨ x₁₀) = 0

15) Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, x₂, x₃, x₄, y₁, y₂, y₃, y₄, z₁, z₂, z₃, z₄, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1→x2) ∧ (x2→x3) ∧ (x3→x4) = 1

(x1 ∧ y1 ∧ z1) ∨ (x1 ∧ y1 ∧ z1) ∨ (x1 ∧ y1 ∧ z1) = 1

(x2 ∧ y2 ∧ z2) ∨ (x2 ∧ y2 ∧ z2) ∨ (x2 ∧ y2 ∧ z2) = 1

(x3 ∧ y3 ∧ z3) ∨ (x3 ∧ y3 ∧ z3) ∨ (x3 ∧ y3 ∧ z3) = 1

(x4 ∧ y4 ∧ z4) ∨ (x4 ∧ y4 ∧ z4) ∨ (x4 ∧ y4 ∧ z4) = 1

16) Сколь­ко раз­лич­ных ре­ше­ний имеет си­сте­ма урав­не­ний

x1 ∨ x2 = 1

x2 ∨ x3 = 1

…

x9 ∨ x10 = 1,

где x1, x2, … x10 — ло­ги­че­ские пе­ре­мен­ные?

Ответы.

1) 8 2) 64 3) В\/АС 4) ABCD 5) 0111 6) 6

7) 8 8) 4 9) 26 10) 11 11) 244 12) 121

13) 16 14) 20 15) 31 16) 11