Иллюстрация возникновения разных математических задач

К лекциям 1-2. Математическое моделирование электрических схем

Введение

Обобщенно можно сказать, что физики и инженеры рассматривают процессы (явления) либо для их изучения, либо для создания новых конструкций и приборов.

Для обеих целей важнейшим этапом рассмотрения является эксперимент. Без него нельзя обойтись. Но можно несколько облегчить задачу изучения процессов созданием адекватной математической модели явления или конструкции.

Этапы эксперимента

1. Создание экспериментальной установки (конструкции).
2. Изменение параметров при проведении эксперимента
3. Выделение процессов, играющих основную роль в рассматриваемой области параметров.

Этапы математического моделирования

1. Построение математической модели на основе знаний об элементарных физических (химических, биологических, …) процессах, играющих основную роль в наблюдаемых явлениях.
2. Приведение модели к набору стандартных математических задач. При этом используется библиотека стандартных задач, известных исследователям.
3. Уточнение условий, когда рассматриваемые задачи имеют решения и когда оно единственно.
4. Выбор алгоритма решения.
5. Получение, если возможно, аналитическое решение.
6. Получение численных решений.

Иллюстрация возникновения разных математических задач

Рассмотрим задачи, которые возникают при математическом моделировании электрической схемы, представленной на рис. 1. Оказывается, что в зависимости от предположений о заданной зависимости ЭДС от времени можно получить разные математические задачи.

Рис.1 Схема, содержащая два ключа , два источника ЭДС E1, E2, семь сопротивлений R1-R7 и два конденсатора емкостью C1, C2.

В рассматриваемой схеме существуют три узловые точки (жирные точки на рис.1), в которых число входящих и исходящих токов больше двух. Мы обозначили потенциалы в этих точках буквами ф0, ф1, ф2. Необходимо написать соотношения между разностями этих потенциалов и протекающими токами по всем возможным путям прохождения тока между узловыми точками (что эквивалентно второму закону Кирхгофа).

Напомним факты, известные из курса физики. Ток 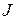, протекающий через сопротивление , связан с разностью потенциалов 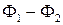на концах сопротивления соотношением 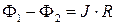. Связь между током и разностью потенциалов на обкладках конденсатора более сложная и представлена на рис 2.

Рис. 2. Процесс зарядки конденсатора. Связь между током, зарядом и разностью потенциалов на обкладках конденсатора.

При рассмотрение электрических схем можно произвольно вводить неизвестные токи. Надо только придерживаться следующих правил.

1. Количество токов должно соответствовать числу независимых замкнутых ячеек схемы.
2. В каждой узловой точки сумма входящих и выходящих токов (с учетом знаков) должна равняться нулю (первый закон Кирхгофа).

На рис1. мы воспользовались тремя токами (по числу трех независимых контуров), обозначенных (нумерация привязана для удобства к номерам соответствующих сопротивлений, по которым эти токи протекают).

Нетрудно заметить, что между потенциалами ф0 и ф1 существуют два пути для токов . Для этих путей связь между разностью потенциалов и токами выражаются уравнениями (1), (2). Между узловыми точками с потенциалами ф1 и ф2 существует лишь один путь для тока , что и описывается соотношением (3). Для двух возможных путей протекания токов и между узловыми точками с потенциалами ф2 и ф0 связи между разностями потенциалов в узловых точках и протекающими токами определяются соотношениями (4), (5).

Связь между зарядами обкладок конденсатора и «протекающим» током определяются, согласно рисунку 2, дифференциальным соотношением между током и зарядом:

Таким образом, рассматриваемая электрическая схема эквивалентна системе пяти линейных алгебраических уравнений (1)-(5) и двух линейных дифференциальных уравнений (6)-(7) для семи величин: двух разностей между узловыми потенциалами (ф1-ф0), (ф2-ф0), трех токов и зарядов на обкладках двух конденсаторов.

В общем случае, когда разности потенциалов у источников ЭДС известны как заданные функции времени, то и все семь искомых величин будут также функциями времени. В этом случае если мы зададим для них начальные условия, то получим математическую задачу, известную в математике как задача Коши.

Частные случаи общей схемы, изображенной на рис. 1

Зарядка и разрядка конденсатора

Заметим, что рассматриваемая схема состоит из трех электрических контуров, устроенных одинаковым образом: ключ, источник питания, три сопротивления и один конденсатор.

Поэтому остановимся подробно на первом контуре, предполагая, что два других отключены от первого (разрыв в цепи в узле 1). Формально это означает, что мы предполагаем, что и рассматриваем первые три уравнения из системы (1)-(7) изолированно – первое, второе и шестое, присвоив им номера (8)-(10):

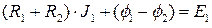, (8)

, (9)

. (10)

Сложив уравнения (8) и (9) и воспользовавшись соотношением (10), получим одно линейное дифференциальное уравнение первого порядка для заряда конденсатора:

. (11)

Уравнение (8), а следовательно и (11) подразумевают, что ключ К1 замкнут. Предположим, что до момента 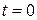ключ был разомкнут и конденсатор был разряжен. Это означает, уравнение (11) для функции , справедливое при 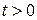, мы должны дополнить начальным (по времени) условием:

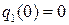. (12)

Не останавливаясь на деталях, напишем решение задачи (11)-(12) в общем случае произвольной зависимости от времени напряжения источника тока :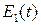

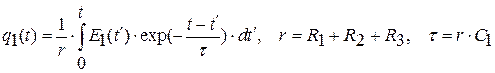. (13)

Проверка того, что функция (13) удовлетворяет уравнению (11) является простым упражнением на дифференцирование. Выполнение условия (12) очевидно.

Если напряжение 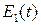остается неизменным при 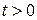( 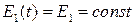), то вычисление интеграла в (13) не составляет труда, а результат принимает вид:

(14)

Интерпретация полученного результата очевидна. Включение постоянного напряжения в цепи дает начало заряду конденсатора, при котором заряд на обкладках конденсатора меняется от 0 до . Формально этот процесс заканчивается за бесконечное время, однако уже через время 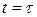заряд на конденсаторе достигает 63% от конечного, а при 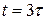он уже составляет 95% от предельного. К этому времени «проходящий через конденсатор» ток уменьшается до 5% от величины 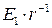в начале процесса зарядки. Поэтому физики и инженеры называют величину 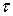характерным временем заряда конденсатора.

Что будет происходить в рассматриваемом первом контуре, если после зарядки конденсатора (т.е. через время 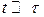) источник тока отключить и вместо него вставить бесконечно малое сопротивление?

Будем считать, что конденсатор к этому времени уже зарядился практически до величины на обкладках и это будет его начальным состоянием, т.е. вместо условия (12) будем иметь начальное условие для нового процесса:

. (15)

Поскольку теперь в контуре отсутствует источник тока, а добавление бесконечно малого сопротивления к пренебрежимо мало, то вместо уравнения (11) процесс будет описываться уравнением

. (16)

Решение этого уравнения с учетом начального условия (15) легко «угадать»:

(17)

Интерпретация этого результата также очевидна. Заряд на обкладках конденсатора быстро убывает до нуля с тем же характерным временем, что и он нарастал в предыдущей задаче, а ток скачком возрастает до величины (знак минус указывает на противоположное направление по отношению к току заряда) и также быстро стремиться к нулю.

Разобравшись с процессами зарядки и разрядки конденсаторов, можно рассмотреть всю схему на рис.1 при больших временах после включения двух источников токов с постоянными .

Статическое решение для схемы на рис. 1

Как следует из рассмотрения предыдущей задачи для одного контура, если в полной схеме на рис. 1 разности потенциалов источников тока являются неизменными во времени, то через некоторое время после включения (определяемого временами зарядки конденсаторов), заряды на конденсаторах не будут меняться и «токи через конденсаторы перестанут протекать». Другими словами можно считать, что к уравнениям (1)-(7) следует добавить условия равенства нулю левых частей уравнений (6)-(7) Эти условия приведут к тому, что

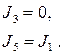(18)

В этом случае сумма уравнений (1)+(3)+(4) приводит к ожидаемому равенству

, (19)

разность узловых потенциалов определяются уравнениями (1) и (4):

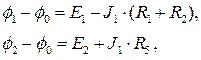(20)

а заряды конденсаторов определяются уравнениями (2) и (5):

(21)

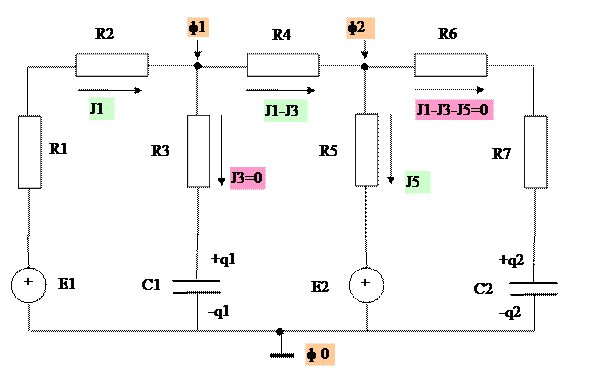Рис 3. Схема для рассмотрения статического решения при постоянных значениях E1 и E2.

Динамика зарядов на конденсаторах в общем случае уравнений (1)-(7)

Систему уравнений (1)-(7) нетрудно записать в матричном виде. Такая запись является более наглядной и позволяет легче охватить общую структуру уравнений, а также сформулировать общую постановку задачи и пути ее решения.

Введем необходимые обозначения. Объединим в один вектор две известные величины , а семь неизвестных величин представим в виде двух векторов и . В первый вектор включим два неизвестных заряда 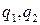и во второй вектор - оставшиеся пять неизвестных величин - три тока и две разности потенциалов:

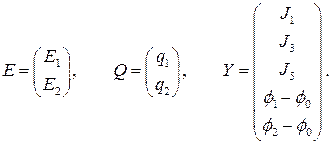(22)

Нам потребуются еще три прямоугольные матрицы, состоящие из постоянных величин и обозначенных большими греческими буквами :

одна матрица размерности 2х5

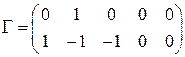, (23)

и две матрицы размерности 5х2

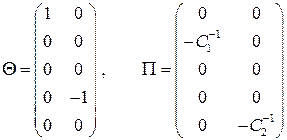. (24)

И последняя (по счету, а не по значению) из необходимых нам матриц будет квадратная матрица 5х5, определяемая левой частью уравнений (1)-(5):

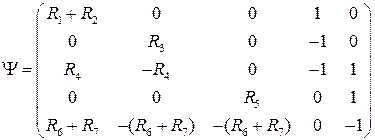. (25)

Нетрудно проверить, что с помощью введенных обозначений исходная система уравнений (1)-(7) приобретет компактный вид:

(26)

Из (26) следует, что если матрица не особая (т.е. обратима), то вся задача может быть сведена к решению системы двух линейных дифференциальных уравнений для неизвестных зарядов на обкладках двух конденсаторов:

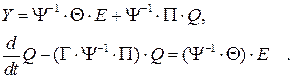(27)

С помощью MathCad можно вычислить определитель матрицы в символьном виде:

и, следовательно, в рассматриваемой задаче матрица обратима.

Заметим, что все матрицы в (27) не содержат зависящих от времени величин. Поэтому второе уравнение в (27) является неоднородным векторным дифференциальным уравнением с постоянными коэффициентами, в котором зависимость правой части от времени определяется зависимостью от времени потенциалов источников токов . Общее решение этой задачи при любых начальных условиях известно из стандартных курсов по дифференциальным уравнениям. Напомним, что определяющую роль в поведение решения вектора играют собственные значения матрицы . В дальнейшем мы обсудим методы решения подобных задач отдельно.