
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поведение замкнутых контуров в магнитном поле. Дипольный магнитный момент рамки с током.
 |
Рассмотрим замкнутый контур с током (рис.12.13), находящийся в однородном магнитном поле.
По закону Ампера на элемент контура dl действует сила

Результирующая таких сил равна

Вынося постоянные величины I и B за знак интеграла, получим

Интеграл  , поэтому F=0. Таким образом, результирующая сила, действующая на контур с током в однородном магнитном поле, равна нулю. Это справедливо для контуров любой формы при произвольном расположении относительно направления поля.
, поэтому F=0. Таким образом, результирующая сила, действующая на контур с током в однородном магнитном поле, равна нулю. Это справедливо для контуров любой формы при произвольном расположении относительно направления поля.
Определим результирующий вращательный момент, создаваемый силами Лоренца.
По определению, вращательный момент
 ,
,
где r – радиус-вектор, проведенный из точки О в точку приложения силы dF.
Результирующий момент


Возьмем точку О/, смещенную относительно точки О на отрезок b (рис.12.13).
Тогда вращательные моменты точек О и О/


Из рисунка видно, что

тогда

 |
(
 ). Следовательно, момент не зависит от выбора точки, относительно которой он берется.
). Следовательно, момент не зависит от выбора точки, относительно которой он берется.
Рассмотрим прямоугольную рамку с током I (рис. 12.14., а). Будем считать, что стороны 2-3 и 1-4 лежат в плоскостях, параллельные вектору В, а стороны 1-2 и 3-4 перпендикулярны вектору В.
Силы F2 и F4, приложенные к прямолинейным проводникам 2-3 и 4-3, численно равны

и направлены вдоль вертикальной оси рамки в противоположные стороны. Поэтому они полностью уравновешивают друг друга (рис 12.14.,а).
Силы F1 и F3, действующие на прямолинейные проводники 1-2 и 3-4, направлены (рис 12.14., б, показан вид рамки сверху) перпендикулярно плоскости рисунка и по закону Ампера численно равны
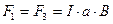
Результирующий вращающий момент М, действующий на рамку, равен моменту пары сил F1 и F3 = - F1 т.е. М = F1l, где l = b sin α.
Следовательно,
М = IabB sin α = ISB sin α,
где S = ab — площадь рамки;
Величина

называется дипольным магнитным моментом рамки с током. Направление вектора рm совпадает с направление положительной нормали к контуру.
Поэтому формулу результирующего момента можно переписать в виде
М = рm В sin α = рm B sin (рm, В).
Вращение рамки под действием пары сил F1, и F3 происходит вокруг вертикальной оси, перпендикулярной как вектору В, так и вектору рm.
На рис. 12.14., б вектор М направлен из-за чертежа перпендикулярно его плоскости.
Из формулы следует, что вектор вращающего момента, действующего на рамку с током в магнитном поле, равен векторному произведению магнитного момента рамки на магнитную индукцию внешнего поля:

Данная формула справедлива для любого плоского контура тока независимо от его формы.
Дата добавления: 2015-02-09; просмотров: 520; Мы поможем в написании вашей работы!; Нарушение авторских прав |