Оператор присваивания

Оператор присваивания имеет следующую структуру

a=b

здесь a – имя переменной или элемента массива, b - значение или выражение. В результате выполнения оператора присваивания переменной a присваивается значение выражения b.

x=5;y=sin(x);

Условный оператор

Одним из основных операторов, реализующим ветвление в большинстве языков программирования, является условный оператор if. Существует обычная и расширенная формы оператора if в Scilab. Обычный if имеет вид

IfЛогическое_выражение then

Инструкции_1

Else

Инструкции_2

End

Инструкции в списке разделяют оператором,(запятая)или ;(точка с запятой).

Логические выражения

Логические выражения состоят из констант, переменных и функций, соединенных операциями отношения: больше (>), больше или равно (>=), равно (==), не равно (~=) , меньше (<), меньше или равно (<=). Например: x²>y. Логические выражения принимают значения «истина» или «ложь». Например, при x=2 и y=8 значение выражения x²>y является ложью. Несколько логических выражений могут быть объединены в одно операторами & и |. Например: x.^2>y | y>7. Если несколько логических выражений соединены оператором &, то значение такого выражения является истиной, если каждое логическое выражение, входящее в него, является истиной. Если несколько логических выражений соединены оператором |, то значение такого выражения является истиной, если хотя бы одно логическое выражение, входящее в него, является истиной.

Зачастую при решении практических задач недостаточно выбора выполнения или невыполнения одного условия. В этом случае можно, конечно, по ветке else написать новый оператор if, но лучше воспользоваться расширенной формой оператора if.

IfЛогическое_выражение_1 then

Инструкции_1

ElseifЛогическое_выражение_2 then

Инструкции_2

Else

Инструкции_3

End

В этом случае оператор if работает так: если логическое выражение_1истинно, то выполняются инструкции_1, а затем инструкции, стоящие после оператора end. Если логическое выражение_2 является истиной, то выполняются инструкции 2, а затем инструкции, стоящие после оператора end. Если ни одно из логических выражений не является истиной, то выполняются инструкции, стоящие после слова else.

Частные случаи:

If Логическое_выражение then Инструкции , end

Примеры:

-->if x>5 then y=8, end

-->if x>5 then y=8;t=6; end

If Логическое_выражение then Инструкции_1, else Инструкции_2, end

Пример:

-->if x>5 then y=8,t=6; else y=x^2 ,end

If Логическое_выражение then

Инструкции

End

Замечание: слово thenв составе условного оператора ifне является обязательным.

Пример. Вычислить функцию y при x=0.397, если

Решение:

x=0.397;

if x.^2<=25*cos(x.^3) then

y=sin(3*x)

else

y=(2*x – tan(x))./sqrt(x.^2+2)

end

Набрав этот файл в редакторе Scipad и запустив его на выполнение командой Execute/Load into Scilab, получим:

y =

0.9287402

В качестве примера программирования разветвляющегося процесса рассмотрим решение квадратного уравнения .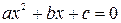

Входными данными этой задачи являются коэффициенты квадратного уравнения a, b, c. Выходными данными являются корни уравнения x1 , x2или сообщение о том, что действительных корней нет.

Алгоритм состоит из следующих этапов:

1. Ввод коэффициентов уравнения a, b и с.

2. Проверка, является ли уравнение квадратным (а≠0).

3. Вычисление дискриминанта уравнения d.

4. Если d=0, то выводится сообщение: уравнение имеет два равных корня и печатается значение корня.

5. Если d>0, определяются x1 и x2

6. Если d<0, то выводится сообщение «Корней нет».

Программа решения квадратного уравнения

clc

a=input('a=');

b=input('b=');

c=input('c=');

if a==0 then

disp("Уравнение не является квадратным")

else

// Вычисляем дискриминант.

d=b*b-4*a*c;

// Если дискриминант отрицателен,

if d<0

// то вывод сообщения,

disp(' Действительных корней нет');

elseif d==0

//иначе-вычисление корней соответствующего

// квадратного уравнения.

disp("уравнение имеет два равных корня") ;x=-b/(2*a)

else

x1=(-b+sqrt(d))/2/a

x2=(-b-sqrt(d))/2/a

end

end

a=-->1

b=-->2

c=-->-5

x1 =

1.4494897

x2 =

- 3.4494897

Найти все корни квадратного уравнения можно и без оператора if, воспользовавшись тем, что в Scilab определены операции над комплексными числами.

clc

a=input('a=');

b=input('b=');

c=input('c=');

d=b*b-4*a*c;

x1=(-b+sqrt(d))/2/a;

x2=(-b-sqrt(d))/2/a;

disp(x1,x2);

a=-->1

b=-->2

c=-->3

- 1. - 1.4142136i

- 1. + 1.4142136i

Комплексные корни квадратного уравнения