
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ООП и последовательность построения диаграмм
Прочитав материал этой лекции, нетерпеливый читатель скажет: "Это ведь все элементарно!". Да, это правда, простые задачи решаются с помощью UML без особого труда. А вот более сложные системы, прочитав только эту лекцию, возможно, так же адекватно смоделировать не удастся. Естественно, читать об UML недостаточно - надо им пользоваться! Может быть, даже сразу вы чего-то и не поймете, но по мере увеличения опыта использования UML вы все лучше начнете понимать его конструкции. Так же как и другие языки, UML требует особого способа мышления, умения рассматривать систему с разных сторон и точек зрения.
Можно дать множество рекомендаций относительно того, какие же именно диаграммы строить и как, но мы будем краткими. Прежде всего, вы должны ответить для себя на такие вопросы:
· Какие именно виды диаграмм лучше всего отражают архитектуру системы и возможные технические риски, связанные с проектом?
· Какие из диаграмм удобнее всего превратить в инструмент контроля над процессом (и прогрессом) разработки системы?
И еще одно - никогда не выбрасывайте даже "забракованные" диаграммы: они могут в дальнейшем оказаться полезными при анализе направления вашей мысли, поиске ошибок проектирования, да и просто для экспериментов по незначительному изменению системы.
Диаграммы, как уже говорилось выше, можно и нужно строить в некоторой логической последовательности. Но как выработать эту последовательность, если у вас нет опыта моделирования? Как научиться этому? Вот несколько простых приемов, которые помогут вам (или вашей команде) выработать свой стиль проектирования.
В UML-проектировании, как и при создании любых других моделей, важно уметь абстрагироваться от несущественных свойств системы. В этом плане очень полезными могут оказаться коллективные упражнения на выявление и анализ прецедентов. Они помогут отработать навыки выявления четких абстракций.
Неплохой способ начать - моделирование базовых абстракций или поведения одной из уже имеющихся у вас систем.
Стройте модели предметной области задачи в виде диаграммы классов! Это хороший способ понять, как визуализировать множества взаимосвязанных абстракций. Таким же образом стройте модели статической части задач.
Моделируйте динамическую часть задачи с помощью простых диаграмм последовательностей и кооперации. Хорошо начать с модели взаимодействия пользователя с системой - так вы сможете легко выделить наиболее важные прецеденты.
Не забываем, что мы говорим, прежде всего, именно об объектноориентированных системах. Поэтому, подытоживая все сказанное ранее, можно предложить такую последовательность построения диаграмм:
· диаграмма прецедентов,
· диаграмма классов,
· диаграмма объектов,
· диаграмма последовательностей,
· диаграмма кооперации,
· диаграмма состояний,
· диаграмма активности,
· диаграмма развертывания.
Конечно, это не единственная возможная последовательность. Возможно, вам будет удобнее начать с диаграммы классов. А может, вам не нужны диаграммы объектов, а диаграммы последовательностей вы предпочитаете диаграммам кооперации. Это лишь один из путей, постепенно вы выработаете свой персональный стиль проектирования и свою последовательность!
И напоследок еще несколько советов относительно использования UML.
Хорошее и полезное упражнение - строить модели классов и отношений между ними для уже написанного вами кода на С++ или Java.
Применяйте UML для того, чтобы прояснить неявные детали реализации существующей системы или использованные в ней "хитрые механизмы программирования".
Стройте UML-модели, прежде чем начать новый проект. Только когда будете абсолютно удовлетворены полученным результатом, начинайте использовать их как основу для кодирования.
Обратите особое внимание на средства UML для моделирования компонентов, параллельности, распределенности, паттернов проектирования. Большинство из этих вопросов мы рассмотрим далее.
UML содержит некоторые средства расширения. Подумайте, как можно приспособить язык к предметной области вашей задачи. И не слишком увлекайтесь обилием средств UML: если вы в каждой диаграмме будете использовать абсолютно все средства UML, прочесть созданную вами модель смогут лишь самые опытные пользователи.
Кроме прочего, важным моментом здесь является выбор пакета UML-моделирования (CASE-средства), что тоже может повлиять на ваш индивидуальный стиль проектирования. Более подробно мы поговорим об этом в одной из последующих лекций, пока же отметим, что все диаграммы, виденные вами в этой лекции, построены с помощью TAU G2 от Telelogic.
Выводы
· Диаграммы разных видов позволяют взглянуть на систему с разных точек зрения.
· UML содержит диаграммы трех типов - для моделирования статической структуры, поведенческих аспектов и подробностей реализации приложения.
· Недостаточно читать об UML - им надо пользоваться!
Контрольные вопросы
· Почему нужно строить разные диаграммы при моделировании системы?
· Какие диаграммы соответствуют статическому представлению о системе?
· Вы разрабатываете компьютерную программу для игры в шахматы. Какая диаграмма UML была бы полезной в этом случае? Почему?
· Составьте список вопросов потенциальному пользователю такой программы. Объясните, почему вы хотели бы задать именно их.
Национальный Открытый Университет "ИНТУИТ": www.intuit.ru
Александр Бабич
Лекция 4. Диаграмма классов: крупным планом
Как класс изображается на диаграмме UML?
Архитектор программного обеспечения в первую очередь обращает внимание на объекты предметной области. Программист же концентрируется на поведении этих объектов, пользуясь классами, к которым они принадлежат. Вот поэтому-то диаграмма классов и является одной из важнейших диаграмм UML. Она используется для документирования программных систем, и основным ее компонентом является класс. Что такое класс, мы уже говорили ранее, когда знакомились с видами диаграмм UML. В предыдущей лекции мы рассматривали назначение диаграммы классов, знакомились с примерами готовых диаграмм, но не вникали в тонкости обозначений, используемых на диаграмме. В тех примерах все казалось нам очень понятным и логичным. Тем не менее, некоторые нюансы все же следует рассмотреть, и как раз этим мы сейчас и займемся.
Класс на диаграмме изображается в виде прямоугольника, разделенного горизонтальными линиями на три части. В первой части указывается название класса. Как правило, имя класса состоит из одного, максимум двух слов. Вторая часть содержит перечень атрибутов класса, которые характеризуют тот или иной объект этого класса в модели предметной области. Третья часть содержит перечень операций, отражающих его поведение в модели предметной области (рис. 3.1). Все очень просто, не так ли?
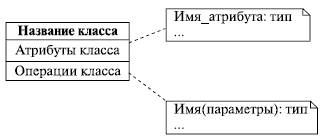
Рис. 3.1.
А что внутри?
Мы узнали, как класс изображается и выглядит "снаружи". А что же внутри объектов класса? Пользователю об этом знать необязательно, более того, абсолютно не нужно. Для человека, использующего его, объект выступает в роли черного ящика. Скрывая от пользователя внутреннее устройство объекта, мы обеспечиваем его надежную работу. Сейчас мы рассмотрим, как убрать из поля зрения пользователя то, что ему знать не нужно.
Читателя может слегка смутить слово "пользователь", которым мы злоупотребляли в предыдущем абзаце. Зачем вообще пользователю какие-то объекты и классы? Внесем ясность. Программист, использующий в своей программе созданные кем-то компоненты, как раз и выступает в роли такого пользователя. Зачем ему знать что внутри - он знает, какие атрибуты надо модифицировать и какие операции использовать, чтобы заставить объект работать именно так, как ему нужно! Более того, а многие ли из нас знают, как именно устроен и по каким принципам работает, например, телевизор - объект класса "Бытовой прибор"?
Сокрытие от пользователя внутреннего устройства объектов называется инкапсуляцией. Если говорить более "научным" языком, то инкапсуляция - это защита отдельных элементов объекта, не затрагивающих существенных характеристик его как целого. Инкапсуляция нужна не только для того, чтобы создать иллюзию простоты объекта для пользователя (по словам Г. Буча). Но вернемся к примеру с телевизором. Нам этот прибор кажется очень простым только потому, что при работе с ним мы используем простой и понятный интерфейс - пульт дистанционного управления. Мы знаем: для того чтобы увеличить громкость звука, надо нажать вот эту кнопку, а чтобы переключить канал - вот эту. Как телевизор устроен внутри, мы не знаем. Более того - в отсутствие пульта ДУ такое знание было бы неудобным для нас и весьма опасным для самого телевизора, вздумай мы увеличить громкость с помощью паяльника. Поэтому-то пульт ДУ и защищает от нас "внутренности" телевизора! Вот так инкапсуляция реализуется в реальном мире.
В программировании инкапсуляция обеспечивается немного по-другому - с помощью т. н. модификаторов видимости. С их помощью можно ограничить доступ к атрибутам и операциям объекта со стороны других объектов. Звучит это немного пугающе, но на самом деле все просто. Если атрибут или операция описаны с модификатором private, то доступ к ним можно получить только из операции, определенной в том же классе. Если же атрибут или операция описаны с модификатором видимости public, то к ним можно получить доступ из любой части программы. Модификатор protected разрешает доступ только из операций этого же класса и классов, создаваемых на его основе. В языках программирования могут встречаться модификаторы видимости, ограничивающие доступ на более высоком уровне, например, к классам или их группам, однако смысл инкапсуляции от этого не изменяется. В UML атрибуты и операции с модификаторами доступа обозначаются специальными символами слева от их имен:
| Символ | Значение |
| + | public - открытый доступ |
| - | private - только из операций того же класса |
| # | protected - только из операций этого же класса и классов, создаваемых на его основе |
Рассмотренный ранее пример с телевизором средствами UML (конечно же, это очень высокоуровневая абстракция) можно изобразить так (рис. 3.2):

Рис. 3.2.
Не правда ли, все понятно и предельно просто? Зачем, например, пользователю знать числовые значения частот каналов? Он знает, что достаточно запустить процедуру автоматического поиска каналов и телевизор все сделает за него. Вот вам и инкапсуляция - оказывается, она повсюду вокруг нас. Оглянитесь и подумайте, сколько вещей вокруг имеют скрытые свойства и выполняют скрытые операции. Испугались? Вот то-то же!
Как использовать объекты класса?
Итак, мы рассмотрели инкапсуляцию - одно из средств защиты объектов. Все вроде бы понятно, но как же именно работать с объектом?
Если уж говорить о защите объекта, то чтобы она действительно была эффективной, надо позаботиться о некоем стандартном и безопасном, не зависящим от языка программирования способе доступа к объекту. К тому же такой стандартный способ доступа должен быть простым и с точки зрения использования, и с точки зрения реализации. Вспомните пример с телевизором. Нажимая кнопки на пульте, мы ожидаем, что телевизор откликнется на это действие каким-то определенным образом - именно так, как мы ожидаем, а не иначе. То есть, с одной стороны, пульт ДУ является средством доступа к скрытым операциям, выполняемым телевизором, а с другой стороны - пульт обеспечивает нужное для нас поведение телевизора. В данном примере именно пульт является таким стандартным средством доступа к телевизору. Можно даже сказать, средством доступа, не зависящим от конкретной модели телевизора - вспомните об универсальных пультах и о том, как отключаете звук надоедливой рекламы на экране в вагоне поезда, используя КПК!
В том же примере с телевизором у нас впервые промелькнуло слово интерфейс. И не случайно промелькнуло: именно так называют тот самый стандартный способ доступа к объекту. Более строго, интерфейс - это логическая группа открытых ( public ) операций объекта. Один и тот же объект может иметь несколько интерфейсов. У телевизора, например, их два - пульт ДУ и кнопки на корпусе. А может и больше - вспомните о возможности управлять бытовой техникой с помощью КПК или универсального пульта ДУ.
Кстати, посмотрите внимательнее на пульт ДУ или на экран программы удаленного контроля. Что вы видите - кнопки? Или кнопки, сгруппированные по функциональному признаку? Да, именно так: кнопки, переключающие каналы, расположены отдельно, рядом - группа кнопок, отвечающих за регулировку громкости звука, рядом - группа программируемых кнопок, и т. д. В принципе, можно сказать, что пульт реализует не один, а несколько интерфейсов - по числу функциональных групп кнопок. Впрочем, это уже формализм: мы просто хотели проиллюстрировать слова "логическая группа" в определении интерфейса.
Однако интерфейс - это не только и не столько группа операций объекта. Интерфейс отражает внешние проявления объекта, показывает, каким образом осуществляется взаимодействие с ним, скрывая остальные детали, не имеющие отношения к процессу взаимодействия.
Интерфейс всегда реализуется некоторым классом, который в таком случае называют классом, поддерживающим интерфейс. Как мы уже говорили ранее, один и тот же объект может иметь несколько интерфейсов. Это означает, что класс этого объекта реализует все операции этих интерфейсов. К данному моменту в голове читателя может созреть вопрос: "Мы же, вроде бы, говорили о классах и объектах, а теперь вдруг перешли на интерфейсы. Да и вообще, используются ли они в практике программирования или являются просто изящной теоретической конструкцией?". Ответ на этот вопрос прост: многие из существующих технологий программирования (например, COM, CORBA, Java Beans) не только активно используют механизм интерфейсов, но и, по сути, полностью основаны на нем.
Что ж, наверное, пришло время поговорить о том, как интерфейс изображается на диаграммах. Изображаться он может несколькими способами. Первый и самый простой из них - это класс со стереотипом <<interface>> (рис. 3.3):

Рис. 3.3.
Этот способ хорош, если нужно показать, какие именно операции предоставляет интерфейс. Если же такие подробности в данный момент не важны, предоставляемый интерфейс изображают в виде кружочка или, как говорят, "леденца" ( lollipop ) (рис. 3.4):

Рис. 3.4.
Обратите внимание на маленький значок на закладке папки ConduitSet. Это обозначение подсистемы, мы могли бы не рисовать его, а просто использовать стереотип <<subsystem>>. Впрочем, об этом мы еще поговорим.
И наконец, еще один способ изображения интерфейса. Он не является альтернативой описанным ранее способам, а используется для изображения интерфейсов, требующихся объекту для выполнения его работы. Обозначается он очень простым и логичным символом. Впрочем, судите сами (рис. 3.5):

Рис. 3.5.
Наблюдательный читатель уже, наверное, заметил, как логически совмещаются символы предоставляемого и требуемого интерфейсов.
Действительно, на диаграммах довольно часто можно увидеть такую картинку (рис. 3.6):
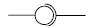
Рис. 3.6.
Да, кстати, вы заметили, что названия интерфейсов начинаются с буквы I? Эта традиция пошла из языка Java, и, как показывает практика, она весьма облегчает жизнь, если нужно, например, быстро разобраться в сложной диаграмме, составленной другим человеком.
Всегда ли нужно создавать новые классы?
Начнем с вопроса, казалось бы, не имеющего никакого отношения к рассматриваемому вопросу, а именно - всегда ли нужно создавать новый класс для каждой новой задачи? Правильный ответ, конечно же, "нет". Это было бы странно и неэффективно. "Фишка" состоит в том, что мы можем использовать уже существующие классы, адаптируя их функциональность для выполнения новых задач. Таким образом появляется возможность не создавать систему классов с нуля, а задействовать уже имеющиеся решения, которые были созданы ранее, при работе над предыдущими проектами. Впрочем, наше высказывание о странности и неэффективности создания новых классов не является истиной в последней инстанции. Могут быть ситуации, когда существующие классы по каким-либо причинам не устраивают архитектора, и тогда требуется создать новый класс. Следует, однако, избегать ситуаций, когда созданный класс (а точнее, его набор операций и атрибутов) практически повторяет существующий, лишь незначительно отличаясь от него. Все-таки лучше не изобретать велосипед и стараться создавать классы на основе уже существующих, и только если подходящих классов не нашлось - создавать свои, которые, в свою очередь, могут (и должны!) служить основой для других классов. Мы уже не говорим о том, что создание классов предполагает значительный объем усилий по кодированию и тестированию. В общем случае, сказанное выше можно проиллюстрировать такой диаграммой (рис. 3.7):

Рис. 3.7.
В дополнение можно назвать несколько причин, почему стоит использовать уже существующие классы:
Во-первых, идя этим путем, мы пользуемся плодами ранее принятых решений. Действительно, если когда-то мы уже решили некоторую проблему, зачем начинать все "с нуля", повторяя уже однажды проделанные действия?
Во-вторых, таким образом мы делаем решение мобильным и расширяемым. Используя уже существующие классы и создавая на их основе новые, мы можем развивать решение практически неограниченно, добавляя лишь необходимые нам в данный момент детали - атрибуты и операции.
В-третьих, существующие классы, как правило, хорошо отлажены и показали себя в работе. Разработчику не надо тратить время на кодирование, отладку, тестирование и т. д., - мы работаем с хорошо отлаженным и проверенным временем кодом, который зарекомендовал себя в других проектах и в котором уже выявлено и исправлено большинство ошибок.
А теперь внимание - мы много говорили о том, что нужно создавать классы на основе уже существующих, но так и не сказали ни слова о том, как это сделать. Пришло время внести ясность в этот вопрос. Тем самым мы подбираемся к понятию обобщения или генерализации, которое играет очень важную роль в ООП, являясь одним из его базовых принципов. Обобщение- это отношение между более общей сущностью, называемой суперклассом, и ее конкретным воплощением, называемым подклассом. Иногда обобщение называют отношениями типа "является", имея в виду, что одни сущности (например, круг, квадрат, треугольник) являются воплощением более общей сущности (например, класса "геометрическая фигура"). При этом все атрибуты и операции суперкласса независимо от модификаторов видимости входят в состав подкласса.
Обобщение (или, как часто говорят, наследование) на диаграммах обозначается очень просто - незакрашенной треугольной стрелкой, направленной на суперкласс (рис. 3.8).
Для того чтобы научиться эффективно моделировать наследование, обратимся к классикам, а именно к Г. Бучу. Он советует проводить эту процедуру в такой последовательности:
1. Найдите атрибуты, операции и обязанности, общие для двух или более классов из данной совокупности. Это позволит избежать ненужного дублирования структуры и функциональности объектов.
2. Вынесите эти элементы в некоторый общий суперкласс, а если такого не существует, то создайте новый класс.
3. Отметьте в модели, что подклассы наследуются от суперкласса, установив между ними отношение обобщения.
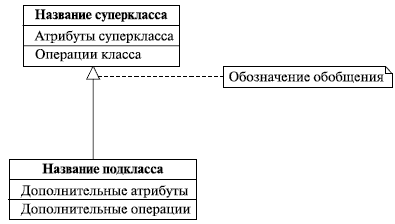
Рис. 3.8.
А вот и пример применения этого подхода (рис. 3.9):

Рис. 3.9.
На первый взгляд, кажется странным, что класс "точка" не имеет никаких атрибутов, а круг имеет только радиус. С прямоугольником, вроде бы, все понятно - ширина и высота, но вот только где он расположен в пространстве, этот прямоугольник? Давайте попробуем следовать советам Буча. Итак, положение всех трех фигур можно однозначно определить с помощью пары чисел. Для точки - это вообще единственные ее характеристики, для круга и прямоугольника - их центры (под центром прямоугольника мы понимаем точку пересечения его диагоналей). Вот они, общие атрибуты! Таким образом, мы создали суперкласс "Фигура", имеющий два атрибута - координаты центра. Все остальные классы на этой диаграмме связаны с классом "Фигура" отношением обобщения, т. е. в них нужно доопределить только "недостающие" атрибуты - радиус, ширину и высоту. Атрибуты, описывающие координаты центра, эти классы имеют изначально как потомки класса "Фигура" - они их наследуют. Заметим, что операции классов мы тут не рассматриваем: понятно, что с ними была бы та же история.
Так, с наследованием вроде бы разобрались. Пришло время для маленькой провокации с нашей стороны. Классы-потомки ведь наследуют атрибуты и операции суперкласса? Таким образом, они могут наследовать и их интерфейсы - то есть объекты абсолютно разной природы могут иметь один и тот же интерфейс! Так как же тогда определить, какого же все-таки класса объект? Да и нужно ли это вообще?
Действительно, объекты разной природы (или говоря проще, разных классов) могут поддерживать один и тот же интерфейс именно так, как того ожидает пользователь. Примером тому может служить рассмотренная выше диаграмма с геометрическими фигурами. Все рассмотренные фигуры имеют, например, операцию рисования на экране. С точки зрения пользователя в каждом случае это одно и то же действие. Однако реализованы эти операции по-разному - ведь процедура изображения прямоугольника сильно отличается от подобной процедуры для круга. Но для пользователя это неважно: ведь сигнатура-то одна и та же! А возможно это благодаря еще одному из основных принципов ООП - полиморфизму. Как мы только что упомянули, работа механизма полиморфизма основана на совпадении сигнатуры метода, объявленного в интерфейсе, и сигнатуры самого метода. Методы внутри классов-потомков могут быть (и наверняка будут!) переопределены, их реализации будут различными, а сигнатуры останутся неизменными. Таким образом (и в этом легко ощутить мощь ООП), выполняя одни и те же операции, разные объекты могут вести себя по-разному.
Полиморфизм является основой для реализации механизма интерфейсов в языках программирования. Вот, кстати, и ответ на вопрос, какого класса объект: как только пользователь обращается к некоторой операции через интерфейс, определяется фактический класс объекта и вызывается соответствующая операция класса. Примеры полиморфизма можно увидеть в самых обыденных вещах, которыми мы пользуемся в повседневной жизни. Оглянитесь вокруг - мир построен по ООП, Матрица работает! Например, всем привычная кредитная карточка, является интерфейсом для доступа к банковскому счету через банкомат (и не только), одинаково работает в любой стране, вот только ведет себя чуть-чуть по-разному, т. к. банкомат выдает деньги в местной валюте. Согласны, пример не очень корректный, но зато очень наглядный! Думаем, понаблюдав за окружающим миром, читатель сам сможет привести массу примеров полиморфизма.
Инкапсуляция, наследование и полиморфизм, с которыми мы только что познакомились, являются теми самыми тремя китами, на которых держится ООП. Если вы поняли суть этих базовых принципов и осознали их истинную мощь, вы прошли большую часть пути, ведущего к полному овладению ООП как наиболее адекватной методикой описания (так и тянет сказать "проектирования") окружающего нас мира.
Отношения между классами
Ни один из объектов окружающего нас мира не существует сам по себе. Птицы летают потому, что есть воздух, на который опираются их крылья. Каждый из нас связан с массой других людей разнообразными родственными, профессиональными и другими связями, предполагающими различные типы отношений. Точно так же и классы связаны между собой. И чтобы в полной мере овладеть ООП, нам необходимо понять суть этих отношений и научиться их идентифицировать.
Мы сказали, что объекты находятся в определенных отношениях друг с другом. Один из типов таких отношений - это зависимость. Думаем, суть такого отношения понятна уже из его названия - зависимость возникает тогда, когда реализация класса одного объекта зависит от спецификации операций класса другого объекта. И если изменится спецификация операций этого класса, нам неминуемо придется вносить изменения и в зависимый класс. Приведем простой пример, опять-таки взятый из нашей повседневности. Иногда к нам в руки попадают видеофайлы, воспроизвести которые "с лету" не удается. Почему? Правильно, потому что на компьютере не установлены соответствующие кодеки. То есть операция "Воспроизведение", реализуемая программой-медиаплеером, зависит от операции "Декомпрессия", реализуемой кодеком. Если спецификация операции "Декомпрессия" изменится, придется менять код медиаплеера, иначе он просто не сможет работать с каким-то кодеком и, в лучшем случае, завершит свою работу с ошибкой. А вот так зависимость между классами изображается в UML (рис. 3.10):

Рис. 3.10.
Стоит отметить, что зависимости на диаграммах изображают далеко не всегда, а только в тех случаях, когда их отображение является важным для понимания модели. Часто зависимости лишь подразумеваются, т. к. логически следуют из природы классов.
Другой вид отношений между объектами - это ассоциация. Это просто связь между объектами, по которой можно между ними перемещаться. Ассоциация может иметь имя, показывающее природу отношений между объектами, при этом в имени может указываться направление чтения связи при помощи треугольного маркера. Однонаправленная ассоциация может изображаться стрелкой. Проиллюстрируем сказанное примерами (рис. 3.11):

Рис. 3.11.
Кроме направления ассоциации, мы можем указать на диаграмме роли, которые каждый класс играет в данном отношении, и кратность, то есть количество объектов, связанных отношением (рис. 3.12):

Рис. 3.12.
И насчет ролей, и насчет кратности на этой диаграмме все понятно - человек может вообще не работать, работать в одной или более компаниях, а вот компании в любом случае нужен хотя бы один сотрудник. Кстати, о кратности. Ассоциация может объединять три и более класса. В этом случае она называется n-арной и изображается ромбом на пересечении линий, как показано на этой диаграмме, позаимствованной нами из Zicom Mentor (рис. 3.13):
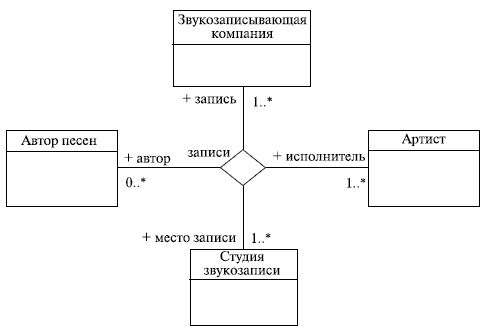
Рис. 3.13.
Ранее мы говорили, что ассоциация - это "просто связь" между объектами. На самом деле, в реальности связи бывают "просто связями" крайне редко. Обычно при ближайшем рассмотрении под ассоциацией понимается более сложное отношение между классами, например, связь типа "часть-целое". Такой вид ассоциации называется ассоциацией с агрегированием. В этом случае один класс имеет более высокий статус (целое) и состоит из низших по статусу классов (частей). При этом выделяют простое и композитное агрегирование и говорят о собственно агрегациии композиции. Простая агрегация предполагает, что части, отделенные от целого, могут продолжать свое существование независимо от него. Под композитным же агрегированием понимается ситуация, когда целое владеет своими частями и их время жизни соответствует времени жизни целого, т. е. независимо от целого части существовать не могут. Примеры этих видов ассоциаций и их обозначений в UML можно увидеть на следующей диаграмме (рис. 3.14).

Рис. 3.14.
Примеры, как нам кажется, очень простые и понятные. Винчестер можно вынуть из компьютера и установить в новый компьютер или в USB-карман, т. е. существование жесткого диска с разборкой системного блока не заканчивается. А вот кнопки без окон обычно существовать не могут - с закрытием окна кнопки также исчезают.
И, наконец, еще одна важная вещь, касающаяся ассоциации. В отношении между двумя классами сама ассоциация тоже может иметь свойства и, следовательно, тоже может быть представлена в виде класса. Пример прост (рис. 3.15):

Рис. 3.15.
Действительно, перед началом трудовых отношений работник и работодатель подписывают между собой контракт, который имеет такие атрибуты, как, например, описание работ, сроки их выполнения, порядок оплаты и т. д.
А вот более сложный, но, опять-таки, взятый из реальной жизни пример моделирования отношений между классами, позаимствованный нами из Zicom Mentor (рис. 3.16):

Рис. 3.16.
И наконец, доказательство того, что UML можно использовать для чего угодно, в том числе и для записи сказок: диаграмма, описывающая предметную область сказки о Курочке Рябе и взятая с сайта конкурса шуток на UML (http://www.umljokes.com/) (рис. 3.17):
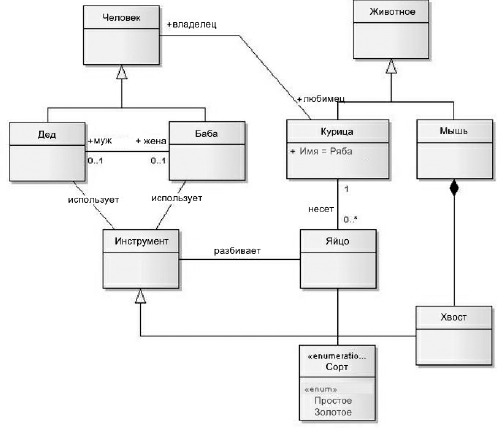
Рис. 3.17.
Узнаете рассказ, знакомый с детства?
Выводы
· Инкапсуляция защищает внутреннее устройство объекта и реализуется путем ограничения доступа к атрибутам и операциям класса из других частей программы.
· Обобщение позволяет повторно использовать уже существующие решения, создавая новые классы путем наследования от имеющихся классов.
· Полиморфизм позволяет работать с группой разнородных объектов одинаковым образом, не задумываясь о различиях в реализации.
· Инкапсуляция, наследование и полиморфизм - три кита, на которых держится ООП.
· В любой системе между объектами существуют отношения разных типов.
· Отношение зависимости означает, что реализация одного класса зависит от спецификации операций другого класса.
· Ассоциация выражает отношение между несколькими равноправными объектами и может иметь направление, роли и кратность, а также изображаться в виде класса ассоциации.
· Композиция и агрегация используются, если между объектами существуют отношения типа "часть-целое", причем композиция предполагает, что части не могут существовать отдельно от целого.
Контрольные вопросы
· Какие три принципа лежат в основе ООП?
· Что такое интерфейс? На каком из базовых принципов ООП основан механизм интерфейсов?
· Что такое n-арная ассоциация?
· В чем разница между агрегацией и композицией?
· Что такое класс ассоциации?
Лекция 5. Диаграмма активностей: крупным планом
А ведь это вовсе не блок-схема!
Как мы уже говорили, диаграммы активностей (Activity Diagrams) являются представлением алгоритмов неких действий (активностей), выполняющихся в системе. Мы уже знаем, что нотация UML предлагает пять представлений системы:
· Вид системы с точки зрения прецедентов.
· Вид с точки зрения проектирования.
· Вид с точки зрения процессов.
· Вид с точки зрения развертывания.
· Вид с точки зрения реализации.
И при этом каждый из перечисленных способов представления системы может содержать последовательности действий, которые могут быть описаны с помощью алгоритмов. Вот здесь-то и выходят на сцену диаграммы деятельностей. Вообще говоря, любой элемент модели, имеющий динамическое поведение, может быть дополнен диаграммой деятельности - именно для уточнения этой самой динамики. Как хорошо подходящий по контексту пример следует упомянуть возможность применения диаграмм активности для описания бизнес-процессов, существующих в компании (нотации Grapes-BM, BPML/BPMN и др.). Вот уж где самая что ни на есть динамика!
Можно построить несколько диаграмм деятельности для одной и той же системы, причем каждая из них будет фокусироваться на разных аспектах системы, показывать различные действия, выполняющиеся внутри ее. Читатель, конечно же, понял, что, когда мы говорим о динамике, мы подразумеваем поведение системы в целом или ее частей. Говоря более формально, диаграммы активности, в общем-то, не имеют монополии на описание поведенческих особенностей динамических частей системы. Для этой же цели могут использоваться еще диаграммы прецедентов, последовательности, кооперации и состояний. Почему же мы говорим именно о диаграмме активности? Нет, не только потому, что так называется эта лекция.
Именно на диаграмме деятельности представлены переходы потока управления от одной деятельности к другой. Это, по сути, разновидность диаграммы состояний, где все или большая часть состояний являются некоторыми деятельностями, а все или большая часть переходов срабатывают при завершении определенной деятельности и позволяют перейти к выполнению следующей. Как мы уже говорили (повторение - мать учения), диаграмма деятельности может быть присоединена к любому элементу модели, имеющему динамическое поведение. Кстати, исходя из вышесказанного, логичнее говорить не "диаграмма деятельности", а "диаграмма деятельностей" - во множественном числе. А еще мы предполагаем, что читатель понимает смысл понятий "деятельность", "переход" и "объект". Об объектах как об экземплярах классов мы уже говорили ранее. Понятия же деятельности (activity) как протяженного во времени составного (неатомарного) вычисления (действия, action) и перехода как передачи контроля, надеемся, понятны интуитивно, без дополнительных объяснений.
Диаграммы деятельности позволяют моделировать сложный жизненный цикл объекта, с переходами из одного состояния (деятельности) в другое. Но этот вид диаграмм может быть использован и для описания динамики совокупности объектов. Они применимы и для детализации некоторой конкретной операции, причем, как мы увидим далее, предоставляют для этого больше возможностей, чем "классическая" блок-схема. Диаграммы деятельности описывают переход от одной деятельности к другой, в отличие от диаграмм взаимодействия, где акцент делается на переходах потока управления от объекта к объекту.
Как говорится, лучше один раз увидеть, чем сто раз услышать. Мы достаточно разрекламировали диаграммы деятельностей. Пора взглянуть на пример (рис. 4.1).

Рис. 4.1.
Эта диаграмма довольно точно описывает ежеутреннюю последовательность действий автора этих строк (до момента ухода на работу). Как видим, все очень просто и понятно. Действия показаны скругленными прямоугольниками, как в блок-схеме, - мы узнаем даже ромбик символа принятия решения с обозначениями условий возле переходов. Да, отличия от блок-схемы не так уж сильны. Более того, эти отличия выглядят как логичное расширение нотации блок-схем. Обратим внимание на то, что начало и конец уже не изображаются одинаковым безликим кружком. Начало теперь закрашено, а конец изображен в виде символа, напоминающего кошачий глаз (рис. 4.2) (кстати, это образное название - "кошачий глаз" - уже намертво въелось в жаргон архитекторов и аналитиков).
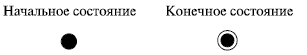
Рис. 4.2.
Без пояснений понятен также смысл символа, предшествующего принятию душа и пению и следующего за ними - он означает распараллеливание, а затем опять слияние воедино ( синхронизацию ) потоков управления, т. е. операции "пение" и "душ" выполняются одновременно. Нотация проста: несколько потоков управления сливаются в один или один поток разделяется на несколько. Третьего не дано (рис. 4.3).

Рис. 4.3.
Конечно, это не единственные отличия диаграммы активностей от блок-схемы. На диаграмме деятельностей можно не только показать параллельно выполняемые действия, но и указать состояния объектов (так же, как и на представлениях конечных автоматов, о которых нам так много говорили в университетах), также есть возможность показывать распределение ролей и т. д. Вот еще пример, подтверждающий, что диаграмма активностей - это нечто большее, чем блок-схема (рис. 4.4).
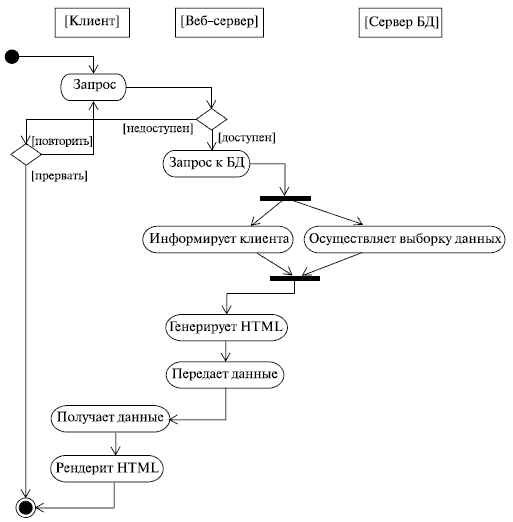
Рис. 4.4.
Смысл диаграммы вполне понятен и без дополнительных объяснений. Как вы уже, конечно, догадались, на ней показана работа с веб-приложением, которое решает некую задачу в удаленной базе данных. Привлекает внимание странное расположение активностей на этой диаграмме: они как бы разбросаны по трем беговым дорожкам, каждая из которых соответствует поведению одного из трех объектов - клиента, веб-сервера и сервера баз данных. Благодаря этому легко определить, каким из объектов выполняется каждая из активностей, и неожиданно приходит понимание того, что "странность" этой диаграммы, оказывается, очень упрощает ее восприятие.
Аналогия с дорожками действительно очень удачна. Именно таково официальное название элемента нотации UML, позволяющего указать распределение ролей на диаграмме активностей. Только дорожки это не беговые, а плавательные - они так и называются: swimlanes. Более формально, дорожка - часть области диаграммы деятельности, на которой отображаются только те деятельности, за которые отвечает конкретный объект.

Рис. 4.5.
Предназначены они для разбиения диаграммы в соответствии с распределением ответственности за действия. Имя дорожки может означать роль или объект, которому она соответствует. При использовании дорожек нотация слегка изменяется. Вот как, к примеру, выглядит диаграмма из предыдущего примера, перерисованная с использованием дорожек (рис. 4.5).
Кстати, дорожки могут быть не только вертикальными, но и, если вам как автору так удобнее, горизонтальными. Изображаются горизонтальные дорожки аналогично - просто поверните "обычные" дорожки на 90 градусов против часовой стрелки!
Есть еще один нюанс нотации диаграмм активностей, о котором мы пока не говорили: это так называемая траектория объекта, или поток объекта ( object flow ). Суть его состоит в том, что на диаграмме деятельности можно изобразить и объекты, относящиеся к деятельности. С помощью символа зависимости (пунктирная стрелка, помните?) эти объекты можно соотнести с той деятельностью или переходом, где они создаются, изменяются или уничтожаются. Представим такую ситуацию из повседневной жизни: вы приходите в какой-нибудь фастфуд и заказываете гамбургер с колой. Что, знакомо? Во время приготовления завтрака повар создает новый объект - гамбургер. Пока вы нетерпеливо выпиваете колу, официант перемещает этот объект (подает ваш заказ). Естественно, во время завтрака вы уничтожаете этот объект. Вот как это выглядит на диаграмме (рис. 4.6).
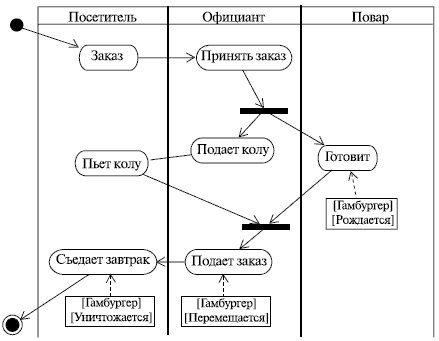
Рис. 4.6.
На этом можно было бы и закончить наш разговор о нотации диаграмм активностей и их отличиях от блок-схем. Если бы не одно НО. Мы говорили, что деятельность - это протяженное по времени составное действие. Составное! То есть составленное из более простых действий. Вот эти-то самые простые (атомарные) действия, а вернее, последовательность их выполнения, частенько изображают внутри деятельности в виде маленькой диаграммы активностей. Это слегка напоминает матрешку - одна (а часто и не одна) диаграмма внутри другой. Мы не будем долго говорить об этом: нашей целью было просто обратить внимание читателя на подобную возможность "вложенных" диаграмм. Мы просто покажем пример, позаимствованный нами из Zicom Mentor (рис. 4.7).

Рис. 4.7.
Диаграмма описывает высадку пассажиров самолета, достигших пункта назначения, и посадку новых пассажиров. Предлагаем читателю самому внимательно рассмотреть эту диаграмму. Из нее, например, можно почерпнуть, что конечных состояний может быть больше одного. Кстати, кроме начального и конечного состояний есть еще конечное состояние потока (Flow final mode). От конечного состояния оно отличается вот чем: конечное состояние потока означает завершение одного потока управления, а конечное состояние говорит о завершении всех потоков управления внутри деятельности. Обозначается конечное состояние потока простым символом, напоминающим лампочку накаливания в схемах электрических цепей (рис. 4.8):

Рис. 4.8.
Право найти примеры использования конечного состояния потока (уверяем вас, оно используется не так уж и часто), мы предоставляем читателю.
Примеры использования таких диаграмм
На практике диаграммы деятельности применяются в основном двумя способами:
1. Для моделирования процессов
В этом случае внимание фокусируется на деятельности с точки зрения экторов, которые работают с системой. Внимательный читатель, конечно же, вспомнит, что чуть ранее мы уже говорили о применимости диаграмм деятельности для описания бизнес-процессов. В случае такого использования диаграмм деятельности активно используются траектории объектов. Действительно, вспомним наш пример с гамбургером: изменив роли и деятельности, легко представить на его месте некий документ. Ведь правда?
2. Для моделирования операций
В этом случае диаграммы деятельности играют роль "продвинутых" блок-схем и применяются для подробного моделирования вычислений. На первое место при таком использовании выходят конструкции принятия решения, а также разделения и слияния потоков управления ( синхронизации ).
Рассмотрим подробнее первый случай. Все мы, конечно, понимаем бизнес-процесс как последовательность неких действий, ведущую к достижению определенных бизнес-целей. Когда мы произносим это слово, в голове рождается множество ассоциаций, как то: люди, занимающие конкретные должности в управленческом аппарате (экторы), документы, которые они создают (артефакты, объекты), процесс принятия решений и передачи приказов по организационной цепочке (управляющие сигналы). Причем обычно все эти сущности связаны друг с другом просто невообразимым количеством явных и неявных связей, так что охватить взглядом целостную картину всего происходящего на предприятии обычно не так просто. А как же тогда все это моделируют?
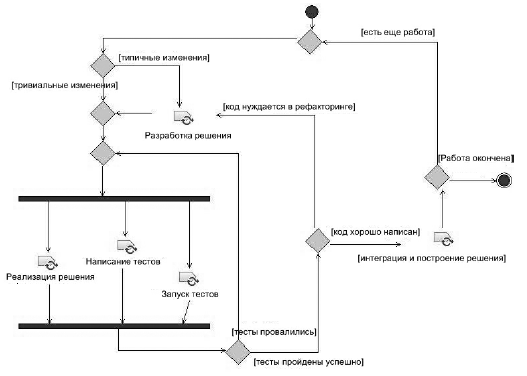
Моделируют бизнес-процессы в несколько этапов, первым из которых является разбиение их на подпроцессы. Подпроцессы, являющиеся "участками большого процесса", описать легче. А там, глядишь, и составится целое из частей. Дальше выделяют ключевые объекты (и создают для них дорожки), определяют предусловия и постусловия каждого процесса (т. е. его границы), описывают деятельности и переходы, отображают на диаграммах состояния ключевых объектов, в которые они переходят в ходе процесса. Все это звучит довольно сложно, а на практике происходит еще сложнее: ведь создается не какая-то абстрактная диаграмма, а модель реального бизнес-процесса в реальной компании, занимающейся реальным бизнесом, где цена ошибки может быть очень высока. Чтобы окончательно не запугать читателя, приведем просто пример использования диаграммы активностей для описания процесса разработки ПО в OpenUP (рис. 4.9):
увеличить изображение
Рис. 4.9.
Выглядит, конечно, не совсем так, как мы привыкли, но все же, сомнений не остается - да, это именно диаграмма активностей. Нотация слегка отличается, но все понятно и без дополнительных пояснений.
А теперь перейдем к рассмотрению моделирования операций с помощью диаграмм активностей. Как мы уже говорили, в этом случае диаграмма активностей превращается в "продвинутую" блок-схему, предоставляющую дополнительные возможности, например, отображение параллельно выполняющихся операций. Возникает соблазн попытаться выполнить кодогенерацию такой диаграммы или даже откомпилировать ее и сразу получить выполняемый файл. Поспешим отметить, что вы не одиноки в таком желании - попыток создать пакет для генерации приложений непосредственно из диаграмм UML было предпринято множество. Некоторые даже оказались более-менее удачными - вспомним, например, Rational Rose Real Time. Таким образом, при моделировании операций UML становится языком визуального программирования!
Приведем пример моделирования одной из базовых алгоритмических конструкций, например, цикла с постусловием (рис. 4.10):

Рис. 4.10.
Ну что, почувствовали себя опять студентом?
Советы по построению диаграмм активностей
Процесс построения диаграммы активностей можно описать в виде последовательности таких действий:
1. Составление перечня деятельностей в системе
Как исходные данные для этой операции хорошо подходит список прецедентов (или список операций - см. два способа использования диаграмм деятельности). Дополняться диаграммой активности может каждый сценарий использования. Можно также попытаться описать связь между ними.
2. Принятие решения о необходимости построения диаграммы деятельностей
Несмотря на то что вы уже начали работу в этом направлении, вы все же можете решить отказаться от продолжения построения диаграммы деятельностей. Причины тому могут быть различными, например, система одномоментно меняет свои состояния (как светофор) или ее поведение достаточно очевидно. (Помните пример с циклом с постусловием? Наверняка многие читатели подумали: "Зачем моделировать такие простые и очевидные вещи?". Теперь вы знаете зачем - чтобы показать нецелесообразность этого.)
3. Определение зависимостей между деятельностями
Для каждой активности нужно найти активности, непосредственно предшествующие (и следующие за ней тоже), то есть активности, без выполнения которых поток управления не может перейти к данной деятельности.
4. Выделение параллельных потоков деятельностей
Выделите активности, имеющие общих предшественников. Зачем - думаем, и так понятно.
5. Определение условий переходов
Сформулируйте выражения, которые могут принимать только два значения - "истинно" или "ложно", соответствующие альтернативным потокам управления. Теперь вы знаете, что писать рядом с символами принятия решений!
6. Уточните сложные деятельности
Повторите пункты 1-6 для каждой из деятельностей (при необходимости). Помните пример с посадкой/высадкой пассажиров самолета? Присмотритесь внимательно, возможно, в проектируемой вами диаграмме тоже будет нелишним применить "принцип матрешки". А как это работает на практике? Да легко! Рассмотрим, например, моделирование пословицы "После драки кулаками не машут":
1. Выделяем деятельности: драться, махать кулаками.
2. Следует ли строить диаграмму в этом случае? Вообще-то нет. Но ведь это пример!
3. Определяем зависимости между деятельностями: размахивание кулаками не происходит после драки.
4. Определяем параллельные деятельности: вроде бы тут таких не наблюдается...
5. Определяем условия переходов: драка состоялась? Если "нет", то машем кулаками, если "да", то нет.
6. Уточняем сложные деятельности: при драке машут не только кулаками, но и ногами. А еще можно пинаться головой и использовать подручные средства, мебель, например. Плюс можно выделить еще подготовительные деятельности (выбор места для нападения) и завершающие (вынос раненых).
Посмеялись? А теперь попробуйте все это смоделировать. Правда, легко? Ведь все уже разложено по полочкам - только рисуй! А что относительно процесса построения диаграмм активностей говорят классики? Тот же Буч, например, писал:
Создавая диаграммы деятельности, не забывайте, что они лишь моделируют срез некоторых динамических аспектов поведения системы. С помощью единственной диаграммы деятельности никогда не удастся охватить все динамические аспекты системы. Вместо этого следует использовать разные диаграммы деятельности для моделирования динамики рабочих процессов или отдельных операций.
Что ж, напутствия сделаны, цитата классика приведена. На этом можно и заканчивать. И все же хотелось бы еще раз напомнить о том, что UML в целом и диаграммы активностей в частности обладают немалыми выразительными средствами, позволяющими не только моделировать сложные бизнес-системы, но и рассказывать сказки, стихи, шутить. Да, вы догадались правильно: мы хотим привести еще пару примеров с сайта шуток на UML (http://www.umljokes.com). Первый пример - это незабвенный шекспировский монолог Гамлета на UML (рис. 4.11).

Рис. 4.11.
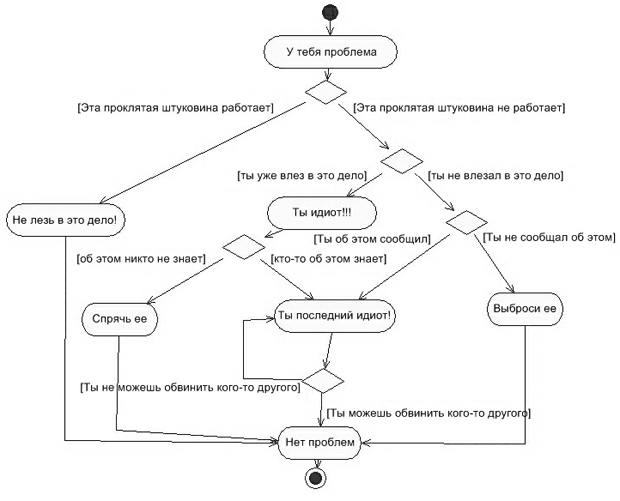
Второй пример - это подход к решению разнообразнейших проблем, знакомый многим из нас. Как видим, в мире он широко известен и пользуется популярностью не только в постсоветских странах (рис. 4.12).
увеличить изображение
Рис. 4.12.
Выводы
· Диаграммой деятельности можно дополнить любой элемент модели, имеющий динамическое поведение.
· Диаграммы деятельности являются частным случаем диаграммы состояний.
· В отличие от блок-схем, диаграммы деятельности могут отображать одновременно выполняемые действия.
· На диаграммах активности можно использовать плавательные дорожки, распределяющие деятельности в соответствии с ролями (объектами), их выполняющими.
· Траектория объекта позволяет показать объекты, относящиеся к деятельности, и моменты переходов этих объектов из одного состояния в другое.
· Сложные деятельности можно дополнительно детализировать, разбив на действия и изобразив "диаграмму в диаграмме".
· Диаграммы деятельностей можно использовать для проектирования процессов (например, бизнес-процессов) или операций (вычислений). Во втором случае UML выступает в роли визуального языка программирования.
Контрольные вопросы
· Какие еще виды диаграмм (кроме диаграмм активностей) можно использовать для моделирования динамики системы?
· Чем диаграммы деятельности отличаются от блок-схем? Какие преимущества это сулит разработчикам?
· Что такое траектория объекта?
· Чем конечное состояние потока отличается от конечного состояния деятельности?
· Чем моделирование процессов отличается от моделирования операций?
· Применимы ли диаграммы деятельности безотносительно к ООП?
Лекция 6. Диаграммы взаимодействия: крупным планом
Рекомендации по построению диаграмм взаимодействия. Диаграммы взаимодействия и их место среди других диаграмм UML. Смысл диаграмм взаимодействия интуитивно нам, конечно же, понятен. Однако посмотрим, что о таких диаграммах говорили классики, например Буч. А вот что:
Диаграмма взаимодействия- это диаграмма, на которой представлено взаимодействие, состоящее из множества объектов и отношений между ними, включая и сообщения, которыми они обмениваются. Этот термин применяется к видам диаграмм с акцентом на взаимодействии объектов (диаграммах кооперации, последовательности и деятельности).
Несмотря на то величайшее уважение, которое мы питаем к Г. Бучу, это определение не кажется нам уж очень удачным. Хотя суть понятия оно передает. Наиболее важное слово в этом определении - это слово "сообщения". Действительно, как люди программирующие, мы понимаем, что взаимодействие-то как раз и состоит в обмене сообщениями между объектами! И к вопросу о сообщениях мы в этой лекции еще не раз вернемся. А пока же посмотрим, что Буч говорит дальше.
А дальше он объясняет, что такое диаграммы кооперации и последовательностей.
Диаграмма последовательностей- диаграмма взаимодействия, в которой основной акцент сделан на упорядочении сообщений во времени.
Диаграмма кооперации- диаграмма взаимодействий, в которой основной акцент сделан на структурной организации объектов, посылающих и получающих сообщения.
То есть диаграмма последовательности описывает (и именно поэтому так и называется) последовательность, в которой объекты отправляют и получают сообщения, а диаграмма кооперации - это аналог диаграммы последовательностей, который тоже показывает обмен сообщениями между объектами, но акцентирует внимание на ролях, которые объекты играют во взаимодействии. Эти два типа диаграмм вообще-то взаимозаменяемы, и решение, какую именно из них использовать в каждом конкретном случае, каждый проектировщик принимает исходя из личных предпочтений. Например, автор этих строк считает диаграммы последовательностей более понятным и более выразительным способом моделирования взаимодействий. Ваше мнение может быть противоположным.
А какое же место диаграммы взаимодействия занимают среди других диаграмм UML? На этот вопрос можно ответить двояко. Можно просто говорить о построении диаграмм взаимодействия как об определенном этапе в процессе моделирования. А можно вспомнить о фазах жизненного цикла разработки ПО и посмотреть, где же диаграммы взаимодействия окажутся в таком случае. Да, кстати, кто помнит, какая диаграмма UML наилучшим образом подходит для описания процессов? Хм, что-то не видно леса рук... Ах да, видим одну руку - девушка, сидящая в дальнем углу зала, за колонной... Правильно! Диаграмма активностей. Что ж, попробуем нарисовать диаграмму активностей, описывающую процесс построения модели системы. Вот вариант такой диаграммы, предложенный одним из наших студентов (рис. 5.1):

Рис. 5.1.
М-да, не совсем диаграмма и не совсем активностей. Но все же она показывает то, что мы хотели показать, а именно, что диаграммы взаимодействия строятся после того, как описана структура системы (диаграмма классов, диаграмма компонентов), способы ее взаимодействия с внешним миром (диаграмма прецедентов) и алгоритмы действий, выполняющихся в системе (диаграмме активностей). Это как бы последний штрих, уточнение того, как именно ведет себя система путем изображения взаимодействия объектов внутри ее.
Для того же, чтобы показать место диаграмм взаимодействия в жизненном цикле разработки ПО, нарисуем еще одну "псевдодиаграмму". Правильнее было бы сказать, что та диаграмма, которую вы сейчас увидите (рис. 5.2), показывает, какие артефакты разработки документируются какими диаграммами.

Рис. 5.2.
И опять все вроде бы логично - мы строим диаграммы взаимодействия во время анализа поведения системы. Кстати, из рисунка (сказать "диаграмма" язык не поворачивается) очень хорошо видно, что диаграмма последовательностей и диаграмма кооперации взаимозаменяемы и являются альтернативными друг другу шагами процесса.
Диаграммы последовательностей и их нотация
Вступительная часть этой лекции наконец-то закончилась, и мы с полным правом можем перейти к рассмотрению нотации диаграмм взаимодействия. Начнем с диаграмм последовательностей. Итак, мы уже говорили, что диаграмма последовательностей показывает последовательность, в которой объекты в процессе взаимодействия обмениваются сообщениями. Но как же сами объекты изображаются на такой диаграмме? А изображаются они точно таким же способом, каким мы пользовались ранее. Т. е. объект - это просто прямоугольник, внутри которого указаны подчеркнутые имя объекта и название класса (не обязательно), разделенные двоеточием. Объекты располагаются в верхней части диаграммы друг за другом. А вниз от каждого объекта тянется пунктирная линия, которую называют линией жизни объекта. Линия жизни объекта - это линия, которая изображает существование объекта на протяжении некоторого промежутка времени, и чем длиннее линия, тем дольше существует объект. Сообщения, которыми обмениваются объекты, изображаются в виде стрелок, направленных от линии жизни одного объекта к линии жизни другого. Линии жизни объектов, тянущиеся вниз, играют роль шкалы времени, так что сообщения, отправленные ранее, расположены выше, чем отправленные позже. Таким образом, последовательность сообщений легко читается "сверху вниз". Чуть позже мы еще вернемся к обсуждению сообщений и поговорим о том, каких видов они бывают и как их различить на диаграмме последовательностей. А пока же убедимся, что мы одинаково понимаем сам термин "сообщение": мы рассматриваем сообщение как спецификацию передачи информации от одного объекта к другому. Объект отправляет сообщение в расчете на то, что оно вызовет некую реакцию и за этим последует некоторая деятельность.
Еще одна вещь, которую можно увидеть на диаграммах последовательностей - это длинные прерывистые полосы на линиях жизни. Таким образом обозначаются периоды времени, когда объект имеет фокус управления, т. е. выполняет некоторое действие (причем неважно как - непосредственно или путем вызова некоей подчиненной операции). Фокус управления на диаграммах последовательностей часто не изображают: ведь и так понятно, где он должен располагаться, достаточно взглянуть на положение стрелок, изображающих сообщения. Рисовать фокус или нет - дело привычки каждого проектировщика. Впрочем, многие средства UML- моделирования рисуют фокус автоматически, так что человеку не нужно заботиться о его изображении. Если объект в процессе взаимодействия разрушается, этот факт помечают на его линии жизни крестиком, который, собственно, эту линию и заканчивает. Да, все мы смертны. Иногда так и тянется рука написать "R.I.P." рядом с таким крестиком...
Не полагаясь на выразительную силу и образность наших описаний, все же покажем примеры всех этих обозначений (рис. 5.3).

Рис. 5.3.
А вот еще парочка обозначений. Первое из них - это анонимный эктор, которого изображают, если нужно показать использование объектов системы некоей внешней сущностью или абстрактным пользователем. Второе - это рефлексивное сообщение. Помните, что такое рефлексия? Правильно, самосозерцание! Тут, в принципе, происходит нечто подобное: объект посылает сообщение самому себе. Так рисуют, если нужно показать действие, выполняемое самим объектом (или внутри него), либо то, что объект сам себя вводит в некоторое состояние (рис. 5.4).

Рис. 5.4.
И еще одно - мы легко можем представить ситуацию посылки сообщения в зависимости от истинности некоторого условия. Например, если цена приглянувшейся нам в магазине вещи меньше ста условных единиц, мы вполне можем приобрести ее за наличные. Покупку на сумму от 100 до 1000 долларов можно оплатить кредитной картой, а чтобы купить нечто, стоящее дороже 1000 у. е., придется брать кредит. А как изобразить такие ситуации ( ветвления ) на диаграмме последовательностей? Да легко (рис. 5.5)!
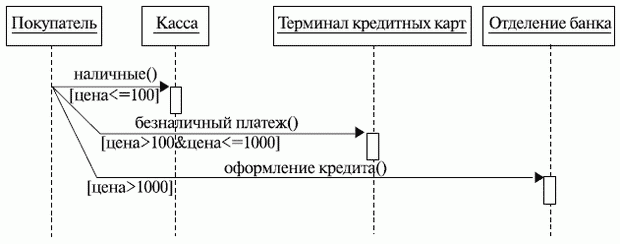
Рис. 5.5.
Впрочем, ветвление - конструкция для диаграмм последовательностей непопулярная и используется она в них очень редко. Считается, что ветвления более присущи диаграммам деятельностей...
Ранее мы говорили, что сообщение посылается объектом в расчете на определенную реакцию, на то, что за этим последует некоторая деятельность. Например, посылка ответного сообщения. А как на диаграммах последовательностей изображаются ответные сообщения? Обычно их изображают пунктирной линией со стрелкой, хотя часто они имеют точно такой же вид, как и обычные сообщения, только направлены в противоположную сторону. Как именно их рисовать - пунктирной линией или сплошной - решать вам. Это абсолютно не принципиально (рис. 5.6).

Рис. 5.6.
Хм, картина усложняется. Мы уже видели два вида стрелок. И соответственно, два вида сообщений - прямое и ответное. Может быть, есть еще какие-то виды сообщений, о которых мы пока не знаем? Да, есть. Сами по себе сообщения бывают синхронными и асинхронными. Синхронные сообщения приостанавливают поток выполнения до тех пор, пока не будет получен ответ. Все сообщения, которые мы рассматривали в наших примерах, были именно синхронными. Пусть мы и не везде рисовали ответное сообщение, но оно подразумевалось: банк выносит решение о предоставлении кредита и сообщает его вам, терминал кредитных карт подтверждает транзакцию и печатает чек, на котором вы ставите подпись, кассир выдает вам подтверждение платежа - кассовый чек. Синхронные сообщения изображаются сплошной линией с треугольной закрашенной стрелкой на конце.
Другой вид сообщений - асинхронные сообщения. Они не ждут ответа, не приостанавливают поток выполнения - сразу после их посылки происходит немедленный переход к следующему шагу, и последовательность продолжается. Входя в офис поутру и говоря коллегам "hello, how are you?", вы ведь не ждете, что они остановят вас и начнут в течение часа рассказывать о своих проблемах? Это просто формальное приветствие, не предусматривающее ответа (асинхронное). Асинхронные сообщения изображаются сплошной линией с обычной (составленной из двух отрезков) стрелкой на конце. А как изображаются ответные сообщения, мы уже знаем (рис. 5.7):
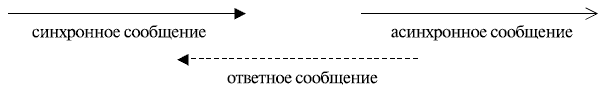
Рис. 5.7.
И еще. Возможны случаи, когда нам известен адресат сообщения, но неизвестен его отправитель. С примерами таких сообщений (в бумажном виде) в советские времена довольно часто встречались секретари госучр
Дата добавления: 2015-02-09; просмотров: 1501; Мы поможем в написании вашей работы!; Нарушение авторских прав |