
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основы гидростатики 2.1. Силы, действующие в жидкости
Поскольку жидкость обладает свойством текучести и легко деформируется под действием минимальных сил, то в жидкости не могут действовать сосредоточенные силы, а возможно существование лишь сил распределённых по объёму (массе) или по поверхности. В связи с этим действующие на жидкости распределённые силы являются по отношению к жидкости внешними. По характеру действия силы можно разделить на две категории: массовые силы и поверхностные.
Массовые силы пропорциональны массе тела и действуют на каждую жидкую частицу этой жидкости. К категории массовых сил относятся силы тяжести и силы инерции переносного движения. Величина массовых сил, отнесённая к единице массы жидкости, носит название единичной массовой силы. Таким образом, в данном случае понятие о единичной массовой силе совпадает с определением ускорения. Если жидкость, находится под действием только сил тяжести, то единичной силой является ускорение свободного падения:

где М' - масса жидкости
Если жидкость находится в сосуде, движущимся с некоторым ускорением а, то жидкость в сосуде будет обладать таким же ускорением (ускорением переносного движения):

Поверхностные силы равномерно распределены по поверхности и пропорциональны площади этой поверхности. Эти силы, действуют со стороны соседних объёмов жидкой среды, твёрдых тел или газовой среды. В общем случае поверхностные силы имеют две составляющие нормальную и тангенциальную. Единичная поверхностная сила называется напряжением. Нормальная составляющая поверхностных сил называется силой давления Р, а напряжение (единичная сила) называется давлением:
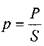 5
5
где: S - площадь поверхности.
Напряжение тангенциальной составляющей поверхностной силы Т (касательное напряжение  ) определяется аналогичным образом (в покоящейся жидкости Т=0).
) определяется аналогичным образом (в покоящейся жидкости Т=0).
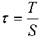
Величина давления (иногда в литературе называется гидростатическим давлением) в системе СИ измеряется в паскалях.
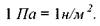
Поскольку эта величина очень мала, то величину давления принято измерять в мега-паскалях МПа
1МПа = \ 106 Па.
В употребляемой до сих пор технической системе единиц давление измеряется в технических атмосферах, am. С,
1 am = \кГ/см2 = 0,1 МПа, 1 МПа = 10 am.
В технической системе единиц давление кроме технической атмосферы измеряется также в физических атмосферах, А.
\А = 1,033 am.
Различают давление абсолютное, избыточное и давление вакуума. Абсолютным давлением называется давление в точке измерения, отсчитанное от нуля. Если за уровень отсчёта принята величина атмосферного давления, то разница между абсолютным давлением и атмосферным называется избыточным давлением.

Если давление, измеряемое в точке ниже величины атмосферного давления, то разница между замеренным давлением и атмосферным называется давлением вакуума

Избыточное давление в жидкостях измеряется манометрами. Это весьма обширный набор измерительных приборов различной конструкции и различного исполнения. 2.2. Свойства гидростатического давления
В неподвижной жидкости возможен лишь один вид напряжения - напряжение сжатия. Как отмечалось ранее, жидкость в общем случае может находиться под действием двух сил - силы давления равномерно распределённой по всей внешней поверхности выделенного жидкого тела и массовых сил, определяемых характером переносного движения. Под внешней границей жидкого тела могут пониматься как соседние тела: твёрдые (стенки сосуда или трубы, в которые помещена жидкость), газообразные (поверхность раздела между жидкостью и газовой средой), так и условные поверхности, мысленно выделяемые внутри самой жидкости. Действующее на внешнюю поверхность жидкости давление обладает двумя основными свойствами: t
1. Давление всегда направлено по внутренней нормали к выделенной поверхности. Это свойство вытекает из самой сущности давления и доказательств не требует. Тем не менее, поясним этот постулат простым примером. Отсечём от жидкого тела часть его объ-
ёма и для сохранения равновесия оставшейся части жидкости приложим к образовавшемуся сечению систему распределённых сил. По своей величине и напрвлению действия эти силы должны обеспечить эк  вивалентное влияние на оставшийся объём жидкости со стороны отсечённой части жидкого тела. Поскольку в покоящейся
вивалентное влияние на оставшийся объём жидкости со стороны отсечённой части жидкого тела. Поскольку в покоящейся
жидкости не могут существовать касательные напряжения, то приложенные к сечению силы могут быть направлены лишь по внутренней нормали к площади сечения.
2. В любой точке внутри жидкости давление по всем направлениям одинаково. Другими словами величина давления в точке не зависит от ориентации площадки, на которую действует давление.
Для доказательства этого положения выделим в районе произвольно выбранной точки находящейся внутри жидкости малый отсек жидкости в виде тетраэдра. Три взаимно перпендикулярные грани отсека будут параллельны координатным плоскостям, четвёртая грань расположена под произвольным углом (по отношению к одной из координатных плоскостей). От 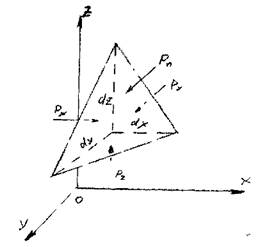 бросим массу жидкости, находящуюся с внешней стороны поверхности тетраэдра, а действие
бросим массу жидкости, находящуюся с внешней стороны поверхности тетраэдра, а действие
отброшенной массы жидкости на выделенный отсек заменим силами, которые обеспечат равновесие в покоящейся жидкости. При такой замене мы сделали некоторое допущение, ввели сосредоточенные силы, действующие на грани отсека. Однако это допущение мож- . но считать справедливым ввиду малости отсека. Тогда для обеспечения равновесия на отсек жидкости должны действовать силы давления нормальные к граням отсека 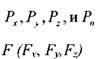 ; корме того, на этот же отсек жидкости будут действовать массовые силы
; корме того, на этот же отсек жидкости будут действовать массовые силы
характер действия которых определяется переносным движением, т.е. движением сосуда, относительно которого покоится жидкость. Величина массовых сил будет
пропорциональна массе жидкости в отсеке: 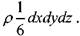
Запишем уравнение равновесия отсека жидкости в проекциях на оси координат.
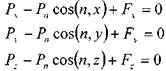
Выразив силы через напряжения, уравнения равновесия будут иметь следующий вид:
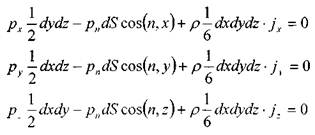
где: 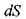 - площадь наклонной грани отсека,
- площадь наклонной грани отсека, 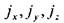 - проекции ускоре-
- проекции ускоре-
ния переносного движения на оси координат.
учитывая, что: 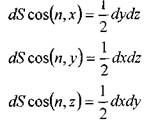
Уравнения равновесия примут вид:
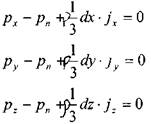
Пренебрегая малыми величинами, получим: 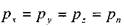
3. Для жидкости находящейся в состоянии равновесия справедлив так называемый закон Паскаля утверждающий, что всякое изменение давления в какой-либо точке жидкости передаётся мгновенно и без изменения во все остальные точки жидкости.
Дата добавления: 2015-02-09; просмотров: 269; Мы поможем в написании вашей работы!; Нарушение авторских прав |