Методы анализа электрических цепей постоянного тока

Понятие анализа электрических цепей. Анализ резистивных цепей заключается в следующем: даны электрическая цепь и значения всех элементов, требуется рассчитать токи во всех ветвях.

Поскольку никаких других законов, кроме законов Ома и Кирхгофа, для электрических цепей не существует, то все рассматриваемые далее методы анализа основаны на этих законах и отличаются лишь формами и, возможно, количеством исходных уравнений.

Существует несколько методов расчета параметров электрических цепей. Особенностью этих методов является применимость их не только к цепям постоянного, но и переменного тока, не только к линейным, но и нелинейным цепям. Здесь мы рассмотрим применение этих методов к линейным цепям постоянного тока, а особенности их применения в цепях других типов рассмотрим при изучении этих цепей.

Метод трансфигурации электрической цепи (метод Кеннели). Метод применим для электрических цепей с одним источником питания. Путем последовательных упрощений всю пассивную часть такой цепи можно заменить одним эквивалентным резистором и вычислить входной ток, а затем, раскрывая схему в обратном направлении, найти все оставшиеся токи.

Принцип расчета электрической цепи методом трансфигурации схемы (методом эквивалентных сопротивлений) рассмотрим на примере схемы двухполюсника, представленной на рисунке 2.29. Для этой схемы определим входное сопротивление, токи в ветвях и напряжения на сопротивлениях.

a b c

Рис. 2.29. Электрическая цепь

Схема (рис. 2.29, a) может быть преобразована следующим образом.

Резисторы R2 и R3 соединены параллельно. Их эквивалентное сопротивление можно найти по формуле:

.

После определения R₂₃ схема на рисунке 2.29, a преобразуется в схему, приведенную на рисунке 2.29, b. В этой схеме все резисторы соединены последовательно. Входное (или эквивалентное) сопротивление схемы определяется по формуле:

. (2.7)

Таким образом, исходная схема преобразована в эквивалентную схему (рисунок 2.29, c), сопротивление которой определяется по формуле (2.7).

Входной ток

.

По второму закону Кирхгофа составим уравнение напряжений для первого (внутреннего контура) (рис. 2.29, a), чтобы найти напряжение U_ab:

R₁I₁ + U_ab + R₄I₁ − U = 0.

Из этого уравнения:

U_ab = U − (R₁ + R₄)I₁,

где I₁ вычисляется по (2.7) для заданных значений

напряжения и сопротивлений.

Зная напряжение U_ab, можно определить токи I₂ и I₃

, .

и падения напряжения на резисторах:

U₁ = R₁I₁, U₄ = R₄I₁.

Метод непосредственного использования законов Кирхгофа. Законы Кирхгофа дают возможность анализа разветвленных электрических цепей. Для этого произвольно назначаются положительные направления токов в отдельных ветвях и составляется ряд уравнений по первому и второму законам Кирхгофа для узлов и контуров схемы цепи. Для электрической цепи, содержащей n ветвей между m узлами нужно определить n токов. Для m узлов по первому закону Кирхгофа можно составить m – 1 независимых уравнений токов, остальные n – (m – 1) независимых уравнений по второму закону Кирхгофа составляются для контуров цепи. Последние уравнения будут независимыми, если в каждый следующий контур будет входить хотя бы одна ветвь, не входившая в предыдущие контуры.

Пример 2.6. Рассмотрим применение метода для следующей цепи.

Нужно определить все токи, если известны значения J, E₁, E₃, R₁, R₂, R₃.

Решение.

1. Выявим узлы (а и b) и ветви.

2. Направим токи I₁, I₂, I₃. Ток источника тока уже обозначен и известен.

Определим число расчетных уравнений:

m − m_J = 4 – 1 = 3.

3. Составим (n − 1) = 2 − 1 = 1 уравнение по первому закону Кирхгофа:

J + I₁ − I₂ − I₃ = 0

либо

I₁ − I₂ − I₃ = −J.

4. Дописываем два недостающих уравнения по второму закону Кирхгофа. Рекомендуется составлять уравнения для «главных», не содержащих в себе других контуров. Направление обхода разных контуров может быть произвольным.

U₁ + U₂ = E₁;

−U₂ + U₃ = E₃.

Подставив выражения напряжений по закону Ома, получим следующую систему уравнений:

5. Решением системы находим токи.

■

Рассмотренный пример дает возможность определить последовательность действий при анализе электрических цепей непосредственным использованием уравнений Кирхгофа.

План анализа:

1. Произвольно выбрать направления всех токов в ветвях на исходной схеме.

2. Определить общее количество уравнений, которые необходимо составить по первому

N_ЗК1 = m – 1

и второму

N_ЗК2 = n – m + 1 – N_т,

законам Кирхгофа, где

N_ЗК1 – количество уравнений по первому закону Кирхгофа;

N_ЗК2 – количество уравнений по второму закону Кирхгофа.

m – число узлов;

n – число ветвей;

N_т – число источников тока;

3. Записать N_ЗК1 уравнений по первому закону Кирхгофа для постоянных токов

где р – число токов в узле;

I_k – ток в ветви k.

Ток I_k пишется со знаком + , если он направлен от узла и –I_k – если к узлу (или все наоборот).

4. Записать N_ЗК2 уравнений по второму закону Кирхгофа для постоянных величин

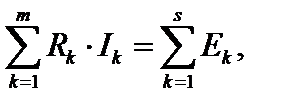
гдеm – число ветвей в контуре;

s – число источников ЭДС в контуре;

R_k – общее сопротивление ветви k.

ЭДС пишется со знаком "плюс", если направление обхода выбранного контура совпадает с направлением ЭДС, и "минус", если не совпадает. Падение напряжения R_k×I_k записывают со знаком "+", если направление обхода выбранного контура совпадает с направлением тока I_k, и со знаком "–", если не совпадает.

5. Получившуюся систему уравнений решить относительно токов.

Замечание. Следует помнить, что второй закон Кирхгофа в резистивных и только в резистивных цепях справедлив также для действующих, максимальных, амплитудных значений.

Примечание. При расчете электрических цепей ток рассматривается в алгебраическом смысле, причем положительное направление выбирается произвольно. Если после вычислений значение тока получается отрицательным, то это означает, что этот ток направлен против выбранного положительного направления, если ток – положителен, то этот ток течет по ранее выбранному направлению.

Систему уравнений по законам Кирхгофа можно записать в матричной форме следующим образом:

[А]⋅[I ]= [F],

где [А] – квадратная матрица коэффициентов;

[I ] – матрица-столбец неизвестных токов ветвей;

[F] – матрица-столбец активных параметров, которыми являются токи источников тока и ЭДС.

Уравнения в системе не однотипны, так как записаны на основании двух разных законов. В уравнениях по первому закону Кирхгофа коэффициенты a_ij безразмерны и могут принимать значения ±1 или 0, а в правой части

F_j = ΣJ .

F_i = ΣE .

В уравнениях по второму закону Кирхгофа коэффици-енты a_ij имеют размерность сопротивления

Если j-я ветвь входит в i-й контур, для которого составлено уравнение, то

a_ij = ±R_ij ,

если не входит, то

a_ij = 0 .

Для рассмотренного примера

Рассмотрим еще один пример.

Пример. 2.7. Покажем применение метода уравнений Кирхгофа на примере схемы, изображенной на рисунке.

Произвольно задавшись направлениями токов в ветвях и принимая токи, подтекающие к узлу, положительными, а оттекающие от узла – отрицательными, записываем:

(2.8)

Число независимых уравнений в первом законе Кирхгофа – на единицу меньше числа узлов, поэтому для последнего узла d уравнение не пишем.

В заданной схеме семь ветвей, семь неизвестных токов. Система (2.8) содержит только три уравнения. Недостающие четыре записываем по второму закону Кирхгофа.

Число уравнений, составляемых по этому закону, равно числу взаимно независимых контуров. При рассмотрении схемы каждый последующий контур является независимым относительно предыдущих, если он отличается от них хотя бы одной новой ветвью.

В заданной схеме таких контуров четыре. Они отмечены пронумерованными дугообразными стрелками. Любой другой контур новых ветвей не содержит, поэтому не является независимым. Дугообразные стрелки показывают произвольно выбранные направления обхода контуров. Если направления ЭДС и токов совпадают с направлением обхода контура, то они записываются с плюсом, если не совпадают – то с минусом.

(2.9)

Системы (2.8) и (2.9) дают достаточное количество уравнений для отыскания всех неизвестных токов.

■

Расчет по законам Кирхгофа является универсальным, но громоздким. Поэтому на его основе разработаны методы, позволяющие упростить решение.

Метод узловых потенциалов. Ток в любой ветви электрической цепи можно определить по известным потенциалам узлов этой ветви. Поэтому если определить неизвестные потенциалы узлов цепи, то токи могут быть легко определены на основе закона Ома.

Уравнения, составляемые по этому методу, называются

узловыми уравнениями. Их число значительно сокращается по сравнению с числом уравнений в методе уравнений Кирхгофа, за счет применении первого закона Кирхгофа и обобщенного закона Ома.

В качестве неизвестных они содержат потенциалы узлов, причем один из них задается заранее – обычно принимается равным нулю. Рационально заземлять узел, в котором сходится максимальное число ветвей.

По найденным значениям потенциалов с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей дерева n.

Распределение потенциала в электрической цепи. Потенциальная диаграмма.Определим потенциалы точек 1, 2, 3, 4, 5вдоль замкнутого контура электрической цепи на рис. 2.30.

Рис. 2.30. Электрическая цепь

Составим уравнение напряжений по второму закону Кирхгофа для замкнутого контура:

E₂− E₁ = U₁ + U₂ + U₃,

где U₁ = R₁I , U₂ = R₂I , U₃ = R₃I .

Направление тока I соответствует E₂ > E₁.

ЭДС и напряжения выражаются через потенциалы следующим образом:

E₁ = j₂ − j₃.

E₂ = j₁ − j₅.

U₁ = j₃ − j₄. (2.10)

U₂ = j₄ − j₅.

U₃ = j₁ − j₂.

Примем потенциал одной из точек, например, точки 4, равным нулю. Распределение потенциала относительно нулевого потенциала точки 4определим на основании уравнений (2.10):

;

;

;

;

;

.

Полученное распределение потенциала относительно нулевой точки можно изобразить графически в виде потенциальной диаграммы. На ней по оси абсцисс откладывают значения сопротивлений вдоль контура, начиная с точки 4, а по оси ординат – значения потенциалов выделенных точек. Потенциальная диаграмма электрической цепи, приведенной на рис. 2.30 показана на рис 2.31.

Рис. 2.31. Потенциальная диаграмма

В практических случаях одна из точек электрической цепи (на рисунке 2.30 – точка 4) может быть соединена с корпусом электроустановки или заземлена, например, в случае пробоя изоляции в точке 4 на заземленный корпус. Это не повлияет на распределение потенциала в цепи, если вся остальная часть цепи имеет хорошую изоляцию. Электрический ток возникает лишь в замкнутой цепи. Заземление одной точки цепи не создаст нового замкнутого пути для тока. Ток на корпус или в заземляющее устройство ответвляться не будет.

Если же появится соединение с корпусом или с заземляющим устройством одновременно в двух точках цепи, то возникнет параллельная ветвь, и распределение потенциала изменится.

Описание метода. Пусть имеем схему, изображенную на рис. 2.32, в которой примем .

Рис. 2.32. Схема электрической цепи

Допустим, что и известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС

,

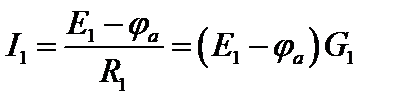
Запишем уравнение по первому закону Кирхгофа для узла а:

и подставим значения входящих в него токов, определенных выше:

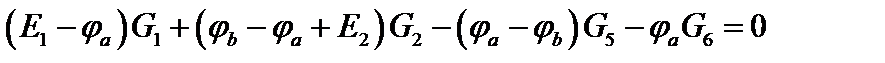
Сгруппировав соответствующие члены, получим:

Аналогично можно записать для узла b:

Приведенная последовательность действий позволяет предложить формальные правила составления узловых уравнений:

1. В левую часть уравнения для i-го узла записываются со знаком «+» произведение потенциала φ_i этого узла на сумму проводимостей G_ii присоединенных к нему ветвей и со знаком «–» – произведения потенциалов φ_j соседних узлов на сумму проводимостей ветвей, соединяющих i-й узел с j-м.

2. В правую часть уравнения для i-го узла записываются со знаком «+» произведения направленных к нему ЭДС присоединенных ветвей на проводимости этих ветвей, и со знаком «–» – аналогичные произведения для ЭДС, направленных от него. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

Составленная таким образом система уравнений имеет следующий обобщенный вид:

где G₁₁, G₂₂, ..., G_mm – собственные проводимости узлов, равные сумме проводимостей ветвей, соединяющихся в соответствующем узле;

G₁₂, G₂₁, G₁₃, ... – общие проводимости между двумя узлами, равные сумме проводимостей ветвей, соединяющих эти узлы;

J₁₁, J₂₂, ..., J_mm – узловые токи, равные алгебраической сумме произведений проводимостей активных ветвей на ЭДС этих ветвей и токов источников тока, соединяющихся в этом узле. С положительным знаком берут ЭДС и токи, направленные к узлу.

На основе проведенного рассмотрения можно сформулировать процедуру анализа электрической цепи методом узловых потенциалов.

План анализа:

1. Произвольно выбрать направления всех токов в ветвях на исходной схеме.

2. Пронумеровать узлы на исходной схеме. Положить равным нулю потенциал последнего узла. Определить количество уравнений N системы уравнений

N=N_у – N_и – 1,

где N_у – число узлов;

N_и – число ветвей, содержащих только идеальные источники ЭДС.

Составить и решить систему уравнений относительно потенциалов узлов j_i

,

гдеG_ss – сумма проводимостей ветвей, присоединенных к узлу s, не содержащих источников тока;

G_sq – сумма проводимостей ветвей, непосредственно соединяющих узел s с узлом q;

– алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу s, на их проводимости.

– алгебраическая сумма источников тока, присоединенных к узлу s.

4. Вычислить токи из обобщенного закона Ома или первого закона Кирхгофа.

Пример 2.8. Составим систему уравнений для схемы на рисунке, приняв φ₄ = 0.

Решением системы уравнений определим потенциалы узлов. Затем рассчитаем токи ветвей по закону Ома:

I₁ = G₁(φ₄ − φ₁ + E₁) = G₁(− φ₁ + E₁),

так как φ₄ = 0,

I₂ = − G₂φ₁;

I₃ = G₃(φ₁ − φ₂ − E₃);

I₄ = G₄( −φ₃ + E₄);

I₅ = G₅(φ₂ − φ₃);

I₆ = G₆(φ₂ − φ₃ − E₆).

■

Метод двух узлов. Этот метод является частным случаем метода узловых потенциалов и применим для схемы с двумя узлами.

Так как потенциал одного из узлов принимают равным нулю, то потенциал второго узла равен напряжению между этими узлами.

Формулу для определения напряжения между двумя узлами в общем виде можно записать следующим образом:

где G_i − проводимости ветвей;

n − число ветвей, содержащих источники ЭДС с отличными от нуля проводимостями;

m − число ветвей, содержащих источники тока;

l − число ветвей без источников тока.

Число слагаемых в числителе равно числу активных ветвей. С положительным знаком записывают Е и J, направленные к первому в индексе напряжения узлу.

Сумма в знаменателе формулы – арифметическая.

Вычислив напряжение между двумя узлами, по закону Ома для ветви находят токи.

Метод контурных токов.Число уравнений, подлежащих решению, в ряде случаев также можно значительно сократить, используя метод контурных токов, основанный на применении второго закона Кирхгофа и обобщенного закона Ома.

Здесь для каждого из взаимно независимых контуров назначается так называемый контурный ток, замыкающийся по всем ветвям контура. Направления этих токов произвольны. Для них составляется система уравнений по второму закону Кирхгофа, решение которой дает значения этих токов. Число уравнений по первому закону Кирхгофа определяется как

,

а по второму – как

,

где m – число узлов цепи, n – число ветвей, а N_m - число источников тока.

Токи ветвей цепи представляют собой алгебраическую сумму контурных токов смежных контуров, поэтому определяются путем сложения или вычитания соответствующих контурных токов.

План анализа:

1. Произвольно выбрать направления всех токов в ветвях на исходной схеме.

2. Выбрать

N_К = n – m + 1 – N_т

независимых контуров, где n – число ветвей, m – число узлов, N_т – число источников тока.

Обозначить контурные токи I_i так, чтобы каждый из них проходил через один источник тока, а оставшиеся N_К выбирают проходящими по ветвям, не содержащим источников тока.

3. Обходя каждый из независимых контуров в выбранном направлении, записать уравнения по второму закону Кирхгофа и решить их относительно контурных токов.

где R_nn – сумма сопротивлений всех ветвей контура n, т.е. собственное сопротивление контура n.

R_n – общее сопротивление ветви контура n с контуром, содержащим источник тока J.

R_ns – общее сопротивление контуров n и s, общее сопротивление контуров записывается со знаком "плюс", если контурный ток I_nn совпадает по направлению с контурным током I_ss, иначе со знаком "минус".

E_nn – алгебраическая сумма ЭДС контура n. ЭДС записывается со знаком "плюс", если контурный ток I_nn совпадает по направлению с направлением ЭДС, иначе со знаком "минус".

4. Вычислить истинные токи во всех ветвях, используя первый закон Кирхгофа, как алгебраическую сумму контур-ных токов, протекающих по данной ветви

I_n = ΣI_nn.

Контурный ток I_nn записывают со знаком «+», если он совпадает по направлению с током I_n, и со знаком «−» − если не совпадает.

Пример 2.9. Рассмотрим применение этого метода для цепи, рассмотренной в предыдущем примере. Ее изображение отличается наличием обозначений для контурных токов I_K1 – I_K4, обозначенных дугообразными стрелками.

Для выбранных контурных токов записываются уравнения по второму закону Кирхгофа. Контур при этом обходится по направлению контурного тока. Рассмотрим порядок составления уравнения на примере третьего контура. Контурный ток I_K3, протекая по сопротивлениям своего контура, создает на них падение напряжения

(2.11)

По сопротивлению R₄, являющемуся элементом третьего контура, протекает контурный ток I_K2. Создаваемое им падение напряжения I_K2×R₄ вычитается из предыдущего, так как направление тока I_K2 в сопротивлении R₄ противоположно току I_K3. Сопротивление R₆ также входит в третий контур. Падение напряжения на нем, создаваемое контурным током I_K4, складывается с суммой (2.11), так как направления I_K4 и I_K3 в R₆ одинаковы. В правой части уравнения записывается алгебраическая сумма всех ЭДС контура, в данном случае – единственная ЭДС E₄.

Итак, для третьего контура имеем:

Аналогично составляются и остальные контурные уравнения:

После решения последней системы действительные токи ветвей определяются по найденным контурным:

■

Метод наложения. Теорема взаимности. Если рассматривать линейную пассивную электрическую цепь, составленную из сопротивлений, емкостей и индуктивностей (в том числе и связанных), то в соответствии с теоремой взаимности контурный ток k-го контура цепи, вызванный действием единственного независимого источника напряжения, помещенного в i-й контур (рис. 2.33, а), равен контурному току i-го контура, вызванному действием того же источника напряжения, перенесенного из i-й контура в k-й (рис. 2.33, b), причем ориентация источника напряжения, помещенного в какой-либо контур, относительно контурного тока этого же контура в обоих случаях принимается одинаковой.

Рис. 2.33. Электрическая цепь

Для случая, когда внешнее воздействие на цепь задается в виде независимого источника тока, теорема взаимности может быть сформулирована следующим образом.

Если независимый источник тока J, подключаемый к какой-либо паре зажимов линейной пассивной цепи, вызывает на другой паре зажимов напряжение U (рис. 2, а), то этот же источник тока, подключенный ко второй паре зажимов (рис. 2, б), вызовет на первой паре зажимов то же

Рис. 2.34. Электрическая цепь

напряжение U (ориентация источника тока относительно напряжения на зажимах, к которым он подключен, в обоих случаях принимается одинаковой).

Если электрическая цепь удовлетворяет теореме взаимности (в любой формулировке), то говорят, что она обладает взаимностью (обратимостью). Электрические цепи, обладающие взаимностью, называются взаимными (обратимыми). Если электрическая цепь не обладает взаимностью, то она является невзаимной (необратимой). К необратимым цепям относятся, в частности, нелинейные цепи.

Принцип наложения (суперпозиции) состоит в том, что реакция линейных электрических цепей на произвольное внешнее воздействие, представляющее собой линейную комбинацию более простых воздействий, равна линейной комбинации реакций, вызванных каждым из простых воздействий в отдельности.

Из этого принципа следует, что ток или напряжение любой ветви линейной электрической цепи, содержащей наряду с пассивными элементами зависимые и независимые источники тока и напряжения, равны сумме частичных токов или напряжений, вызванных действием каждого из независимых источников в отдельности.

На принципе наложения основан широко используемый на практике метод анализа цепей – метод наложения. Его удобно применять в тех случаях, когда по условиям задачи требуется найти ток или напряжение одной из ветвей цепи, в состав которой входит несколько независимых источников. В этом случае искомый ток (напряжение) представляются в виде суммы частичных токов (напряжений), для определения которых используют схемы замещения цепи, получаемые из исходной схемы путем выключения всех независимых источников, кроме одного, вызывающего соответствующий частичный ток (напряжение). Таким образом, задача анализа сложной цепи, содержащей несколько независимых источников энергии, заменяется рядом более простых задач исследования цепей с одним независимым источником.

Следует обратить внимание на то, то при определении частичных токов выключаются только независимые источники тока или напряжения.

Метод наложения (суперпозиции) целесообразно приме-

нять только для расчета линейных электрических цепей с небольшим количеством источников энергии.

Например, токи в схеме на рис. 2.35, а находятся как алгебраические суммы частичных токов, определяемых из схем 2.35, b и c.

a b c

Рис.2.35. Заданная (а) и расчетные (b, c) схемы цепи

Анализ цепи, приведенной на рис. 2.35 производится в

следующей последовательности. Исключая источник ЭДС Е₂, получаем

Аналогично, исключая источник ЭДС Е₁, получаем

Истинные токи в ветвях

При расчете подобных схем очень удобным оказывается следующий прием. Пусть требуется определить токи в параллельных ветвях при известном суммарном токе (рис. 2.36).

Рис. 2.36. Токи в параллельных ветвях

Из схемы следует:

Из полученной формулы вытекает правило: ток в одной из двух параллельных ветвей равен произведению общего тока на сопротивление соседней ветви, деленному на сумму сопротивлений параллельных ветвей. В соответствии с приведенным правилом для второй ветви схемы, приведенной на рис. 2.36 получим

Применение этого правила избавляет от необходимости определять напряжения U_ab` для отдельных ветвей в схемах на рис. 2.35, b и c. Так, после определения тока I₁, токи I₂ и I₃ можно найти по формулам:

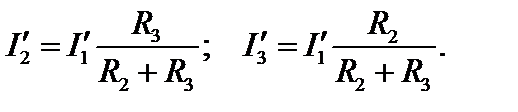
Приведенное рассмотрение дает возможность сформулировать последовательность этапов анализа электрических цепей методом наложения.

План анализа:

1. Произвольно выбрать направления всех токов в ветвях на исходной схеме и пронумеровать все независимые источники целыми числами 1, 2, ...,n.

2. Положить равными нулю все источники ЭДС и тока кроме первого. При этом независимые источники, ЭДС которых равны нулю, заменить короткозамкнутыми отрезками, а независимые источники тока отключают. Если независимые источники имеют внутреннее сопротивление, то эти сопротивления должны оставаться на своих местах в схеме. Все зависимые источники остаются в схеме.

3. В полученной схеме с одним независимым источником любым методом, например методом свертывания, рассчитать все частичные токи .

4. Аналогичным образом рассчитать все частичные токи только от второго источника (все остальные источники полагают равными нулю). Затем только от третьего источника и так далее до .

5. Вычислить истинные токи во всех ветвях на исходной схеме, как алгебраическую сумму всех частичных токов

где i = 1 ... N_в;

N_в – количество ветвей в исходной схеме.

Частичный ток берется со знаком «+», если он совпадает по направлению с истинным током, и «–», если не совпадает.

Метод эквивалентного генератора ЭДС.Этот метод применяется в тех случаях, когда требуется рассчитать ток в какой-либо одной ветви при нескольких значениях ее параметров (сопротивления и ЭДС) при неизменных параметрах всей остальной цепи.

Сущность метода заключается в следующем. Вся цепь относительно зажимов интересующей нас ветви представляется как активный двухполюсник, который заменяется эквивалентным генератором ЭДС, к зажимам которого подключается интересующая нас ветвь. В итоге получается простая неразветвленная цепь, ток в которой определяется по закону Ома.

ЭДС Е_Э эквивалентного генератора и его внутреннее сопротивление R_Э находятся из режимов холостого хода и короткого замыкания двухполюсника.

Теорема компенсации.Теоретическим обоснованиемметода эквивалентного генератора является теорема компенсации, суть которой состоит в следующем. Токи и напряжения ветвей произвольной электрической цепи не изменятся, если любую ветвь этой цепи заменить идеальным источником ЭДС, напряжение которого равно напряжению данной ветви и имеет одинаковое с ним направление, либо идеальным источником тока, ток которого равен току рассматриваемой ветви и совпадает с ним по направлению.

Рассмотрим линейную электрическую цепь, находящуюся под воздействием постоянного тока. Выделим в данной цепи произвольную ветвь, сопротивление которой равно R (рис. 2.37, а).

a b c

Рис. 2.37. Выделенная ветвь произвольной электрической цепи

Напряжение и ток этой ветви связаны уравнением, составленным на основании закона Ома U = RI. В соответствии с теоремой компенсации выделенную ветвь можно заменить идеальным источником ЭДС (рис. 2.37, b), напряжение которого равно напряжению данной ветви E = U = RI и имеет одинаковое с ним направление (ЭДС источника направлена навстречу напряжению ветви), либо идеальным источником тока, ток которого равен току рассматриваемой ветви J = I = U/R и совпадает с ним по направлению (рис. 2.37, c).

Необходимо отметить, что источники напряжения и тока, заменившие согласно теореме компенсации сопротивление ветви R, зависимые: ЭДС источника напряжения E прямо пропорциональна току ветви, содержащей этот источник, а ток источника тока J прямо пропорционален напряжению этой ветви. Точно также идеальный источник напряжения, ЭДС которого E = RI, и идеальный источник тока, ток которого J = U/R, могут быть заменены эквивалентным сопротивлением R = E/I = U/J .

Теорема компенсации расширяет возможности эквива-

лентных преобразований электрических цепей. В частности, ее применение совместно с переносом источников тока или напряжения позволяет производить перенос любых двухполюсных элементов электрической цепи.

Рассмотрим линейную электрическую цепь, которая наряду с идеализированными пассивными элементами содержит управляемые и неуправляемые источники тока и напряжения. Выделим в этой цепи произвольную ветвь ab (рис. 2.38, а), а остальную часть цепи, к которой подключена эта ветвь, представим в виде автономного двухполюсника D.

a b c

Рис. 2.38. Выделенная ветвь произвольной электрической цепи

В соответствии с теоремой о компенсации автономный двухполюсник, к которому подключена данная ветвь, можно заменить эквивалентным линеаризованным источником, который может быть представлен последовательной или параллельной схемами замещения.

ЭДС источника напряжения E_эк в последовательной схеме замещения (рис. 2.38, b) равна напряжению холостого хода автономного двухполюсника, а внутреннее сопро-тивление R_эк равно его входному сопротивлению. Ток идеального источника тока J_эк в параллельной схеме замещения (рис. 2.38, c) равен току короткого замыкания автономного двухполюсника, а внутренняя проводимость Y_эк – его комплексной входной проводимости.

Теорему о компенсации (теорему об эквивалентном источнике) применительно к схеме замещения с источником напряжения часто называют теоремой Гельмгольца или Тевенена, а применительно к схеме замещения с источником тока – теоремой Нортона.

Воспользовавшись теоремой об эквивалентном источнике, можно найти последовательную или параллельную схему замещения любого сколь угодно сложного линейного активного двухполюсника, поэтому данную теорему часто называют теоремой об активном двухполюснике.

Эта теорема позволяет существенно упростить анализ цепей, особенно в тех случаях, когда требуется определить ток или напряжение только одной ветви сложной цепи, содержащей большое число управляемых и неуправляемых источников тока и напряжения. В связи с тем, что параметры элементов последовательной и параллельной схем замещения активного двухполюсника легко поддаются измерениям, выполняемым на внешних зажимах, теорему об эквивалентном источнике применяют и для построения схем замещения активных двухполюсников по результатам их экспериментального исследования.

План анализа:

1. Произвольно выбрать положительное направление искомого тока I в ветви ab на исходной схеме.

2. Составить схему цепи с исключенной из исходной схемы ветвью ab. В получившейся схеме (без ветви ab) вычислить относительно зажимов ab любым методом напряжение холостого хода, направление U_ХХ выбирают произвольно.

Составить равенство E_ЭК = U_ХХ.

3. Составить схему для вычисления R_ЭК. Для этого используют схему п.2, в которой источники ЭДС заменяют короткозамкнутыми отрезками, источники тока отключают. Если источники имеют внутреннее сопротивление, то их сопротивления должны оставаться в схеме. Используя эквивалентные преобразования, вычислить R_ЭК относительно зажимов ab.

4. Составить одноконтурную цепь с подключённой ветвью ab, при этом направление E_ЭК принять противоположным направлению U_ХХ на схеме п. 2.

По закону Ома находят искомый ток

где ΣR_ab – арифметическая сумма сопротивлений всех внешних и внутренних резисторов ветви ab;

ΣE_ab – алгебраическая сумма ЭДС ветви ab,

ЭДС берется со знаком "плюс", если его положительное направление совпадает с направлением тока I, иначе берется со знаком "минус".

Порядок решения задачи этим методом рассмотрим на конкретном числовом примере.

Пример 2.10. В цепи, показанной на рисунке, требуется рассчитать ток I₃ при шести различных значениях резистора R₃ и по результатам расчета построить график зависимости I₃(R₃).

a b

Числовые значения параметров цепи: Е₁ = 225 В; Е₃ = 30 В; R₁ = 3 Ом; R₂ = 6 Ом.

Решение.

а) Расчет режима холостого хода.

Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. а).

Напряжение между ними, равное U_X, находится как падение напряжения на резисторе R₂:

б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. б).

Ток короткого замыкания:

I_k = E₁/R₁ = 75 A.

Внутреннее сопротивление эквивалентного генератора:

R_э = U_x/I_k = 2 Oм.

Величину R_э можно найти и другим способом. Оно равно входному сопротивлению двухполюсника при равенстве нулю всех его ЭДС. Если на рис. а мысленно закоротить зажимы ЭДС Е₁, то резисторы R₁ и R₂ окажутся соединенными параллельно, и входное сопротивление цепи относительно зажимов m и n будет равно:

Ток в полученной неразветвленной цепи (рис. б) определяется по закону Ома:

Подставляя в последнюю формулу требуемые значения резистора R₃, вычисляем ток и строим график.

■

Данную задачу целесообразно решать именно методом эквивалентного генератора. Применение другого метода, например метода контурных токов, потребует решать систему уравнений столько раз, сколько значений тока необходимо найти. Здесь же всю цепь мы рассчитываем только два раза, определяя Е_э и R_э, а многократно используем лишь одну простую формулу (7).

Метод эквивалентного генератора тока. Метод эквивалентного источника тока для анализа резистивных цепей, как и предыдущий метод, будет заключаться в следующем. Дана электрическая цепь и значения всех элементов. Нужно найти только один ток I в заданной ветвиab (рис. 2.39).

Рис. 2.39. Схема электрической цепи

План анализа:

1. Произвольно выбрать положительное направление искомого тока I ветви ab на исходной схеме.

2. Заменить ветвь ab короткозамкнутым отрезком. Направление тока короткого замыкания I_k выбрать совпадающим с направлением токаI. Вычислить любым методом ток I_k. Составить равенство J_ЭК = I_k.

3. Вычислить R_ЭК. Для этого используют схему из п.2, в которой источники ЭДС заменяют короткозамкнутыми отрезками. Источники тока отключают. Если источники имеют внутреннее сопротивление, то их сопротивления должны оставаться в схеме. Используя эквивалентные преобразования, вычислить R_ЭК относительно разомкнутых зажимов ab.

4. Составить цепь с подключённой ветвью ab. При этом направление J_ЭК на схеме должно быть противоположным с направлениемI_k в схеме из п.2.

5. Используя метод уравнений Кирхгофа, найти искомый ток

где ΣR_ab – арифметическая сумма всех внешних и внутренних сопротивлений ветвиab;

ΣE_ab – алгебраическая сумма ЭДС ветви ab, ЭДС берется со знаком "плюс", если его положительное направление совпадает с направлением тока I, иначе берется со знаком "минус".

Пример 2.11. Определить значение тока I₂ в цепи методом эквивалентного источника тока при Е₁ = 1 В, Е₂ = 3 В, Е₃ = 5 В, R₁ = 2 Ом, R₂ = 4 Ом, R₃ = 2 Ом.

Решение. Разделим схему на две части, границей для которых будут точки a и b. Одна часть схемы содержит резистор R₂, ток через которой подлежит определению, а вторая – представляет собой активный двухполюсник.

Произведем замену активного двухполюсника на источник напряжения. Для этого необходимо определить значения Е_ЭК и R_ЭК. Начнем с Е_ЭК.

Далее определяем значение R_эк для заданной цепи со стороны контактов а и b.

Производим замену активного двухполюсника на эквивалентный источник напряжения с рассчитанными параметрами:

■

Пример 2.12. Определить величину тока I₃ методом эквивалентного источника при J = 50 мА, Е = 60 В, R₁ = 5 кОм, R₂ = 16 кОм, R₃ = 8 кОм, R₄ = 4 кОм, R₅ = 2 кОм.

Решение. Разделим электрическую цепь на две части относительно точек а и b. Одна часть состоит из резистора R3, а вторая – из всех остальных элементов цепи. Она представляет собой активный двухполюсник.

Произведем замену активного двухполюсника на источник напряжения. Для этого необходимо определить значения Е_эк и R_эк.

Величину Е_эк проще всего в данном случае определить методом узловых потенциалов (точнее, методом двух узлов):

Теперь определим R_ЭК относительно контактов а и b.

Производим замену активного двухполюсника на эквивалентный источник напряжения:

■