
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема. Кинематика и динамика вращательного движения твердого тела. Закон сохранения момента импульса.
План
1. Вращение твердого тела.
2. Угловая скорость. Связь линейной скорости м угловой.
3. Период и частота вращения.
4. Угловое ускорение.
5. Связь тангенциального и нормального ускорения с угловой скоростью и угловым ускорением.
6. Кинематические уравнения вращательного движения.
7. Основные динамические величины: момент силы, момент инерции, момент импульса.
8. Законы динамики вращательного движения твердого тела.
9. Кинетическая энергия тела, которое вращается.
 1 Вращением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения тела, и описывают круги, центры которых лежат на этой оси.
1 Вращением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения тела, и описывают круги, центры которых лежат на этой оси.
Пусть некоторая точка А движется по кругу радиуса R. Все точки радиуса поворачиваются в течение времени Δt на одинаковый угол Δφ. Мерой перемещения всего тела за малый промежуток времени dt служит вектор  элементарного поворота тела. Модуль вектора
элементарного поворота тела. Модуль вектора  равен углу поворота тела и направлен вдоль оси вращения по правилу правого винта: с конца вектора
равен углу поворота тела и направлен вдоль оси вращения по правилу правого винта: с конца вектора  поворот тела происходит против хода часовой стрелки.
поворот тела происходит против хода часовой стрелки.
2 Кинематической характеристикой направления и скорости вращения тела служит угловая скорость.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:


Вектор  направлен вдоль оси вращения так, что с его конца вращение видно против движения стрелки часов.
направлен вдоль оси вращения так, что с его конца вращение видно против движения стрелки часов.
Линейная скорость точки А 
3. Если за время t тело осуществляет N оборотов, то время, в течение которого вращающееся тело осуществляет один полный оборот  , называется периодом вращения. С другой стороны, тело, которое равномерно вращается с угловой скоростью ω, за время Т поворачивается на угол φ=2π. Поэтому
, называется периодом вращения. С другой стороны, тело, которое равномерно вращается с угловой скоростью ω, за время Т поворачивается на угол φ=2π. Поэтому  .
.
Количество оборотов за единицу времени называется частотой вращения:  .
.
При равномерном вращении  .
.
4. Вектор  может изменяться как за счет изменения скорости вращения тела вокруг оси (в таком случае он изменяется по величине), так и за счет поворота оси вращения в пространстве (в таком случае он изменяется по направлению). Изменение вектора угловой скорости со временем характеризуется угловым ускорением.
может изменяться как за счет изменения скорости вращения тела вокруг оси (в таком случае он изменяется по величине), так и за счет поворота оси вращения в пространстве (в таком случае он изменяется по направлению). Изменение вектора угловой скорости со временем характеризуется угловым ускорением.
Средним угловым ускорением  называется физическая величина равная отношению изменения угловой скорости
называется физическая величина равная отношению изменения угловой скорости  к промежутку времени
к промежутку времени  , за которое это изменение произошло:
, за которое это изменение произошло: 
Мгновенным угловым ускорением  называется граница среднего углового ускорения:
называется граница среднего углового ускорения: 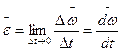 .
.
Итак, угловое ускорение равно первой производной по времени от угловой скорости. Угловое ускорение, как и угловая скорость, является псевдовектором.
5. Определим тангенциальное и нормальное ускорение точки А вращающегося тела через угловую скорость и угловое ускорение:


1При равнопеременном вращении (ε = const) из выражения  получаем:
получаем: 
 ω = ω0 + εt
ω = ω0 + εt
где ω0 – начальная угловая скорость.

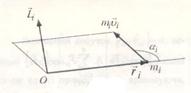
7. Для характеристики внешнего механического действия на тело, которое приводит к изменению вращательного движения тела, вводится понятие момента силы.
Моментом силы  относительно неподвижной точки О называется векторное произведение радиус-вектора
относительно неподвижной точки О называется векторное произведение радиус-вектора  , который проведен из точки О в точку приложения силы, на силу
, который проведен из точки О в точку приложения силы, на силу  :
:  .
.
 Вектор
Вектор  направлен перпендикулярно к плоскости
направлен перпендикулярно к плоскости
векторов  и
и 
Модуль момента силы 
где  – угол между
– угол между  и
и  ,
, 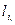 =
=  – плечо силы – длина перпендикуляра, опущенного из точки О на линию действия силы
– плечо силы – длина перпендикуляра, опущенного из точки О на линию действия силы 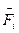 .
.
Моментом импульса  материальной точки относительно неподвижной точки О называется векторное произведение радиус-вектора
материальной точки относительно неподвижной точки О называется векторное произведение радиус-вектора  материальной точки, который проведен из точки О, на импульс этой материальной точки
материальной точки, который проведен из точки О, на импульс этой материальной точки  :
:  .
.
Моментом импульса тела относительно неподвижной оси называется скалярная величина  , которая равна проекции на эту ось вектора момента импульса тела относительно произвольной точки О на оси ОZ.
, которая равна проекции на эту ось вектора момента импульса тела относительно произвольной точки О на оси ОZ.
Сумма произведений масс всех материальных точек тела на квадраты их расстояний до оси ОZ называется моментом инерции тела относительно этой оси:  . Итак, Lz=jzωz/
. Итак, Lz=jzωz/
Момент импульса тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость вращения вокруг этой оси.
L = J*ω
Основной закон динамики вращательного движения:Скорость изменения момента импульса тела, которое вращается вокруг неподвижной точки, равна главному моменту относительно этой точки всех внешних сил, которые приложены к телу.
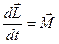 ,
,
где  – момент импульса тела относительно точки О, а
– момент импульса тела относительно точки О, а 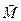 – главный момент внешних сил относительно точки О.
– главный момент внешних сил относительно точки О.
Из уравнения динамики тела, которое вращается вокруг неподвижной оси OZ, вытекает закон сохранения момента импульса тела относительно этой оси:
если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется во время движения:
 и
и  ,
,  ,
,
или
 ,
,
где  – угловая скорость тела,
– угловая скорость тела,  – его момент инерции относительно оси вращения.
– его момент инерции относительно оси вращения.
 Полученное соотношение наглядно иллюстрируется с помощью лавки Жуковского – круглой платформы, которая может вращаться с малым трением относительно вертикальной оси (рис. 8). Если гантели приближаются к оси вращения, то момент инерции системы уменьшается, а угловая скорость увеличивается, при отдалении гантелей от оси вращения угловая скорость вращения уменьшается (І2>І1; ω2<ω1).
Полученное соотношение наглядно иллюстрируется с помощью лавки Жуковского – круглой платформы, которая может вращаться с малым трением относительно вертикальной оси (рис. 8). Если гантели приближаются к оси вращения, то момент инерции системы уменьшается, а угловая скорость увеличивается, при отдалении гантелей от оси вращения угловая скорость вращения уменьшается (І2>І1; ω2<ω1).
Закон сохранения момента импульса – фундаментальный закон природы. Он связан с определенными свойствами симметрии пространства – его изотропностью, то есть с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.
9. Если твердое тело движется поступательно со скоростью υ и одновременно вращается с угловой скоростью ω вокруг оси, которая проходит через его центр инерции, то его кинетическая энергия
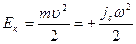 .
.
Контрольные вопросы
1. Что называется вращением абсолютно твердого тела вокруг неподвижной оси?
2. Что называется моментом инерции? Является ли эта величина векторной?
3. Какой принцип лежит в основе вычисления момента инерции произвольного тела?
4. Запишите динамические уравнения поступательного и вращательного движений. Что общего и в чем разница между этими уравнениями?
5. Что называется моментом импульса? Что характеризует эта величина? Для чего она вводится?
6. Сформулируйте закон сохранения момента импульса. Когда он выполняется? Приведите примеры.
7. Как вычислить кинетическую энергию тела, которое вращается? В чем заключается физический смысл кинетической энергии? В чем заключается физический смысл каждой из величин, входящих в формулу кинетической энергии тела, которое вращается. Какие величины аналогичны им в формуле кинетической энергии поступательного движения?
8. Как объяснить существование нарезного и простого огнестрельного оружия? В чем выигрыш и в чем проигрыш?
Дата добавления: 2015-02-09; просмотров: 286; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Примеры антивирусных приложений | | | Добавочно-дополняющая модель В. Хендерсон |