
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 2. Характеристики сигналов
Характеристики сигналов
Обобщенная структурная схема системы телекоммуникаций
Классификация преобразователей
Способы преобразования сообщения в сигнал и обратно
Преобразователи звук – сигнал
Преобразователи неподвижное изображение - сигнал
Преобразователи подвижное изображение - сигнал
Характеристики гармонического сигнала. Сигналы, которые мы используем в телекоммуникационных сетях, будь то аналоговые или цифровые, существуют в форме электрического напряжения и тока. Величина такого напряжения или тока изменяется с течением времени, и это изменение содержит информацию. Наиболее простым является сигнал, изменяющийся по закону косинуса и называемый косинусоидальным или гармоническим.
Мы можем рассматривать любой телекоммуникационный сигнал как комбинацию косинусоидальных колебаний с различными амплитудами и частотами. Частота определяется числом циклов или полных колебаний в секунду. Например, мы слышим колебания давления воздуха как звук. Мы в состоянии услышать частоты в диапазоне приблизительно от 20 Гц до 15 кГц, где 1 Гц (герц) представляет 1 цикл в секунду. Мы ощущаем эти колебания как звуки низких и высоких тонов.
Пример переменного напряжения гораздо важнее. Переменное напряжение периодически изменяет свои направление и величину,несколько десятков раз в секунду. Полное колебание напряжения известно как цикл, а частота колебаний напряжения определяется как число циклов в секунду. Если напряжение имеет 1 000 полных колебаний в секунду, то частота - 1 000 Гц или 1 кГц.
Рис. 4.3 показывает в виде стрелки рамку из провода, вращающуюся в постоянном магнитном поле. Магнитный поток, пронизывающий рамку, пропорционален синусу угла между плоскостью рамки и направлением магнитного поля. Поскольку магнитный поток меняется, то между концами рамки индуцируется напряжение, величина которого изменяется по закону косинуса во времени:
|
Здесь:
-(2  ft – φ) - фаза колебания в радианах.
ft – φ) - фаза колебания в радианах.
- f – частота, равная числу полных колебаний (циклов) в секунду, измеряется
в Гц. Она характеризует скорость протекания процесса.
- 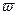 = 2
= 2  f – угловая частота, которая измеряется в радианах в секунду;
f – угловая частота, которая измеряется в радианах в секунду;
- t – время, измеряемое в секундах,
- φ – начальная фаза колебания в момент t = 0, она характеризует время задержки волны при прохождении через сеть. В самом деле, пусть на входе сети начальная фаза колебания равна нулю, а на выходе – φ. Выходное колебание тогда можно представить в виде:
|
где  играет роль времени задержки.
играет роль времени задержки.
Период Т представляет время одного цикла, т.е. время полного колебания:
T=1/f и f=1/T
Максимальная величина  колебания называется амплитудой. Квадрат этой величины служит энергетической характеристикой колебания.
колебания называется амплитудой. Квадрат этой величины служит энергетической характеристикой колебания.
Колебание, распространяющееся в пространстве, называется волной. Длина волны  представляет собой расстояние, на которое распространяется волна за 1 цикл или за 1 период:
представляет собой расстояние, на которое распространяется волна за 1 цикл или за 1 период:
 = c/f = cT,
= c/f = cT,
где c скорость распространения волны. Скорость распространения звуковой волны в воздухе равна примерно 346 м/с; для световых или радиоволн c = 300 000 км/сек.
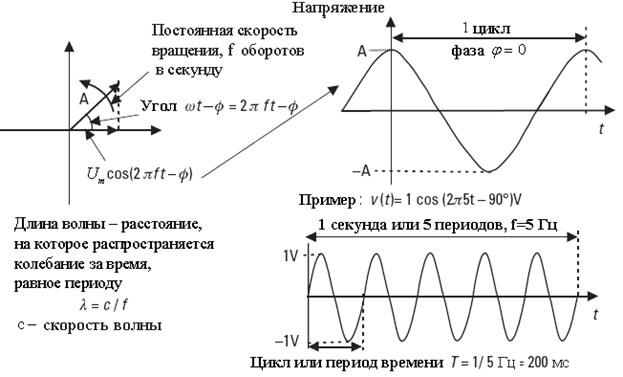
Рис .4.3 Косинусоидальное колебание и его параметры
Частотные диапазоны в телекоммуникациях. Информационный сигнал, как правило, является низкочастотным, но мы можем использовать для его транспортировки высокочастотный сигнал, называемый несущим колебанием. Для того нужно изменять амплитуду, частоту или начальную фазу несущего колебания по закону информационного сигнала. Такой процесс называется модуляцией. С помощью модуляции телекоммуникационные сигналы можно разместить в самых различных частотных диапазонах.
Рис.4.4 показывает частотные диапазоны, связанные с ними среды для распространения телекоммуникационных сигналов, способы их передачи и применения.
Скорость передачи определяется темпом, в котором цифровые сигналы передаются по сети. Обобщенно скорость передачи r измеряется в битах в секунду (бит/с).
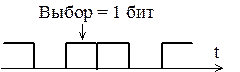
Бит - минимальное сообщение, означающее выбор одного из двух значений: "0" и "1". 8 бит составляют 1 байт, с помощью которого можно закодировать любое значение цифрового сигнала. На передачу через сеть сигнала со скоростью 2 бит/с обычно требуется 1 Гц полосы пропускания.
Спектр сигнала. Реальные сигналы электросвязи сложны, но любой из них можно представить совокупностью ряда гармонических составляющих (гармоник). Совокупность частот гармонических составляющих, соответствующих одному сигналу, принято называть спектромэтого сигнала. Разность между максимальной и минимальной частотами спектра называется шириной спектра (Гц) сигнала 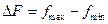 . Чем сильнее форма сигнала отличается от синусоиды, тем больше составляющих содержит сигнал и тем шире его спектр. Спектр сигнала - одна из самых важных особенностей аналоговых сигналов и это - также самый важный фактор, ограничивающий их скорость передачи.
. Чем сильнее форма сигнала отличается от синусоиды, тем больше составляющих содержит сигнал и тем шире его спектр. Спектр сигнала - одна из самых важных особенностей аналоговых сигналов и это - также самый важный фактор, ограничивающий их скорость передачи.
В технике телекоммуникаций спектр сигнала сокращают. Это связано с тем, что аппаратура имеет ограниченную полосу пропускания частот. Сокращение спектра осуществляют исходя из допустимых искажений сигнала. Например, при телефонной связи требуется, чтобы речь была разборчивой и абоненты могли узнавать друг друга по голосу. Для выполнения этих условий достаточно передать речевой сигнал в полосе частот от 300 до 3400 Гц. Ширина спектра телефонного сигнала зависит от скорости его передачи и обычно принимается равной F ≈ 1,5υ, где υ – скорость передачи (телеграфирования) в Бодах, т. е. в числе символов, передаваемых в секунду. Так, при телетайпной передаче υ = 50 Бод и F = 75 Гц.

Рис 4.4 Частотные диапазоны, используемые в телекоммуникациях
Единицы измерения параметров. В технике связи наряду с абсолютными единицами измерения параметров электрических сигналов (мощность, напряжение и ток) широко используются относительные единицы.
Уровнем передачи сигнала в некоторой точке канала или тракта называют логарифмическое преобразование отношения энергетического параметра S (мощности, напряжения или тока) к отсчетному значению этого же параметра. Правило преобразования определяется формулой:
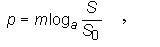
где m - масштабный коэффициент, a - основание логарифма, 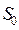 - эталонное значение параметра.
- эталонное значение параметра.
Уровни передачи измеряются в децибелах, если справедливы соотношения:

для уровней по мощности в дБм (децибелы по мощности);

для уровней по напряжению, дБн (децибелы по напряжению).
Уровень передачи называется абсолютным, если P0=1 мВт. Если теперь уровень задать на сопротивлении R0, то при заданных значениях мощности и сопротивления легко получить соответствующие величины напряжения U0 на сопротивлении:
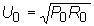
При R0= 600 Ом в практических расчетах принимают округленное значение U0= 0,775 В.
Усиление, ослабление и измерение мощности в децибелах. На длинном пути в телекоммуникационных сетях сигнал ослабляется и усиливается все снова и снова. Мощность сигнала жестко контролируют для того, чтобы она была достаточно высокой по отношению к шумам, и в то же время для того, чтобы она была достаточно низкой во избежание перегрузки сети и связанных с нею искажений сигнала. Когда уровень сигнала уменьшается, то это выражают с помощью термина «ослабление» по мощности. Когда сигнал восстанавливают, то это выражают с помощью термина «усиление» по мощности. Таким образом, ослаблению в 10 раз соответствует усиление в 10 раз.
Александр Белл первым предложил использовать логарифмическую шкалу для измерения уровня мощности. Шкала оказалась удачной, и это нашло свое выражение в том, что усиление мощности стали выражать в децибелах (дБ). Коэффициент усиления в децибелах определяется по формуле:
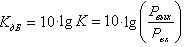
Если выходная мощность больше входной, то имеет место усиление и 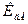 положителен, в противном случае он становится отрицательным. Если мощности выходного и входного сигналов одинаковы, то нет ни усиления, ни ослабления и
положителен, в противном случае он становится отрицательным. Если мощности выходного и входного сигналов одинаковы, то нет ни усиления, ни ослабления и 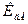 равен нулю.
равен нулю.
На рис. 4.4 представлен элемент телекоммуникационной сети с определенным входом и выходом. Приведенные формулы определяют усиление и ослабление мощности сигнала при передаче. В телекоммуникационной сети мы обычно имеем много (часто более 100) элементов, расположенных цепочкой.
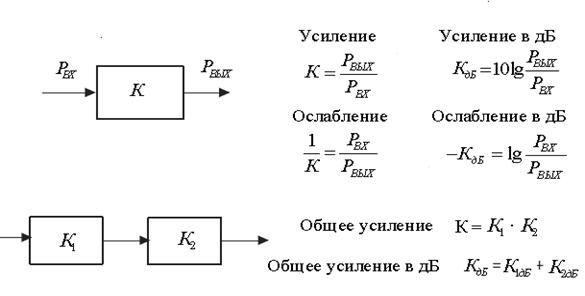
Рис. 4.4. Расчеты усиления и ослабления для участков сети
Если нужно вычислить общее усиление или ослабление, то нужно перемножить соответствующие коэффициенты отдельных элементов, Если же коэффициент каждого элемента представлен в децибелах, то они складываются, как показано на рисунке. Децибелы позволяют складывать малые положительные или отрицательные величины вместо того, чтобы их перемножать. Например, усилению в два раза соответствует (усиление) 3 дБ, усилению в 10 раз - 10 дБ и т.д.
Уровни мощности . Уровни мощности в телекоммуникационных сетях меняются в широких пределах , от пиковатт до десятков ватт, что соответствует вариации от 1 до 1 000 000 000. Измерение мощности, основанное на децибелах, позволяет легко выразить этот широкий диапазон мощностей. Абсолютный уровень мощности часто выражают в дБм0, сравнивая измеренную мощность с 1 мВт. Уровень мощности в дБм дается формулой:
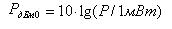
Если требуется определить мощность в милливаттах, то мы легко можем это сделать по известному значению p. Абсолютный уровень в дБм часто используется вместо выражения мощности в ваттах, например при определении входной мощности по известным величинам входной мощности и коэффициента усиления:

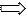
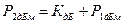
Примеры таких расчетов для радиолинии и участка волоконно-оптической связи приведены на рис. 4, 5
Рис. 4.5 Расчеты уровней выходной мощности для радиолинии и участка волоконно-оптической связи
Дата добавления: 2015-02-09; просмотров: 379; Мы поможем в написании вашей работы!; Нарушение авторских прав |
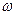 t - φ ) =
t - φ ) = 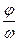 ) ,
) ,