Расчет обмотки

В статоре СГ применяем двухслойную петлевую обмотку. Использование таких обмоток позволяет уменьшить расход меди и изоляционных материалов, а также улучшить форму кривой ЭДС E₀.

Для определения числа витков в обмотке одной фазы статора определяем величину магнитного потока под полюсом в режиме холостого хода Φ_δ0 и ЭДС E₀

Φ_δ0 = B_δ0 l τ α_i , Вб 1.9

где α_i – коэффициент формы магнитной индукции по полюсом, равный 0,716.

E₀ = k_eU_ф, В 1.10

где U_Ф – номинальное фазное напряжение статорной обмотки СГ, равное

U_Ф = U_Н / В,

Приводим расчеты по формулам 1.9 … 1.10 и записываем полученные значения

Φ_δ0 = ____________ Вб, E₀ = ____________ В

Определяем предварительное число витков в одной фазе обмотки статора w_ф

1.11

Коэффициент k_b = k_ф – коэффициент формы поля

Приводим расчеты по формуле 1.11 и записываем полученное значение w_ф , округляя до целого четного числа. Принимаем w_ф = __________

Далее рассчитываем номинальный ток фазы, А,

1.12

Приводим расчет по 1.12 и записываем величину ___________А

Обмотка статора укладывается в пазы сердечника статора в два слоя, как принято выше. На рис.3 для примера приведен рисунок паза с уложенной в два слоя обмоткой и пазовой изоляцией.

Число пазов Z в сердечнике статора зависит от числа фаз обмотки и числа пар полюсов. Вычисляем число пазов Z сердечника статора, учитывая заданное число фаз обмотки m и полученное в 1.3. число пар полюсов р

Z = 2pmq 1.13

где q — число пазов приходящихся на полюс и фазу.

При числе полюсов 2p > 8 и малом полюсном делении число q выбирается дробным. При дробном q уменьшается отрицательное влияние высших гармоник ЭДС в статорной обмотке.

Принимаем для всех вариантов ,

Приводим расчеты по формуле 1.13 и записываем полученное значение Z = _______ .

Определяем число эффективных проводников в пазу N_П

1.14

где a — число параллельных ветвей обмотки фазы.

При выборе числа параллельных ветвей а , ток в одной параллельной ветви должен быть в пределах 50 … 150 А для применения стандартного обмоточного провода. В данном случае, при сравнительно небольшой мощности ( до 15,0 кВт ), для всех вариантов принимается a = 1.

Вычисляем N_n по 1.14. и принимаем целое число, рассматривая способ укладки проводников в пазу в два слоя.

При большом числе пар полюсов ( 2p > 8 ) проводники в пазу сердечника статора следует размещать так, чтобы высота паза была больше его ширины, так как при данном D и Z ширина паза не может быть большой. Например, при N_n = 8, по ширине можно расположить 2 проводника и по высоте 4, при этом в одном слое будет 4 проводников – 2 х 2. При N_n = 12, по ширине можно расположить 3 проводника, а по высоте 4, при этом в одном слое будет 6 проводников – 3 х 2. При N_n = 16 по ширине можно расположить 4 проводника, и по высоте 4, при этом в одном слое будет 8 проводников – 4 х 2.

Приводим расчет по 1.14 и записываем величину N_n = _____________ .

Уточняем число витков в фазе:

1.15

и окончательно записываем w_ф = _______________ витков

Определяем зубцовое деление t_z для сердечника статора – длину дуги по окружности диаметра D расточки статора, приходящуюся на один паз и один зуб – рис.4 .

Величина зубцового деления t_z, м равна , м 1.16

Уточняем линейную нагрузку, А/м,

1.17

Проводим вычисления и записываем t_z = ______________ м ( с точностью до десятых долей мм ) и величину А = _____________ А/м ( с точностью до десятых долей А/м ).

Определяем величину магнитного потока Ф _σ0 и магнитной индукции В_σ0 в режиме холостого хода:

1.18 1.19

Коэффициент k_b = k_ф – коэффициент формы поля

Приводим расчеты по формулам 1.18, 1.19 и записываем полученные значения

Φ_δ0 = _____________ Вб, B_δ0 = ____________Тл;

Определяем минимальную ширину зубца b_{Z min} . Эта величина ограничивается по двум параметрам.

Во-первых, по величине максимальной индукции в зубце B_Zmax. Как видно из рис.5, магнитная индукция в зубцах статора повышается по сравнению с магнитной индукцией в воздушном зазоре, поскольку примерно половина площади зубцового слоя занята пазами. Пазы, заполненные обмотками из меди и изоляцией, имеют большое сопротивление магнитному потоку, и магнитный поток вытесняется из пазов в зубцы.

		Рис.5 Участок магнитной цепи синхронного генератора 1 – лист сердечника статора, 2 – паз в листе сердечнике статора, 3 – зубец листа сердечника статора, 4 – полюс ротора Φδ0 - величина магнитного потока на холостом ходу

Для стали марки 1411, из которой обычно штампуются листы сердечника статора, допустимое значение индукции в зубце, B_Zmax = 1,6 … 1,9 Тл . Принимаем это значение и вычисляем минимальную ширина зубца b_{Z min} , м

,м 1.20

где k_c — коэффициент заполнения магнитопровода сталью, k_c = 0,95 при толщине листа Δ_л = 3,5·10^-4 м = 0,35 мм .

Величина b_{Z min} , во-вторых, ограничивается механической прочностью зубца. Из соображения механической прочности и технологичности при штамповке листов пакета статора целесообразно выбирать b _zmin 0,005 м. В противном случае следует увеличить диаметр расточки статора и повторить расчет.

Приводим расчеты по формуле 1.20 и записываем полученное значение b _zmin = _______________ м.

После определения b_{Z min} выполняется расчет паза сердечника ( рис.3, 4 ).

Для уменьшения сопротивления воздушного зазора и снижения зубцовых пульсаций пазы статора выполняют полуоткрытыми. При изготовлении обмотки статора из провода прямоугольного сечения (а х в) – рис.3, пазы оказываются прямоугольными, а зубцы — трапецеидальными – рис.4.

Определяем предварительное значение ширины паза b_П

, м 1.21

где h_k — высота коронки зубца ( рис.4 ), h_k составляет обычно (1,3 … 1,5)·10^-3 м.

Приводим расчеты по формуле 1.21 и записываем полученное значение

b_n = _____________ м.

Определяем сечение эффективного проводника обмотки статора - q _ЭФ мм²

1.22

где j₁ — допустимая плотность тока, А/мм²

Плотность тока в проводниках обмотки статора при продолжительном режиме работы зависит от условий охлаждения. При само вентиляции, согласно заданию, j₁ = (4,5 … 10)·10⁶ А/м² = 4, 5…12 А/мм².

Принимаем j₁ = 5 А/мм² , приводим расчеты по формуле 1.22 и записываем полученное значение

q _ЭФ = ________________ мм².

Полученное предварительно значение q _ЭФ может быть выполнено обычно применяемым обмоточным проводом типа ПНСДК и ПНСДКТ, имеющим минимальную толщину изоляции. Для принятого числа эффективных проводников в пазу N_n в одном слое обмотки будем располагать в пазу по его ширине, например, 3 проводника ( или 2 или 4 проводника ), а по высоте паза в одном слое 2 проводника. В этом случае в пазу окажется 12 ( или8 или 16 ) проводников обмотки.

Предполагая указанное расположение проводников, найдем допустимую в пазу ширину изолированного проводника a_изp , м

1.23

где n_ш — число эффективных проводников по ширине паза, равное 2 или 3 или 4;

Δn — толщина пазовой изоляции ( рис.3 ).

В качестве пазовой изоляции используют стеклослюдиниты и полиамидную пленку. В этом случае суммарная толщина изоляции на сторону Δn обычно составляет (0,18 … 0,22)·10^-3 м.

Приводим расчеты по формуле 1.23 и записываем полученное значение a_изp = _______________м.

Определяем расчетную допустимую ширину неизолированного провода a_неизp

a_неизp = a_изp – Δ_из, м 1.24

где Δ_из — толщина изоляции провода на обе стороны.

Для обмотки статора применяют провода с двухсторонней толщиной изоляции Δ_из = (0,2 .. 0,3)·10^-3 м.В данном случае приводим расчеты по формуле 1.24 и записываем полученное значение

a_неизp = _________________ м.

Принимаем стандартные размеры серийно выпускаемых неизолированных проводов типа ПНСДК и ПНСДКТ, близкие для полученного сечения q _ЭФ

a = 1,28 мм; b = 3,35 мм; q_a = 4,288 мм²;

a = 1,32 мм; b = 3,55 мм; q_a = 4,471 мм²;

a = 1,38 мм; b = 3,85 мм; q_a = 5,313 мм².

Прямоугольные проводники могут укладываться вертикально (рис а) или же плашмя (рис б).

После выбора провода уточняем ширину b_n и высоту паза h_n , а также фактическую плотность тока в обмотке.

Уточненная ширина паза составляет , мм,

b_n = n_ш(a + Δ_из) + 2 Δn, мм 1.25

Приводим расчеты по формуле 1.25, округляем в большую сторону до десятых долей мм и записываем полученное значение b_n = _________________ мм.

Определяем высоту h_n паза для двух слоев обмотки по 2 проводника в слое

h_n = n_b·(b + Δ_из) + 3·Δ_n + h_k + h_кл, мм 1.26

где n_b — число проводников по высоте паза;

h_кл — высота клина; принимаем высоту клина h_кл = (5 … 8)·10^-4 м,

h_k — высота коронки зубца ( рис.4 ), h_k составляет обычно (1,3 … 1,5)·10^-3 м.

Приводим расчеты по формуле 1.26 и записываем полученное значение h_n _______________ мм

Выполняем паз полуоткрытым и рассчитываем ширину щели полуоткрытого паза b_щ , чтобы можно было уложить провод обмотки

b_щ = a + Δ_из + Δ_щ, мм 1.27

где Δ_щ — припуск по ширине щели, принимается в пределах Δ_щ = (7 … 8)·10^-4 м.

Приводим расчеты по формуле 1.27 и записываем полученное значение b_щ = ___________ мм,

Для примера на рис. 6. приведен эскиз паза для N_n = 12 ( 3 х 2 х 2 слоя )

После расчета размеров паза, уточняем ряд предварительно принятых параметров.

Уточненная плотность тока j_a для выбранного сечения провода обмотки q_a

j_a = I_нф / q_a, А/мм² 1.28

Приводим расчет по 1.28 и записываем величину j_a = ____________ А/мм².

Уточняем минимальную ширину зубца

, м 1.29

Приводим расчет по 1.29 и записываем величину b _zmin = ___________ м

Уточненная индукция в узком сечении зубца

, Тл 1.30

Приводим расчет по 1.30 и записываем величину B_{Z MAX} = ________________ Тл.

Определяем высоту спинки статора h_a ( рис.4 )

м 1.31

где B_d — допустимая индукция в спинке якоря. Для стали 1411 B_d ≤ 1,5 Тл. Приводим расчет по 1.31 и записываем величину h_a = ____________, м

Определяем предварительно внешний диаметр статора D_а

D_а = D + 2h_n + 2h_a, , м. 1.32

Полученное значение D_а округляем до ближайшего нормализованного диаметра

( 0,52; 0,55; 0,60, 0,62; 0,65 ) и записываем величину наружного диаметра статора как D_н1 :

D_н1 = ________________ м.

Уточняем, если надо, высоту спинки статора h_a

,м 1.33

В случае отличия D_а и D_н1 приводим расчет по 1.33 и записываем величину h_a =______________, м

Уточняем индукцию в спинке статора B _d

, Тл 1.34

Приводим расчет по 1.34 и записываем величину B _d = ________________ Тл.

Рассчитываем шаг обмотки статора y₁ –частичный шаг обмотки одной фазы, равный числу пазов между двумя активными проводниками одной секции. Двухслойные обмотки статора, как правило, выполняют с укороченным шагом - y₁ = (0,8 … 0,86)τ_n,где τ_n = 3q₁._Величина _ q₁-число пазов на полюс и фазу, принята ранее 1, 1/4 = 1,25 ,

τ_n = 3 q₁ = 3. 1, 25 = 3,75 ___

тогда y₁ = 3,75 (0,8 … 0,86) = (3…3,225)

Приняв y₁ = __________ (целое число), определяем отношение β = y₁ / τ_n = 3/3,75 = 0,8 1.35

Рассчитываем параметры укладки секций обмотки статора - коэффициент укорочения k_у и коэффициент распределения k_p

1.36

Приводим расчет по 1.36 и записываем величину k_у = ___________

1.37

Известно, что q₁ = b + c / d, где b — целое число, c / d — правильная несократимая дробь, откуда bd + c = 1·4 +1 = 5, тогда k_{p = ____________________________}

Определяем для уточнения с ранее принятым значение обмоточный коэффициент k_о и приводим его величину

k_о = k_y·k_p = ______________ 1.38

Определяем коэффициент воздушного зазора kσ

1.39

где δ — величина воздушного зазора, принято в задании δ = 0,6 мм.

Определяем активное сопротивление одной фазы обмотки статора R_d , Ом .

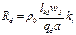1.40

где ρ₀ — удельное сопротивление меди при t = 20 °C, ρ₀ = 1,75·10^-8 Ом·м;
l_ср — средняя длина витка ;

k_t— температурный коэффициент сопротивления, k_t = 1,22.

a— число параллельных ветвей обмотки фазы, а = 1

Вычисляем среднюю длину витка секции обмотки l_ср

l_ср = 2 (l + l_л) , м 1.41

где l_л— длина лобовой части витка, равная

l_л = 1,4τ 1.42

Приводим расчет по 1.39 …1.41 и записываем величины

l_л = ______________ м, l_ср = _______________ м, R_d = _________________ Ом

Определяем индуктивное сопротивление рассеяния одной фазы обмотки статора - Хσ

, Ом 1.43

где λ_n, λ_д, λ_л — коэффициенты удельной проводимости пазового, дифференциального и лобового рассеяния, соответственно; μ₀ = 4π.10^-7 Гн / м, l= lσ.

Без расчета используем следующие значения:

Удельную проводимость пазового рассеяния для прямоугольного паза λ_n= 1,487

Удельную проводимость дифференциального рассеяния λ_д = 0, 142

Удельная проводимость лобового рассеяния λ_л = 0,278

Приводим расчет по 1.43 и записываем x_σ = _____________ Ом

Определяем индуктивные сопротивления одной фазы статорной обмотки ( синхронное сопротивление ) по продольной x_adи поперечной x_aq осям :

, Ом 1.44

, Ом 1.45

где Λ_ad, Λ_aq — коэффициенты проводимости машины по продольной и поперечной осям , соответственно.

Принимаем без расчета Λ_ad = 0,098; Λ_aq = 0,0958 и приводим расчеты по 1.44, 1.45. Записываем индуктивные сопротивления одной фазы статорной обмотки по продольной x_adи поперечной x_aqосям:

x_ad = ____________________Ом. x_aq = ________________________Ом.

Определяем полные индуктивные сопротивления одной фазы обмотки статора по продольной и поперечной осям, как сумму составляющей синхронного сопротивления и сопротивления рассеяния:

x_d = x_ad + x_σ , Ом 1.46

x_q = x_aq + x_σ; , Ом 1.47

Приводим расчет по 1.46, 1.47 и записываем

x_d = ______________________Ом;

x_q = _______________________Ом.

Определяем синхронное сопротивление одной фазы обмотки статора Х

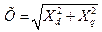1.48

Приводим расчет по 1.48 и записываем величину Х = _____________ Ом