Задачи для контрольной работы

Задача 1

Составить блок - схему алгоритма, написать программу на Паскале, вычислить значения переменных по заданным расчетным формулам и наборам данных:

№ варианта	Расчетные формулы	Данные
		a = 3.6 x = 0.7
		c = 2.4 x = -3.5
		b = 26.3 x = 2.5
		c = 16.7 x = 1.4
		c = 13.4 x = 1.5
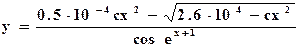
		c = 5.6 x = -2.4
		a = 0.6 x = 2.4
		a = 5.6 x = -1.2
		m = 2.1 c = -1.1 t = 1.5 b = 1.9
		a = 2.1 b = 0.02 x = 0.4
		c = 0.35 x = 1.44

Задача 2.

Составить программу, которая по заданным x и y определяет, принадлежит ли точка М(x, y) заштрихованной области.

Вариант 0	Вариант 1
y Вариант 2	Вариант 3
Вариант 4	Вариант 5
y Вариант 6	Вариант 7
Вариант 8	Вариант 9
x Вариант 10

Задача 3.

Даны натуральное число n и последовательность целых чисел а₁, а₂, ... , а_n. Составить блок-схему алгоритма, написать программу и провести вычисления в соответствии с заданием.

Вариант 0. Найти количество и сумму тех членов последовательности, которые делятся на 5 и не делятся на 3.

Вариант 1. Найти количество и удвоенную сумму всех положительных членов последовательности.

Вариант 2. Заменить все большие семи члены последовательности числом 7. Найти количество таких членов.

Вариант 3. Получить сумму отрицательных и количество положительных членов последовательности

Вариант 4. Все неотрицательные члены последовательности заменить на единицу. Найти количество и сумму отрицательных членов последовательности.

Вариант 5. Все члены последовательности, меньше двух, заменить нулями. Получить сумму и число членов последовательности, принадлежащих отрезку [3, 10].

Вариант 6. Все отрицательные члены последовательности уменьшить на 2, а все неотрицательные заменить на 1.

Вариант 7. Получить произведение членов последовательности, кратных шести. Найти количество таких членов.

Вариант 8. Найти количество членов последовательности, модуль которых при делении на 3 дает в остатке 1. Заменить эти элементы нулями.

Вариант 9. Определить количество и сумму членов последовательности, имеющих четные порядковые имена и являющихся нечетными числами.

Вариант 10. Определить количество тех членов последовательности, которые нечетны и отрицательны. Найти сумму членов последовательности, кратных 5.

Задача 4.

Дана действительная матрица А размера m x n. Составить блок-схему алгоритма, написать программу и провести вычисления в соответствии с заданием.

Вариант 0. Найти среднее арифметическое наибольшего и наименьшего элементов матрицы А.

Вариант 1. Провести нормирование элементов по строкам, разделив элементы i-ой строки (i =1, 2, ... , m) на , проводя анализ на возможность равенства нулю этой величины, не производя в этом случае нормирование.

Вариант 2. Найти сумму наибольших значений элементов строк матрицы А.

Вариант 3. Найти сумму элементов строки, в которой расположен элемент с наименьшим значением. Предполагается, что такой элемент единственный.

Вариант 4. Получить новую матрицу путем деления всех элементов матрицы А на ее наибольший по модулю элемент.

Вариант 5. Найти среднее арифметическое каждого из столбцов матрицы А.

Вариант 6. Найти среднее арифметическое каждого из столбцов, имеющих четные номера.

Вариант 7. Найти наименьшие значения элементов каждой строки матрицы А.

Вариант 8. Поменять местами строку, содержащую наибольший элемент, со строкой, содержащий наименьший элемент. Предполагается, что эти элементы единственны.

Вариант 9. Преобразовать элементы матрицы по правилу: отрицательные элементы заменить на –1, положительные – на 1, а нулевые оставить без изменения.

Вариант 10. Найти разности наибольших и наименьших элементов каждой строки матрицы А.

Задача 5.

Составить блок-схему решения задачи, написать программу с использованием подпрограммы (процедуры или функции) и провести расчет в соответствии с заданием.

Вариант 0. Даны действительные числа a, b, c. Получить

max(a² +b²).

Вариант 1. Даны действительные числа a, b. Получить

U = min (a, b), u = min (ab, a+b), min (u+u², p).

Вариант 2. Даны натуральные числа n, m и целые числа a₁, ... , a_n, b₁, ... , b_m. Получить

min (a₁, ... , a_n) + min (b₁, ... , b_m).

Вариант 3. Даны натуральные числа n, m и целые числа a₁, ... , a_n, b₁, ... , b_m. Получить

Вариант 4. Даны действительные числа s, t. Получить

f (t, -2s, 1,17) + f (2,2, t, s-t),

где

Вариант 5. Даны натуральные числа n, m и целые числа a₁, ... , a_n, b₁, ... , b_m. Получить

Вариант 6. Даны действительные числа a, b, c. Получить

.

Вариант 7. Даны действительные числа s, t. Получить

g (1,2, s) + g (t, s) – g (2s –1, st),

где

Вариант 8. Даны действительные числа x, y, z. Получить

f (xy, yz, x+y+z) + 2f (x-y, y-z, x-z),

где

Вариант 9. Даны действительные числа x, y. Получить

h (x, y) + h² (x-y), xy), h⁴ (x-y, x+y) + h (1, 1),

где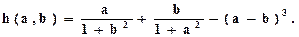

Вариант 10. Даны натуральные числа n, m и целые числа a₁, ... , a_n, b₁, ... , b_m. Получить

1+ (max (a₁, ... , a_n))² + (max (b₁, ... , b_m))².