ЛАБОРАТОРНАЯ РАБОТА № 11

ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ВОЗДУХА

ЦЕЛЬ РАБОТЫ: изучение основ молекулярно-кинетической теории газов и определение средней длины свободного пробега молекул воздуха.

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: делительная воронка, мерный стакан, секундомер, термометр, барометр.

I.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

Молекулярно- кинетическая теория строения вещества основана на трех положениях:

1. Все вещества состоят из отдельных частиц-молекул.

2. Между молекулами одновременно действуют силы взаимного притяжения и отталкивания.

3. Молекулы находятся в состоянии непрерывного беспорядочного движения.

В газах молекулы находятся на значительно большем расстоянии друг от друга, чем в жидкостях и твердых телах, и сила взаимного притяжения очень мала. Совершая хаотические движения, молекулы газа сталкиваются друг с другом, при этом изменяется их скорость движения, как по направлению, так и по величине.

Следует отметить, что молекулы сталкиваются друг с другом не соприкасаясь, т.к. уже при сближении в 10^-10м действуют значительные силы взаимного отталкивания.

То минимальное расстояние (между центрами молекул), на котором происходит столкновение, называется эффективным диаметром молекул. Путь, пройденный молекулой между двумя последовательными столкновениями, называется длиной свободного пробега молекул. Длина этого пути не одинакова, но благодаря большому числу молекул и беспорядочности их движения, можно говорить о средней длине свободного пробега молекул λ:

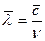
где 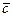-средняя скорость молекул,

u- число столкновений.

Средняя длина свободного пробега зависит от плотности, давления и температуры газа. С увеличением плотности и давления газа средняя длина свободного пробега уменьшится, а с повышением температуры она возрастет. Длина свободного пробега является важной характеристикой состояния газа.

В данной работе длина свободного пробега определяется из формулы, связывающей длину свободного пробега λ с коэффициентом внутреннего трения η :

где η -коэффициент внутреннего трения.

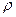-плотность газа,

-длина свободного пробега молекул,

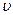-средняя арифметическая скорость молекул.

Из формулы (1) найдем:

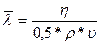
Плотность газа можно найти из уравнения Менделеева-Клапейрона

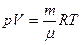
откуда

где p-давление газа,

-молярная масса,

R -универсальная газовая постоянная,

T -температура.

Средняя арифметическая скорость, согласно молекулярно-кинетической теории, равна:

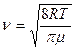(4)

Коэффициент внутреннего трения найдем из формулы Пуазейля:

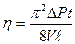(5)

где r – радиус трубки, по которой течет газ,

l – длина трубки,

V – объем протекшего газа,

t - время течения данного объема газа по трубке,

р – разность давлений на концах трубки.

Подставляя (3,4,5) в формулу (2) получим:

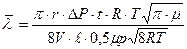(6)

После преобразований формула (6) примет вид:

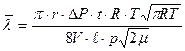(7)

Эта формула (7) и является расчетной для определения средней длины свободного пробега молекул газа.

II. ОПИСАНИЕ ЭКСПЕРИМЕНТА УСТАНОВКИ

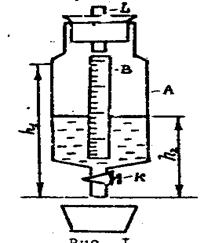
Рис.1

Лабораторная установка представляет собой делительную воронку А (рис.1), укрепленную на штативе. На воронку нанесена миллиметровая шкала В, на которой отмечается уровень воды в воронке. В воронку заливается дистиллированная вода на ¾ сосуда и закрывается пробкой, в которую вставлен капилляр L. Если открыть кран делительной воронки К, то вода будет выдавливаться под действием силы тяжести. Давление воздуха в сосуде станет меньше атмосферного и вода начнет вытекать не непрерывной струей, а отдельными порциями. Скорость вытекания воды сильно зависит от радиуса r. На концах капилляра создается разность давления р., численно равная гидростатическому давлению столба жидкости в воронке:

где 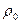- плотность воды, g – ускорение силы тяжести, h_ср – средний уровень воды в воронке.

Разность давления 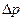будет заставлять воздух втекать в сосуд через капилляр. Через некоторый промежуток времени установится равномерное течение воздуха в капилляре, при котором объем воздуха, вошедшего через капилляр в воронку, будет равен объему вытекшей из воронки воды.

III. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Залейте в делительную воронку, дистиллированную воду и плотно закройте пробкой с капилляром.

2. Подставьте под кран воронки химический стакан. Откройте кран и, когда вода начнет вытекать отдельными порциями, подставьте мерный стакан. Отметьте уровень воды в воронке h₁ и включите секундомер.

3. Наберите в мерный стакан определенное количество воды (объем воды задается преподавателем), остановите секундомер и запишите время t, в течении которого вытекала вода, а, следовательно, и втекал воздух.

4. Отметьте уровень воды в воронке h₂ .

5. Вычислите разность давлений по формуле:

,

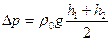принимая 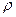₀ = 1000 г/м³, а g = 981 м/с².

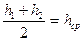( - есть средний уровень воды в воронке).

6. Снимите показания барометра и термометра, учитывая, что Т = t + 273 и

1 мм рт.ст. = 1333 дин/см².

7. Выпишите табличные данные для R = 8,31*10⁷ эрг/К моль

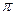= 3,14; m = 0,029 г/моль

8.Вычислите длину свободного пробега молекул воздуха по формуле (7)

9. Данные измерения занесите в таблицу 1 и 2.

Таблица 1

Постоянные величины

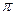
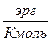
	m, г/моль	R,	r, см	l, см	V, см3	g, см/с2

Таблица 2

Результаты эксперимента

№:	h, cм	h2, см	р., дин/см2	t, с	Т,К	Р., дин/см2	, см
1. 2. 3.
Ср.

10. Сделайте выводы.

IV. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое скорость поступательного движения молекул газа?

2. Что принимается под средней длиной свободного пробега молекул? От каких характеристик состояния газа она зависит?

3. Объясните механизм взаимодействия молекул при столкновениях. Что называется эффективным диаметром молекул газа?