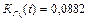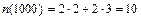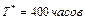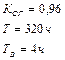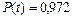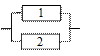КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
Зачет Д-410-3 Билет № 31
| № п/п
| Содержание вопроса
| |
| Какое из свойств, составляющих понятие надежности, можно использовать только для восстанавливаемых объектов?
Безотказность – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или некоторой наработки. Свойство безотказности проявляется как при использовании объекта по назначению, так и в периоды хранения и транспортирования.
Долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонта. Предельные состояния, как правило, указываются в технической документации.
Ремонтопригодность – свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов, повреждений, поддержанию и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонта.
Сохраняемость -свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности во время работы , а также после хранения и (или) транспортирования.
| |
| Пояснить сущность параллельного соединения элементов в смысле надежности. При таком соединении вероятность безотказной работы всей системы по отношению к вероятностям отказа каждого из элементов будет «больше большего» или «меньше меньшего»?

| Данная система работоспособна тогда, когда хотя бы один из ее n элементов работоспособен и неработоспособна (отказывает) в случае отказа всех ее n элементов. Тогда функция работоспособности будет описываться с помощью булевой алгебры следующим образом  . При замене булевого сложения (умножения) эквивалентными алгебраическими операциями функция работоспособности определяется как: . При замене булевого сложения (умножения) эквивалентными алгебраическими операциями функция работоспособности определяется как:  .
При этом: .
При этом:  
| | |
| Какой количественный показатель определяет математическое ожидание количества отказов объекта в единицу времени? Напишите для него статистическое выражение.
Это параметр потока отказов: 
| |
| Какие показатели надежности используются при задании требований по безотказности и ремонтопригодности к техническому объекту?
Наработкой на отказ Tн называется математическое ожидание времени работы между двумя соседними отказами восстанавливаемого объекта.
Для периода нормальной эксплуатации, на протяжении которого среднее число отказов в единицу времени неизменно  наработка на отказ является обратной величиной параметра потока отказов: наработка на отказ является обратной величиной параметра потока отказов:
 ,
Для простейшего потока отказов наработка на отказ численно совпадает со средней наработкой до первого отказа Tн = T *
Статистическое значение наработки на отказ Tн определяется как среднее арифметическое всех интервалов времени нормальной работы изделия в течение некоторого срока его эксплуатации. Если в течение этого срока было зафиксировано всего n отказов, а длительность интервалов работы между отказами была t1,t2 ,..,ti,..,tn, то ,
Для простейшего потока отказов наработка на отказ численно совпадает со средней наработкой до первого отказа Tн = T *
Статистическое значение наработки на отказ Tн определяется как среднее арифметическое всех интервалов времени нормальной работы изделия в течение некоторого срока его эксплуатации. Если в течение этого срока было зафиксировано всего n отказов, а длительность интервалов работы между отказами была t1,t2 ,..,ti,..,tn, то
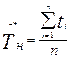 .
Наработка на отказ является удобным и важным показателем безотказности. Для аппаратуры военного назначения требуемое значение наработки на отказ включается в технические условия в качестве одного из основных показателей надежности. Для существующей техники связи и АСУ в зависимости от ее сложности наработка на отказ лежит в пределах нескольких тысяч часов.
Среднее время восстановления -именно этот показатель ремонтопригодностизадается в технических условиях на аппаратуру военного назначения.
Среднее время восстановления - это математическое ожидание времени восстановления работоспособного состояния объекта после отказа, TВ.
TB = .
Наработка на отказ является удобным и важным показателем безотказности. Для аппаратуры военного назначения требуемое значение наработки на отказ включается в технические условия в качестве одного из основных показателей надежности. Для существующей техники связи и АСУ в зависимости от ее сложности наработка на отказ лежит в пределах нескольких тысяч часов.
Среднее время восстановления -именно этот показатель ремонтопригодностизадается в технических условиях на аппаратуру военного назначения.
Среднее время восстановления - это математическое ожидание времени восстановления работоспособного состояния объекта после отказа, TВ.
TB =  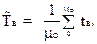 По соотношениям, аналогичным выражениям для средней наработки до отказа, можно показать, что при экспоненциальном распределении времени восстановления имеет место равенство
TB =
По соотношениям, аналогичным выражениям для средней наработки до отказа, можно показать, что при экспоненциальном распределении времени восстановления имеет место равенство
TB = 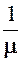 Среднее время восстановления включает затраты времени на отыскание неисправности и работу по ее устранению:
Тв = Тот + Ту
Для многих существующих типов аппаратуры связи и АСУ значения времени восстановления лежат в пределах от 20 до 100 минут, причем до 80% его приходится на Тот .
Среднее время восстановления включает затраты времени на отыскание неисправности и работу по ее устранению:
Тв = Тот + Ту
Для многих существующих типов аппаратуры связи и АСУ значения времени восстановления лежат в пределах от 20 до 100 минут, причем до 80% его приходится на Тот .
| |
| В чем ошибочно следующее утверждение: «С использованием каждого из известных показателей надежности можно количественно охарактеризовать только одно из свойств надежности восстанавливаемого объекта»?
В том, что можно охарактеризовать не только одно, но и несколько свойств надежности:
Ремонтопригодность – количественные показатели:  вероятность восстановления; вероятность восстановления;  интенсивность восстановления; интенсивность восстановления; 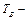 среднее время восстановления, а также их статистические показатели;
Безотказность – количественные показатели: среднее время восстановления, а также их статистические показатели;
Безотказность – количественные показатели:  параметр потока отказа; параметр потока отказа;  средняя наработка на отказ средняя наработка на отказ
| |
| Поясните сущность доверительной вероятности при экспериментальной оценке показателей надежности?
Доверительная вероятность – вероятность того, что показатель надежности попал в пределы доверительного интервала в результате эксперимента.
| |
| 
| Определить коэффициент готовности в момент времени t объекта, имеющего структурную схему надежности, представленную на рисунке, если КГ 1(t)=0,9; КГ 2(t)=0,8; КГ 3(t)=0,7; КП 4(t)=0,3.
| | |
| На испытания длительностью 1000 часов поставлено 4 однотипных восстанавливаемых объекта. За время испытаний у двух из них произошло по 2 отказа, а у остальных по 3. Каково значение средней наработки на отказ?
Ответ: 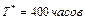
| |
| Определить вероятность безотказной работы системы за время t, если задан коэффициент оперативной готовности КОГ(t) = 0,96 и известно, что система имеет следующие показатели надежности Т = 320 ч., ТВ = 4 ч.
| |
| |
|


 наработка на отказ является обратной величиной параметра потока отказов:
наработка на отказ является обратной величиной параметра потока отказов:
 ,
Для простейшего потока отказов наработка на отказ численно совпадает со средней наработкой до первого отказа Tн = T *
Статистическое значение наработки на отказ Tн определяется как среднее арифметическое всех интервалов времени нормальной работы изделия в течение некоторого срока его эксплуатации. Если в течение этого срока было зафиксировано всего n отказов, а длительность интервалов работы между отказами была t1,t2 ,..,ti,..,tn, то
,
Для простейшего потока отказов наработка на отказ численно совпадает со средней наработкой до первого отказа Tн = T *
Статистическое значение наработки на отказ Tн определяется как среднее арифметическое всех интервалов времени нормальной работы изделия в течение некоторого срока его эксплуатации. Если в течение этого срока было зафиксировано всего n отказов, а длительность интервалов работы между отказами была t1,t2 ,..,ti,..,tn, то
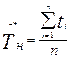 .
Наработка на отказ является удобным и важным показателем безотказности. Для аппаратуры военного назначения требуемое значение наработки на отказ включается в технические условия в качестве одного из основных показателей надежности. Для существующей техники связи и АСУ в зависимости от ее сложности наработка на отказ лежит в пределах нескольких тысяч часов.
Среднее время восстановления -именно этот показатель ремонтопригодностизадается в технических условиях на аппаратуру военного назначения.
Среднее время восстановления - это математическое ожидание времени восстановления работоспособного состояния объекта после отказа, TВ.
TB =
.
Наработка на отказ является удобным и важным показателем безотказности. Для аппаратуры военного назначения требуемое значение наработки на отказ включается в технические условия в качестве одного из основных показателей надежности. Для существующей техники связи и АСУ в зависимости от ее сложности наработка на отказ лежит в пределах нескольких тысяч часов.
Среднее время восстановления -именно этот показатель ремонтопригодностизадается в технических условиях на аппаратуру военного назначения.
Среднее время восстановления - это математическое ожидание времени восстановления работоспособного состояния объекта после отказа, TВ.
TB = 
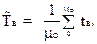 По соотношениям, аналогичным выражениям для средней наработки до отказа, можно показать, что при экспоненциальном распределении времени восстановления имеет место равенство
TB =
По соотношениям, аналогичным выражениям для средней наработки до отказа, можно показать, что при экспоненциальном распределении времени восстановления имеет место равенство
TB =  Среднее время восстановления включает затраты времени на отыскание неисправности и работу по ее устранению:
Тв = Тот + Ту
Для многих существующих типов аппаратуры связи и АСУ значения времени восстановления лежат в пределах от 20 до 100 минут, причем до 80% его приходится на Тот .
Среднее время восстановления включает затраты времени на отыскание неисправности и работу по ее устранению:
Тв = Тот + Ту
Для многих существующих типов аппаратуры связи и АСУ значения времени восстановления лежат в пределах от 20 до 100 минут, причем до 80% его приходится на Тот .
 вероятность восстановления;
вероятность восстановления;  интенсивность восстановления;
интенсивность восстановления;  среднее время восстановления, а также их статистические показатели;
Безотказность – количественные показатели:
среднее время восстановления, а также их статистические показатели;
Безотказность – количественные показатели:  параметр потока отказа;
параметр потока отказа;  средняя наработка на отказ
средняя наработка на отказ

 . При замене булевого сложения (умножения) эквивалентными алгебраическими операциями функция работоспособности определяется как:
. При замене булевого сложения (умножения) эквивалентными алгебраическими операциями функция работоспособности определяется как:  .
При этом:
.
При этом: