Теоретическое введение. Статистические методы прогнозирования являются одними из основных инструментов в деятельности плановых

Статистические методы прогнозирования являются одними из основных инструментов в деятельности плановых, аналитических, правительственных учреждений. В современных условиях существенно меняются информационные запросы управляющих структур по объему, составу, достоверности и оперативности производственных процессов. В связи с этим, для руководителей различных уровней возрастает роль прогнозов в принятии управленческих решений.

В данной работе делается статистический анализ и статистическое прогнозирование с целью повышения эффективности работы электрических схем.

Процесс анализа и прогнозирования включает следующие этапы:

- ввод данных в систему;

- визуализация данных с помощью различных типов графиков;

- преобразование данных, адекватное выбранным статистическим методам;

- реализацию алгоритмов статистических методов;

- вывод результатов анализа в виде графиков и таблиц с числовой и текстовой информацией;

- интерпретацию полученных результатов.

Основу исследования составляют временные ряды. Изучается вопрос изменения выходной мощности по мере изменения параметров элементов.

Вопрос изменения показателей может быть изучен с помощью специальных статистических методов, анализирующих ряды динамики.

Рядом динамики (временным рядом) называется последовательность значений статистического показателя, упорядоченная в хронологическом порядке. Отдельные наблюдения временного ряда называются уровнями ряда. В наших исследованиях применяются интервальные ряды с годовой динамикой развития. Уровни рядов динамики могут представлять абсолютные, относительные и средние значения. В данной работе используются средние оценки по предмету в группе.

Абсолютный прирост равен разности двух сравниваемых уровней. Он характеризует изменение показателя за определенный промежуток времени:

(1)

Для записи формулы базисного абсолютного прироста в общем виде уровень y_i сравнивают с показателем, принятым за базу:

(2)

Обобщающая характеристика скорости изменения исследуемого показателя во времени – это средний абсолютный прирост. Для его вычисления пользуются формулой:

(3)

Где - цепной абсолютный прирост,

n – длина временного ряда.

Еще одна характеристика динамики процесса – темп роста T. Она характеризует отношение двух сравниваемых значений ряда и выражается в процентах:

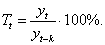(4)

Если измеряется цепной темп роста, то справедлива формула:

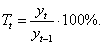(5)

Если измеряется базисный темп роста, то его вычисляют по формуле

(6)

Средний темп роста – обобщающая характеристика динамики процесса, отражающая интенсивность изменения уровней ряда. Он показывает сколько в среднем процентов последующий уровень составляет от предыдущего на всем периоде наблюдений. Этот показатель рассчитывается по формуле средней геометрической из цепных темпов роста:

(7)

Выразив цепные темпы роста через соответствующие уровни роста, получим

(8)

Темп прироста K характеризует абсолютный прирост в относительных величинах. Определенный в процентах темп прироста показывает на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения. Таким образом,

(9)

Преобразовав выражение (9), можно показать зависимость цепного темпа прироста от соответствующего темпо роста:

(10)

Для объективности анализа рассматривают абсолютное значение одного процента прироста, определяемое как отношение абсолютного прироста к соответствующему темпу прироста:

(11)

Наибольший интерес для статистического анализа представляет средний абсолютный прирост, средний темп роста, средний темп прироста, поскольку эти показатели являются обобщающими характеристиками динамики процесса. С их помощью были построены графики динамики ряда в виде прямой, которую можно продолжить на несколько шагов и получить прогноз развития процесса обучения. Для этого достаточно использовать формулу

Где L – период упреждения, y_n – фактическое значение в конечном уровне ряда, 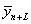- прогнозное значение (n + L) –го уровня ряда, - значение среднего абсолютного прироста рассчитанного временного ряда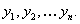

Очевидно, что такой подход к получению прогнозного значения корректен, если характер развития близок к линейному. К недостатку среднего прироста и среднего темпа роста следует отнести то, что они учитывают лишь начальный и конечный уровни временного ряда, исключая влияние промежуточных уровней. Тем не менее, этот метод дает в нашем случае хорошие результаты и может быть использован как приближенный, простейший способ прогнозирования, предшествующий более глубокому качественному анализу.