
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельного решения. 1. Кремер Н.Ш. и др. Высшая математика для экономистов / Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная
1. Кремер Н.Ш. и др. Высшая математика для экономистов / Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. – М. : Банки и биржи, 2000. – 439 с.
2. Шипачев В.С. Задачи по высшей математике: Учеб. пособие для вузов. – М. : Высшая школа, 2002. – 304с.: ил.
3. Сборник задач по высшей математике для экономистов: Учеб. пособие под ред В.И. Ермакова. – М. : Инфра,2006. – 516 с.
4. Малугин В.А Линейная алгебра: учеб пособие / В.А. Малугин. – М. : Рид Групп, 2011. – 464с. – (Национальное экономическое образование)
Дополнительная
5. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1»:Учеб пособие для вузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – 6-е изд. – М. : ООО «Издательство Оникс», ООО «Издательство «Мир и Образование», 2006. – 304с.: ил.
6. Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2»:Учеб пособие для вузов / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – 6-е изд. – М. : ООО «Издательство Оникс», ООО «Издательство «Мир и Образование», 2006. – 416с.: ил.
СПРАВОЧНЫЙ МАТЕРИАЛ
Тема: Матрицы и операции над ними
Матрицей размера (размерности) m´n называется прямоугольная таблица, содержащая m строк и n столбцов элементов.
Матрицы принято обозначать буквами: А, В, С,... (латинскими прописными), а элементы: аij, bij, cij,… (строчными с двойными индексами), где i – номер строки, j – номер столбца.
Например, матрица А размером m´n имеет вид

или, в сокращённой записи, А=(аij); i=1, 2, ..., m; j=1,2, ..., n.
Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т. е.  для любых i=1, 2, ..., m; j=1,2…, n.
для любых i=1, 2, ..., m; j=1,2…, n.
Далее будем рассматривать матрицы, элементами которых являются действительные числа.
Виды матриц
Например,
·  – матрица-строка,
– матрица-строка,
·  – матрица-столбец,
– матрица-столбец,
·  – квадратная матрица 2-го порядка,
– квадратная матрица 2-го порядка,
·  – диагональная матрица 3-го порядка,
– диагональная матрица 3-го порядка,
·  – единичная матрица 3-го порядка,
– единичная матрица 3-го порядка,
·  – нулевая или нуль-матрица
– нулевая или нуль-матрица
Матрица AT или A' называется транспонированной (обозначается сокращённо  , если элементы
, если элементы  связаны с элементами aij матрицы A соотношением
связаны с элементами aij матрицы A соотношением  .
.
Квадратную матрицу размера n´n называют матрицей n-го порядка.
Операции над матрицами
1. Транспонирование.
Например,  , тогда
, тогда  .
.
2. Умножение на скаляр (число).
Например,  , тогда
, тогда  .
.
3. Сложение и вычитание.
Например,  ,
,  , тогда
, тогда
 ,
,
 .
.
4. Умножение матриц.
Например,  ,
,  , тогда их произведением будет матрица размером 2´2 (обозначим её С), элементы которой вычисляются следующим образом:
, тогда их произведением будет матрица размером 2´2 (обозначим её С), элементы которой вычисляются следующим образом:
с11=1×0 + 2×2 + 1×1 = 5, с12=1×(–1) + 2×1 + 1×(–1) = 0,
с21 =3×0+ 1×2 + (–2)×1 = 0, с22=3×(–1) + 1×1 + (–2)×(–1) = 0.

Если исходные матрицы расположить следующим образом
 ,
,
то получится наглядная иллюстрация для выбора строки матрицы А и столбца матрицы В в расчёте элемента  матрицы С=A∙B: элемент
матрицы С=A∙B: элемент  стоит на пересечении соответствующей строки матрицы А и соответствующего столбца матрицы В.
стоит на пересечении соответствующей строки матрицы А и соответствующего столбца матрицы В.
5. Возведение в степень.
Например, 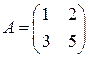 , тогда
, тогда  .
.
Две квадратные матрицы A и B называются перестановочными (коммутирующими), если AB=BA.
Тема: Определители и их свойства
Определителем (детерминантом) n-го порядка называется величина, характеризующая квадратную матрицу, вычисляемая по определённому правилу.
Для обозначения определителя матрицы А размером n´n.

используется символ  или det A или |A| или ∆.
или det A или |A| или ∆.
Правила вычисления определителей:
· определитель квадратной матрицы первого порядка равен её элементу, т. е.  ;
;
· определитель квадратной матрицы второго порядкаможно вычислить по формуле:
 ;
;
· определитель квадратной матрицы третьего порядкаможно вычислить по формуле:

Это правило называют правилом треугольников (см. [1, с. 17]);
Введём обозначение элементов определителя так: различными буквами обозначим различные строки, а различными индексами – различные номера столбцов. Тогда каждое слагаемое есть произведение элементов, взятых по одному из каждой строки и каждого столбца
 .
.
· определитель третьего порядкаможно вычислить также, например, разложением по первой строке:
 .
.
· определитель диагональной матрицы любого порядка равен произведению элементов главной диагонали.
Например,  .
.
· определитель квадратной матрицы любого порядка, приведённой к треугольному виду, равен произведению элементов главной диагонали.
Например, 
Матрица A–1 называется обратной матрицей для квадратной матрицы A, если A×A–1= A×A–1=E. Обратная матрица для матрицы A обозначается A–1.
Если |A|¹0, то матрица A имеет обратную A–1.
Если |A|=0, то матрица A обратной не имеет.
Минором  квадратной матрицы n-го порядка называется определитель (n–1)-го порядка, который получается из определителя исходной матрицы путём вычёркивания i-й строки и j-го столбца.
квадратной матрицы n-го порядка называется определитель (n–1)-го порядка, который получается из определителя исходной матрицы путём вычёркивания i-й строки и j-го столбца.
Алгебраическим дополнением Aij элемента aij матрицы называется число:
Aij = (–1)i+j× Mij.
Алгоритм вычисления обратной матрицы*
1. Найти определитель исходной матрицы А и сделать вывод о существовании обратной.
2. Транспонировать матрицу А.
3. Найти алгебраические дополнения элементов транспонированной матрицы и составить из них присоединённую матрицу 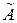 .
.
4. Вычислить обратную матрицу по формуле
 .
.
5. Сделать проверку A×A–1=A–1×A=E (можно устно).
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы и обозначается r(A) или rang(A).
Ранг квадратной матрицы А n-го порядка равен n (rang(A)=n), если det A¹0.
Для облегчения задачи определения ранга матрицы используются элементарные преобразования матрицы, не изменяющие её ранга, например:
· перестановка строк (столбцов);
· умножение строки (столбца) на число, отличное от нуля;
· сложение строки (столбца) с другой строкой (столбцом), умноженной на число.
Ранг матрицы равен числу линейно независимых строк этой матрицы. Число линейно независимых строк матрицы можно определить, подсчитав число оставшихся ненулевых строк в матрице, приведённой к ступенчатому виду. Например,
 .
.
Матричным называется уравнение, содержащее в качестве неизвестного матрицу. Простейшие матричные уравнения имеют вид:
1. AXB=C;
2. AX=B;
3. XA=B;
где A, B, C – известные матрицы, а X – неизвестная матрица соответствующих размеров.
Решением матричного уравнения является такая числовая матрица X, при подстановке которой в это уравнение получается верное матричное равенство.
Решения вышеприведенных уравнений находятся соответственно по формулам:
1. X=A–1CB–1, (при условии, что |A|¹0, |B|¹0)
2. X=A–1B, (при условии, что |A|¹0).
3. X=BA–1, (при условии, что |A|¹0).
Тема: Системы линейных алгебраических уравнений (СЛАУ)
Система из n линейных уравнений с n неизвестными 

может быть записана в матричном виде AХ=В, где
 – матрица-столбец неизвестных;
– матрица-столбец неизвестных;
 – матрица-столбец свободных членов;
– матрица-столбец свободных членов;
 – матрица коэффициентов системы, её определитель называется главным определителем системы;
– матрица коэффициентов системы, её определитель называется главным определителем системы;
 – расширенная матрица системы.
– расширенная матрица системы.
Система из n уравнений с n неизвестными (в этом случае матрица А – квадратная) имеет единственное решение в том и только в том случае, если главный определитель системы D=det A¹0.
Решение системы можно записать в виде  , где
, где  ,
, 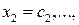
 .
.
Методы решения
1)  , i = 1,2,…, n (формулы Крамера),
, i = 1,2,…, n (формулы Крамера),
где Di – определитель матрицы, отличающейся от матрицы A тем, что в ней столбец с номером i заменён на столбец В;
2) X=A–1×B, где A–1 – матрица, обратная к A;
3) метод Гаусса или метод последовательного исключения неизвестных заключается в том, чтобы с помощью применения элементарных преобразований привести расширенную матрицу

(получается добавлением к матрице системы столбца свободных членов) к ступенчатому виду, например,
 ,
,
после чего осуществить обратный ход метода Гаусса (по матрице, приведённой к ступенчатому виду составить систему уравнений и решить её, начиная с уравнения, содержащего одно неизвестное).
Элементарные преобразования матрицы*:
1. Перестановка строк.
2. Умножение строки на число, отличное от нуля.
3. Сложение строки с другой строкой, умноженной на число.
Тема: Векторы
Вектор a, заданный в координатном пространстве Oxyz, может быть представлен в виде
a=axi+ayj+azk (разложение по осям координат, i, j, k – орты осей)

Координаты вектора a=(ax; ay; az).
Модуль вектора  .
.
Если даны векторы a=(ax; ay; az) и b=(bx; by; bz), то
· сумма векторов a+b=(ax+bx; ay+by; az+bz);
· разность векторов a–b=(ax–bx; ay–by; az–bz);
· произведение вектора на число: λa=(λax; λay; λaz), где λ – число.
Например, a=(3;–2;7) и b=(1;4;–6), тогда
 ;
;
 ;
;
 .
.
Если известны координаты точек – начала и конца вектора  :
:
А(xА , yА , zА), B(xВ, yB, zB), то его координаты можно найти по формуле:
 .
.
Тема: Скалярное произведение векторов и его свойства
Скалярное произведение векторов a и b – это число, равное произведению модулей векторов на косинус угла между ними:
 ,
,
где j – угол между векторами a и b.
Другие обозначения скалярного произведения: ab, (a, b).
При помощи скалярного произведения можно найти угол между векторами:
 .
.
Если векторы заданы координатами a=(ax; ay; az) и b=(bx; by; bz), то скалярное произведение векторов вычисляется по формуле:
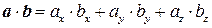 .
.
В некоторых приложениях употребляется n-мерная прямоугольная система координат, в которой формально введены не 2 или 3, а n взаимно перпендикулярных координатных осей. Вектор в такой системе – это набор из n упорядоченных чисел – координат конца вектора. Правила сложения, вычитания и вычисления скалярного произведения векторов такие же, как и для векторов в двух- или трёхмерном пространстве: если даны два вектора a= и b=
и b= , то их сумма (разность) имеют вид.
, то их сумма (разность) имеют вид.
a±b= 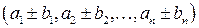 ,
,
а скалярное произведение
 .
.
Например, если в пространстве с n=5 заданы векторы a=(1, –1, 2, 0, –3) и b=(–1, 2, 0, 1, –1), то
a–b=(2, –3, 2, –1, –2),
ab= –1–2+0+0+3= 0 (равенство нулю скалярного произведения означает, что векторы перпендикулярны).
Задачи для самостоятельного решения
Условие каждой задачи выбирается индивидуально по последней и предпоследней цифрам номера студенческого билета или паспорта. Предпоследняя цифра в дальнейшем обозначается буквой M, последняя – буквой N. Например, для студенческого билета с номером № 247 вариант будет 47 и, соответственно, M=4, N=7(аналогично для паспорта). Для записи условия каждой задачи следует вместо букв M и N подставить соответственную цифру.
1. Вычислить выражение A2B–2B+CT, если  ,
,  ,
,  .
.
2. Определить ранг матрицы 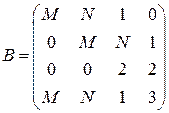 .
.
3. Даны матрицы A=(aij) и B=(bij) размерностью 3´3. Проверить, перестановочны ли матрицы A и B, и найти определители этих матриц. Элементы матриц вычисляются по формулам: aij= –i–j+M, bij= 2i–j+N–5.
4. Решить систему  .
.
а) методом Гаусса;
б) по формулам Крамера.
5. Даны точки A(M; N), B(N; M), C(M+1, N–5). Найти:
а)  – модуль вектора;
– модуль вектора;
б)  – скалярное произведение векторов;
– скалярное произведение векторов;
в) угол между векторами  и
и  .
.
6. Докажите, что векторы с и d перпендикулярны, если с = a–b, d = a+b, a=(М; –1; N; 0; –3) и b=(–1; 3; 0; M; N).
Задачи для подготовки (с примерным вариантом оформления)
(студенту, чей номер по списку группы совпадает с № 13, рекомендуется выполнить вариант № 31)
1. Даны следующие множества  ,
,  ,
,  .
.
Найдите: a)  ,b)
,b)  , c)
, c)  , d) B\A.
, d) B\A.
2. Найти области определения функций:
a)  ; b)
; b)  .
.
3. Найти пределы:
a)  ;
;
b)  ;
;
c)  ;
;
d)  ,
,
e)  .
.
4. Найти производные функций:
a)  ;
;
b)  ;
;
c)  .
.
5. Найти вторую производную функции  .
.
6. Исследовать функцию  и построить график.
и построить график.
7. Найти приближённое значение функции  в точке x=8+0,03 (1+M), используя понятие первого дифференциала.
в точке x=8+0,03 (1+M), используя понятие первого дифференциала.
8. Найти неопределённые интегралы:
Примерный вариант оформления задач
(студенту, чей № 13, рекомендуется выполнить вариант № 31)
вариант №13
1. Даны следующие множества  ,
,  ,
,  . Найдите: a)
. Найдите: a)  ,b)
,b)  , c)
, c)  , d) B\A.
, d) B\A.
Решение:
a) 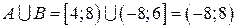 .
.
b)  .
.
c) 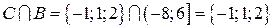 .
.
d)  .
.
Ответ: a)  ;
;
b) Æ;
c)  ;
;
d)  .
.
2. Найти области определения функций:
a)  ; b)
; b)  .
.
Решение:
a)  .
.
Функция определена, если дробь  неотрицательна и её знаменатель не равен нулю, поэтому областью определения данной функции является решение неравенства
неотрицательна и её знаменатель не равен нулю, поэтому областью определения данной функции является решение неравенства  . Методом интервалов определяем решение (рис.1):
. Методом интервалов определяем решение (рис.1): 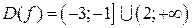 .
.

Рис.1
b)  .
.
Выражение, стоящее под знаком логарифма, должно быть положительным, а знаменатель дроби не должен равняться нулю, поэтому областью определения исходной функции является решение системы:
 или
или 
Тогда  .
.
Ответ: a) 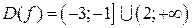 ,
,
b)  .
.
3. Найти пределы: a)  ; b)
; b) 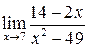 ; c)
; c)  ; d)
; d)  ; e)
; e) 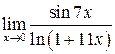 .
.
Решение:
a) Применяя теоремы о пределах, получим

b) Так как пределы числителя и знаменателя при  равны нулю, то имеет место неопределённость вида
равны нулю, то имеет место неопределённость вида  . После преобразования выражения, стоящего под знаком предела и сокращения подобных множителей неопределённость исчезнет.
. После преобразования выражения, стоящего под знаком предела и сокращения подобных множителей неопределённость исчезнет.
 ;
;
c) Числитель и знаменатель дроби  неограниченно возрастают при
неограниченно возрастают при  , поэтому имеет место неопределённость вида
, поэтому имеет место неопределённость вида  . Разделив числитель и знаменатель дроби на
. Разделив числитель и знаменатель дроби на 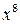 , получим:
, получим:
 ,
,
так как при  каждая из дробей
каждая из дробей  и
и  стремится к нулю.
стремится к нулю.
d)  .
.
Так как при  функция, стоящая под знаком предела, представляет собой степень, основание которой стремится к единице, а показатель к бесконечности, то имеет место неопределённость вида
функция, стоящая под знаком предела, представляет собой степень, основание которой стремится к единице, а показатель к бесконечности, то имеет место неопределённость вида  . Преобразуя функцию так, чтобы использовать второй замечательный предел, получим
. Преобразуя функцию так, чтобы использовать второй замечательный предел, получим
 .
.
Так как при  дробь
дробь  стремится к нулю, то
стремится к нулю, то
 ,
,
и, следовательно,  .
.
e) Заменив числитель и знаменатель дроби  эквивалентными бесконечно малыми функциями (
эквивалентными бесконечно малыми функциями (  ,
,  , при
, при  ), получим
), получим
 .
.
Ответ: a) 205; b)  ; c)1; d)
; c)1; d)  ; e)
; e)  .
.
4. Найти производные функций: a)  ;
;
b) 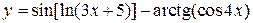 ; c)
; c)  .
.
Решение:
a)  .
.
 .
.
b) 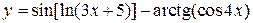 .
.
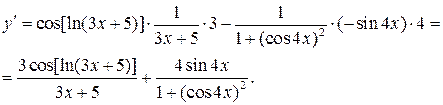
c)  .
.
Здесь основание и показатель степени зависят от x. Логарифмируя обе части равенства, получим  . Продифференцируем полученный результат по x. В нашем случае левая часть равенства
. Продифференцируем полученный результат по x. В нашем случае левая часть равенства  является сложной функцией, так как по условию
является сложной функцией, так как по условию  – это функция от x. Поэтому
– это функция от x. Поэтому  . Следовательно,
. Следовательно,
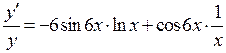 ,
,
откуда
 .
.
Ответ: a)  ;
;
b)  ; c)
; c)  .
.
5. Найти вторую производную функции  .
.
Решение:
 ,
,

 .
.
Ответ: 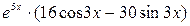 .
.
6. Исследовать функцию и построить график:  ; b)
; b)  .
.
Решение:
а)  .
.
Ø Область определения этой функции – вся числовая ось, за исключением точки x = 0, в которой функция имеет точку разрыва, т. е.
 .
.
Ø Первая производная функции  ,
,
 .
.
Ø Исследуем функцию на наличие экстремумов. Производная обращается в нуль при  и не существует при x = 0. Эти точки разбивают область определения на четыре интервала:
и не существует при x = 0. Эти точки разбивают область определения на четыре интервала:  ,
,  ,
, 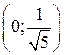 ,
,  , причём
, причём  в промежутках
в промежутках  ,
,  (функция возрастает) и
(функция возрастает) и 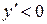 в промежутках
в промежутках  ,
, 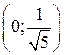 (функция убывает). Следовательно,
(функция убывает). Следовательно,  – точка максимума, а
– точка максимума, а  – точка минимума. Отметим, что
– точка минимума. Отметим, что  не принадлежит области определения функции и точкой экстремума быть не может.
не принадлежит области определения функции и точкой экстремума быть не может.
Ø Исследуем функцию на наличие точек перегиба. Вторая производная  не существует при
не существует при  . Эта точка разбивает область определения функции на два интервала:
. Эта точка разбивает область определения функции на два интервала:  ,
,  , причём
, причём  в промежутке
в промежутке  (график функции выпуклый вниз) и
(график функции выпуклый вниз) и  в промежутке
в промежутке  (график функции является выпуклым вверх). Отметим, что
(график функции является выпуклым вверх). Отметим, что  не принадлежит области определения функции и точкой перегиба быть не может.
не принадлежит области определения функции и точкой перегиба быть не может.
Ø Найдём асимптоты графика. Вертикальной асимптотой является прямая  , поскольку при приближении аргумента к нулю функция неограниченно возрастает (справа) или убывает (слева).
, поскольку при приближении аргумента к нулю функция неограниченно возрастает (справа) или убывает (слева).
Наклонные асимптоты – это прямые вида y = kx + b, где  ,
,  .
.
Замечание. Наклонную асимптоту также можно найти, преобразовав исходную функцию к виду  , где
, где 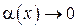 при
при  .
.
Преобразовав исходную функцию, получим
 ,
,
где  при
при  , следовательно, прямая y = 5x + 1 является наклонной асимптотой.[1]
, следовательно, прямая y = 5x + 1 является наклонной асимптотой.[1]
Так как предел  , то горизонтальных асимптот нет.
, то горизонтальных асимптот нет.
Ø Построим график функции, используя результаты, полученные при исследовании:

7. Найти приближенное значение функции 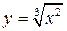 в точке x =8,06, используя понятие первого дифференциала.
в точке x =8,06, используя понятие первого дифференциала.
Решение:
Формула для вычисления приближенного значения функции, использующая понятие первого дифференциала имеет вид:
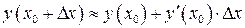 .
.
В нашем случае:
 ,
, 

 ,
,  ,
,  ,
,
 ,
, 
Ответ:  .
.
* Существуют и другие алгоритмы вычисления обратной матрицы. Приведён один из возможных.
* Преобразования аналогичны преобразованиям, применяемым для определения ранга матрицы, однако действия производятся исключительно со строками матрицы.
[1] Можно убедиться в правильности вычислений коэффициентов наклонной асимптоты, вычислив соответствующие пределы.
Дата добавления: 2015-02-10; просмотров: 299; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Обзор изменений законодательства в арбитражном процессе и в судебной системе за май-июль 2014 г. | | | ПОНЯТИЕ О МИКРОБАХ |