
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Измерение параметров непериодических процессов
Непериодический сигнал имеет сплошной спектр, т. е. полностью определяется комплексным параметром

измерение, которое производится теми же методами параллельного или последовательного спектрального анализа, которые были рассмотрены в предыдущем разделе. Так как интегрирование в бесконечных по времени пределах невозможно, удовлетворяются получением текущего спектра

который является функцией не только частоты, но и времени анализа Та . Точность измерения спектра тем выше, чем больше время анализа.
На практике часто ограничиваются определением ширины спектра, под которой понимают интервал частот, в котором сосредоточена основная часть энергии сигнала. Обычно это ширина главного лепестка. Во многих случаях бывает достаточно измерить еще более простые параметры сигнала.
Пример 54. В условиях, описанных в примере 34, измерен период колебании Т и логарифмический декремент затухания x Определить время установления показания.
 |
Решение. 1. Воспользуемся результатом, полученным в примере 38. Колебательный процесс будем считать закончившимся, когда его амплитуда достигнет 1 % от первоначального значения. На этом основании можно написать
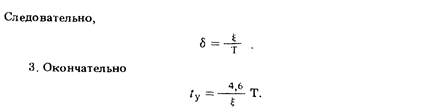
Большое практическое значение имеет измерение параметров импульсных процессов. Главными из них являются амплитуда, длительность, длительность фронта импульса. Основным средством измерений служит осциллограф, но при очень коротких импульсах возможности его ограничены. Поэтому применяются специфические методы и средства измерения параметров импульсов.
Метод измерения амплитуды, основанный на расширении импульса, заключается в том, что длительность импульса увеличивается до значения достаточного для измерения его амплитуды, например, вольтметром постоянного напряжения. При использовании цифровых приборов эта длительность составляет несколько миллисекунд. Функциональная схема расширителя импульса показана на рис. 104. Поступающим на его вход импульсом

конденсатор С заряжается до напряжения, близкого к Umах. После окончания импульса конденсатор медленно разряжается через сопротивление R. Коэффициент расширения импульса

обычно не превышает 103. Для получения большего коэффициента расширения применяют многокаскадные расширители, однако увеличивать число каскадов больше 2 ... 3 нецелесообразно, так как при этом ухудшается стабильность работы расширителя из-за влияния температуры на полупроводниковые приборы. При необходимости коэффициент расширения можно увеличить, применив схему ускорения заряда, а также отрицательную обратную связь, замедляющую разряд накопительного конденсатора.
Метод измерения амплитуды, основанный на амплитудно-временном преобразовании, состоит в том, что амплитуда импульса преобразуется в интервал времени, длительность которого, пропорциональная амплитуде, с большой точностью измеряется цифровым измерителем временного интервала. Структурная схема амплитудно-временного преобразователя изображена на рис. 105. За время действия входного импульса через диодное зарядное устройство конденсатор заряжается до напряжения, близкого к Umax . После окончания импульса он медленно разряжается через разрядное устройство, представляющее собой стабилизатор тока(см.рис.105,б).
Последний обеспечивает линейность разряда, вследствие чего интервал времени между двумя импульсами, вырабатываемыми устройством формирования интервала в начале. и в конце разряда (см. рис. 105, в) ,
T =  =kпUmax ,
=kпUmax ,


где v = const — скорость изменения напряжения на конденсаторе при разряде; kп — коэффициент преобразования. Метод измерения временных интервалов, основанный на счете импульсов, является наиболее распространенным из-за удобства ввода данных в ЭВМ и цифровые автоматы. Сущность его поясняется временными диаграммами, показанными на рис. 106. Старт-стопными импульсами, формируемыми в начале и в конце

измеряемого промежутка времени устройством формирования интервала (см. рис. 106, а), запускается и останавливается счетчик импульсов, вырабатываемых высокостабильным по частоте fкв кварцевым генератором (рис. 106, б). Через число сосчитанных импульсов N длительность измеряемого промежутка времени Т выражается следующим образом:
T=(N-1) Tи + Dt1 + Dt2
где Ти = 1/ fкв ~ период повторения импульсов, a Δt1и Δt2 — неизвестные интервалы времени между началом и концом измеряемого промежутка времени и, соответственно, первым и последним счетными импульсами. Неизвестное значение каждого интервала находится в пределах от О до Ти . Представим эту ситуацию математической моделью, показанной на рис. 107. Тогда числовые характеристики результата измерения будут:
_
T=NTи ;
иT = Tи / 
Точность измерения можно повысить за счет синхронизации, совместив со старт импульсом первый счетный импульс. Тогда

Такая точность приемлема, если Т >> Ти. При измерении длительности крутых фронтов и очень коротких импульсов используют стробоскопический и нониусный методы измерения временных интервалов.
Импульсные процессы могут иметь настолько сложную форму, что такие понятия, как амплитуда, длительность импульса и другие, становятся неопределенными. Что, например, можно сказать о параметрах импульса, показанного на рис. 108?

Для импульсных процессов сложной формы разработана система обобщенных параметров импульсов.
Под обобщенной амплитудой и длительностью импульса произвольной формы (без высокочастотного заполнения) понимаются амплитуда и длительность эквивалентного прямоугольного импульса, имеющего такую же площадь и энергию. Обобщенная амплитуда Um связана с максимальной амплитудой импульса Umax соотношением Um = Кф1 Umax, где Кф1— коэффициент формы, значения которого для импульсов наиболее распространенной формы приведены в табл. 24. Там же приведены выражения для обобщенных длительностей импульсов.
Обобщенная длительность фронта импульса произвольной формы (без высокочастотного заполнения) определяется как длительность фронта некоторого эквивалентного импульса с линейно нарастающим фронтом. При таком определении четко выражены начало и конец фронта, а скорость нарастания постоянна и равна отношению амплитуды к длительности фронта.
Понятия обобщенных мощности и длительности импульса с высокочастотным заполнением аналогичны. Ими целесообразно пользоваться во всех случаях, когда представляет интерес энергетическое воздействие импульса с высокочастотным заполнением.
Коэффициенты формы характеризуют отличие формы импульсов от прямоугольной. Чем больше их используется, тем полнее описание формы. Приборы, измеряющие обобщенные параметры импульсных процессов, называются интегральными измерителями параметров импульсов. Отечественной промышленностью они выпускаются в аналоговом и цифровом варианте.

5.3. ИЗМЕРЕНИЕ ПАРАМЕТРОВ СЛУЧАЙНЫХ ПРОЦЕССОВ
5.3.1. Измерение параметров стационарных случайных процессов
Процесс называется случайным, если при многократных повторениях он всякий раз протекает случайным образом.
Существуют два способа описания случайных процессов. При первом из них каждому текущему моменту времени t ставятся в соответствие случайные величины XiÎ{1,...,n} при втором — случайный процесс X(t) задается множеством своих реализации Xi(t) (рис. 109). Случайные величины Xi в каждом сечении t = const подчиняются определенному закону распределения вероятности. Если он одинаков для любого сечения, т. е. не зависит от времени, то процесс называется стационарным; в противном случае — нестационарным. Стационарные процессы обладают свойством эргодичности, заключающемся в том, что вероятностные характеристики, вычисленные по множеству реализации и по любой из них, равны между собой. Это позволяет при измерениях обходиться одной реализацией
 |
стационарного случайного процесса.
Исчерпывающая информация о случайном процессе содержится в его многомерной интегральной функции распределения вероятности
Fn(X1 , . . , Xn ; t1 , . . , tn ) = P{ X(t1) ≤ X1 , . . . ,X(tn) ≤ Xn},
характеризующей вероятность того, что в моменты времени ti случайные величины Xi, не превысят определенных своих значений, и в многомерной дифференциальной функции (плотности) распределения вероятности
pn (X1 , . . , Xn ; t1 , . . , tn )= 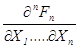
Применительно к одной реализации стационарного случайного процесса интегральная функция распределения вероятности F(X), определяемая как вероятность того, что значения X(t) лежат, ниже некоторого уровня Х (t) = Х = const (см. рис. 110), характеризуется относительным временем п  ребывания сигнала X(t) ниже этого уровня, т. е.
ребывания сигнала X(t) ниже этого уровня, т. е.
F(X) = P{ X(t) < X } = 
где Т — время измерения. На этом и основывается измерение F (X). Сигнал Х (t) подается на амплитудный селектор (см. рис. 111) с регулируемым порогом срабатывания Х ждущего одновибратора — триггера Шмитта, вырабатывающего прямоугольные импульсы единичной амплитуды (см. рис. 110), интегрирование которых позволяет найти оценку интегральной функции распределения вероятности по формуле ,

так как численное значение площади каждого i-го импульса равно его длительности tиi . Точность оценки тем выше, чем больше время измерения Т.

В дискретном варианте измерение функции распределения вероятности производится следующим образом. Стробирующее устройство (см. рис. 112, а) пропускает сигнал Х (t) только в моменты поступления на него импульсов опроса, вырабатываемых специальным генератором. В результате на амплитудный селектор поступают короткие импульсы, модулированные по амплитуде. Селектор представляет собой ограничитель, пропускающий только те импульсы, амплитуда которых больше порогового значения X. Число их подсчитывается счетчиком и позволяет получить оценку интегральной функции распределения вероятности по формуле

где n — показание счетчика; N — общее число импульсов опроса за время анализа Т. На рис. 112, б приведены временные диаграммы, иллюстрирующие измерение интегральной функции распределения вероятности стационарного случайного процесса этим методом.
 |
Плотность распределения вероятности стационарного случайного процесса,представленного одной реализацией, может быть выражена через относительное время пребывания сигнала Х [t) в интервале значений Х + ΔХ:

где обозначения ясны из рис. 113, а. Отсюда вытекает способ получения оценки плотности распределения вероятности

где tиi = Dtj могут рассматриваться как временные интервалы между фронтами импульсов, формируемых на время превышения сигналом X(t) уровней Х = const (см. рис. 113,6) и Х + DХ = const (рис. 113, в). Соответствующая структурная схема показана на рис. 114. Измеритель плотности распределения вероятности стационарного случайного процесса состоит из двух идентичных каналов, в которых вырабатываются прямоугольные импульсы единичной амплитуды, длительности которых в каждом канале равны, соответственно, времени превышения сигналом уровней Х и Х + DХ . Последние задаются регулятором уровней, обеспечивающим в то же время DХ = const. В устройстве вычитания формируются импульсы с единичной амплитудой и длительностью tиi (см. рис. 113, г), интегрирование которых позволяет получить в отсчетом устройстве оценку 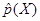 . Точность оценки тем выше, чем меньше DХ и чем больше время измерения Т.
. Точность оценки тем выше, чем меньше DХ и чем больше время измерения Т.
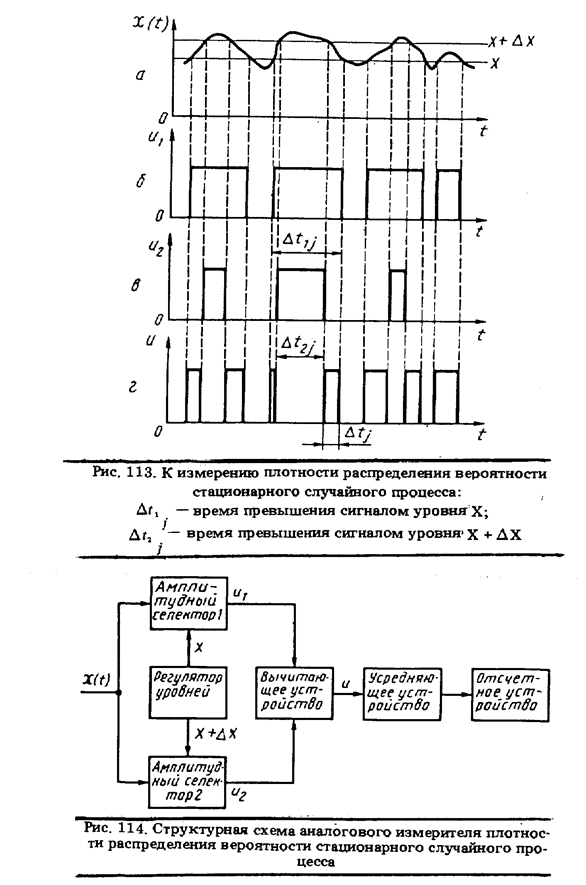 При дискретном измерении плотности распределения вероятности стационарного случайного процесса подсчитывается разность между количеством импульсов опроса, поступивших из двух идентичных каналов с разными пороговыми уровнями. Подробно работу измерителя можно проанализировать по рис. 115. Оценка плотности распределения вероятности получается по формуле
При дискретном измерении плотности распределения вероятности стационарного случайного процесса подсчитывается разность между количеством импульсов опроса, поступивших из двух идентичных каналов с разными пороговыми уровнями. Подробно работу измерителя можно проанализировать по рис. 115. Оценка плотности распределения вероятности получается по формуле
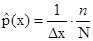
где по-прежнему n — показание счетчика, а N — общее число импульсов опроса за время анализа Т.

На практике часто ограничиваются измерением более простых параметров — моментов или числовых характеристик законов распределения вероятности стационарных случайных процессов.
Первый начальный момент (среднее значение или математическое ожидание стационарного случайного процесса)

представляет собой постоянную составляющую сигнала (см. рис. 116). Получение оценки среднего значения

сводится к усреднению сигнала за время измерения Т. Оно выполняется 'всевозможными фильтрами нижних частот (например, интегрирующими RC-цепочками или интегрирующими звеньями, построенными на основе использования усилителей постоянного тока с глубокой отрицательной обратной связью), магнитоэлектрическими механизмами, инерционными системами, устройствами с демпфированием и т. п. В цифровом варианте оценка среднего значения получается путем усреднения не самого сигнала, а его дискретных значений

где t — интервал между выборками из реализации Х (t), а п — число выборок.
Второй начальный момент (средняя мощность стационарного случайного процесса)

характеризует энергетический уровень сигнала. Для получения оценки

обычно используется квадратичное детектирование сигнала с последующим усреднением за время измерения Т. Среднее значение выходного напряжения после квадратичного Преобразователя можно измерять магнитоэлектрическим прибором. Проще всего задача измерения  решается с помощью вольтметров среднеквадратического значения, имеющих открытый вход. Показание такого вольтметра равно
решается с помощью вольтметров среднеквадратического значения, имеющих открытый вход. Показание такого вольтметра равно 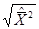 и не зависит от формы измеряемого напряжения.
и не зависит от формы измеряемого напряжения.
Второй центральный момент (дисперсия стационарного случайного процесса)

характеризует среднюю мощность переменной составляющей (флюктуаций) сигнала. Для получения ее оценки

также может быть использован вольтметр среднеквадратического значения, но с закрытым входом. Показания такого вольтметра будут соответствовать стандартному отклонению

Можно также воспользоваться соотношением

в котором оценка средней мощности, измеряемая цифровым прибором,
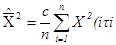
где с = const.
Мерой неопределенностизначений стационарного случайного процесса служит энтропия, для оценки которой

Используются l дискретных значений плотности распределения вероятности.
Мерой статистической связи между значениями стационарного случайного процесса без постоянной составляющей в моменты времени t1 и t2= t1 -t служит смешанный центральный момент 2-го порядка 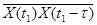 , называемый корреляционным. Вероятностно-статистические характеристики стационарного случайного процесса не зависят
, называемый корреляционным. Вероятностно-статистические характеристики стационарного случайного процесса не зависят
от времени, поэтому t1 можно выбрать произвольно; приняв t1= t. Тогда корреляционный момент будет зависеть только от τ:
 (29)
(29)
С переходом от фиксированного времени к текущему корреляционный момент стал функцией.
Определенная выражением (29) корреляционная функция обладает следующими свойствами.
1. При t= 0 корреляционная функция р(0)=Х(t)X(t)= Х2 =  максимальна и равна дисперсии стационарного случайного процесса (рис. 117). Если измеряемой физической величиной является, например, сила тока i(t), то r (0) =
максимальна и равна дисперсии стационарного случайного процесса (рис. 117). Если измеряемой физической величиной является, например, сила тока i(t), то r (0) = 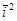 — полная мощность, выделяемая на сопротивлении в 1 Ом. В том случае, когда процесс имеет постоянную и переменную составляющие, r(0) =
— полная мощность, выделяемая на сопротивлении в 1 Ом. В том случае, когда процесс имеет постоянную и переменную составляющие, r(0) =  +
+  где
где  и
и  мощности, соответственно переменной и постоянной составляющих.
мощности, соответственно переменной и постоянной составляющих.

Максимальное значение корреляционной функции при t = 0 объясняется тем, что статистическая связь между неразличимыми по времени значениями X(t) является наибольшей.
Корреляционную функцию часто нормируют по ее максимальному значению: r (τ) = r (τ) / r (0). Тогда r (0) = 1.
2. Корреляционная функция является четной, т. е. р (τ) = r (—τ). Это можно показать, выбрав в качестве текущего момент времени t2 = t и обозначив t1= t2 + τ (см. рис. 116). Спектр корреляционной функции состоит, следовательно, только из косинусоидальных составляющих.
3. При τ→∞ r (τ) → 0 (у процессов с постоянной составляющей — к  ), если в X(t) нет детерминированной составляющих.
), если в X(t) нет детерминированной составляющих.
4. Корреляционная функция r(τ) монохроматического колебания являетсякосинусоидой с такой же частотой. Доказательство этого важного свойства приведено в примере 55, а важным следствием является то, что при корреляционном преобразовании теряется информация о фазовой структуре процесса.
5. Корреляционная функция суммы независимых процессов равна сумме их корреляционных функций. Вместе с предыдущим это свойство используется в оптимальной фильтрации для суммирования гармоник сигнала в момент τ= 0.
6. Корреляционная функция связана со спектральной плотностью мощности случайного процесса прямым и обратным преобразованиями Фурье:

которые с учетом четности корреляционной функции могут быть переписаны в виде:

Это положение известно как теорема преобразования Винера-Хинчина. Таким образом, энергетический спектр G(ω), как и корреляционная функция р (τ ), может служить неслучайной характеристикой случайного процесса.
На практике из-за конечности времени усреднения Т определяется не сама корреляционная функция, а ее оценка

что учитывается иногда внесением в результат измерения поправки. Представление о ней можно получить из следующего примера.
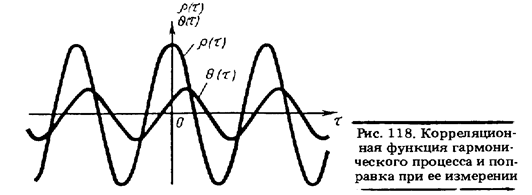
Пример 55.Найти корреляционную функцию гармонического колебания Х (t) = Xmax. sin (ωt + φ) и поправку при ее измерении с интервалом усреднения Т.
 Решение.Оценка корреляционной функции
Решение.Оценка корреляционной функции

Таким образом, поправка Θ (τ ) является гармонической функцией той же частоты, что и р (τ), но с начальной фазой, содержащей информацию о фазе гармонического колебания X(f) (рис. 118). Поправка Θ (τ ) особенно значительна на низких частотах и убывает с
увеличением времени усреднения Т. При τ → 0 корреляционная функция сложного сигнала р(τ) → р(0), так как поправки суммируются с разными фазами (в том числе и с противоположными).Средства измерений, предназначенные для определения корреляционной функции, называются коррелометрами. Различают коррелометры последовательного и параллельного действия. Структурная схема простейшего коррелометра последовательного действия приведена на рис. 119. Значения корреляционной функции получают, изменяя время задержки сигнала t. В многоканальном коррелометре параллельного действия осуществляется одновременное вычисление значений корреляционной функции при различных значениях t, тем самым сокращается время измерения. Упрощенная структурная схема такого коррелометра показана на рис. 120.
В цифровых коррелометрах все операции производятся с дискретными значениями сигнала. Современные цифровые анализаторы статистических характеристик являются, как правило, многофункциональными приборами, позволяющими измерять все основные параметры стационарных случайных процессов. В их число входит и энергетический спектр G(ω) , для определения которого цифровой коррелометр дополняется вычислительным устройством, осуществляющим быстрое преобразование Фурье. Энергетический спектр G(ω), представляющий собой спектральную плотность мощности (среднюю мощность сигнала, приходящуюся на единицу полосы частот), может измеряться и непосредственно спектроанализатором, к выходу которого подключается вольтметр среднеквадратического
значения с закрытым входом. В этом случае оценка энергетического спектра
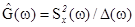
 где
где  — оценка средней мощности, выделяемой на сопротивлении 1 Ом спектральной составляющей сигнала с частотой ω, соответствующей средней частоте узкополосного фильтра с шириной полосы пропускания Δω. Эквивалентная структурная схема измерения показана на рис. 121. От спектрального анализа детерминированных процессов, являющегося линейным преобразованием, она отличается наличием квадратичного преобразования и усреднения.
— оценка средней мощности, выделяемой на сопротивлении 1 Ом спектральной составляющей сигнала с частотой ω, соответствующей средней частоте узкополосного фильтра с шириной полосы пропускания Δω. Эквивалентная структурная схема измерения показана на рис. 121. От спектрального анализа детерминированных процессов, являющегося линейным преобразованием, она отличается наличием квадратичного преобразования и усреднения.
 |
Дата добавления: 2015-02-10; просмотров: 263; Мы поможем в написании вашей работы!; Нарушение авторских прав |