Из теории изгиба известна зависимость кривизны балки следующего вида

С другой стороны из курса высшей математики кривизна плоской кривой может быть представлена через её координаты следующим образом:

Приравнивая (18.3) и (18.4) получим точное ДУУЛБ

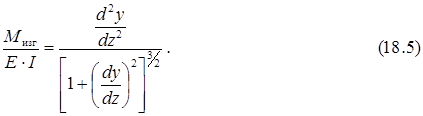
Полученное дифференциальное уравнение имеет большие трудности при решении, поэтому его упрощают, учитывая известную гипотезу малости деформаций

Учитывая небольшие углы поворота сечений для реальных балок получаем следующее приближенное ДУУЛБ, которое будет называться в дальнейшем основным дифференциальным уравнением упругой линии балки.

Данное уравнение справедливо для правой системы координат.

Полученное уравнение решается путем двойного интегрирования

В этом решении произвольные постоянные интегрирования представляют собой по геометрическому смыслу соответственно угол поворота и прогиб в начале координат

Произвольные постоянные интегрирования определяются из граничных или начальных условий построения расчетной схемы балки. Рассмотрим основные разновидности граничных условий.