Индивидуальное домашнее задание № 6 по теме

«Функции нескольких переменных»

Задание 1. Найдите область определения указанных функций:

1.1	z = ln((x + 1)(y - 2))
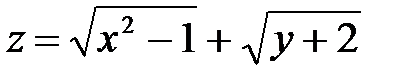
1.2	z = ln(y - x)	z = arccos(2y - x)
1.3
1.4		z = arcsin(x - 2y)
1.5
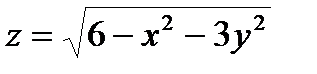
1.6	z = ln(3 + x - y²)	z = arccos(x + 3y)
1.7		z = x lnxy
1.8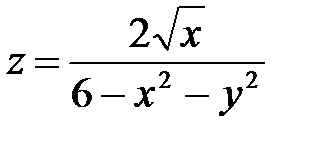
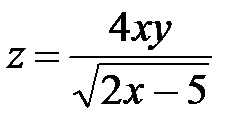
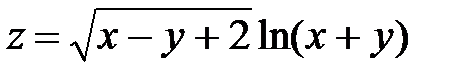
1.9		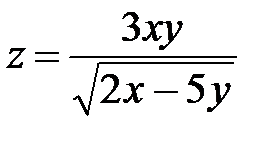z = ln(x² + y² - 3)
1.10	z = ln(4 - x² - y²)
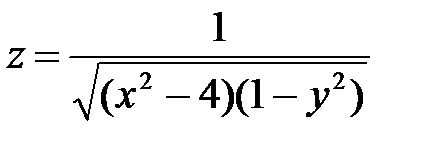
1.11	z = ln(4x² - y²)
1.12			z = ln(4x - y2- 8)
1.13
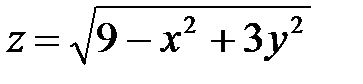
1.14
1.15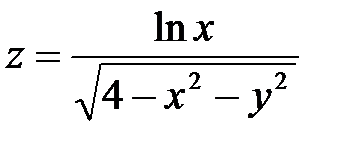
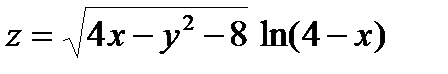
1.16

1.17
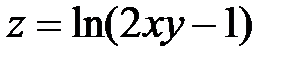
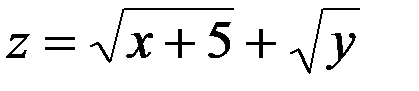
1.18			z = ln(y² + 8 - 4x)
1.19
1.20		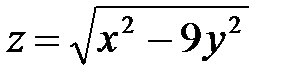z = ln(5 - xy)
1.21	z = arcsin(3y - 2x)	z = ln(y² - x² - 4)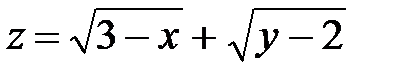
1.22
1.23	z = x lnxy	z = arccos(x² - y)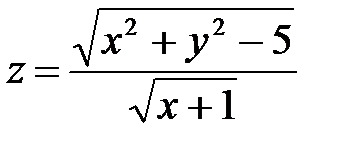
1.24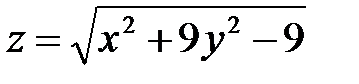
1.25	z = ln(4 - xy)	z = arcsin(2x - y²)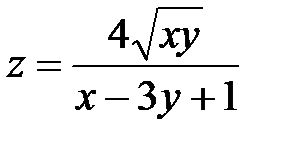
1.26			z = ln(2x² - y²)
1.27			z = arcsin(x² + y - 2)
1.28
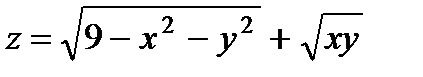
1.29
1.30			z = lg(4x²-9y²-36)

Задание 2. Вычислите значения частных производных , ,

для данных функций в точке :

2.1
2.2
2.3
2.4
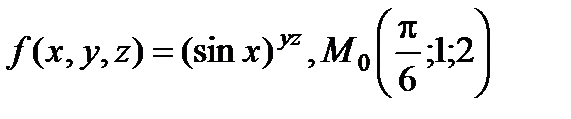
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12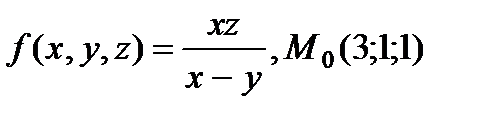
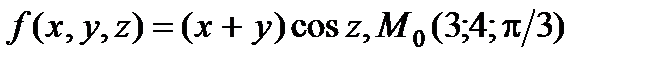
2.13
2.14
2.15
2.16
2.17
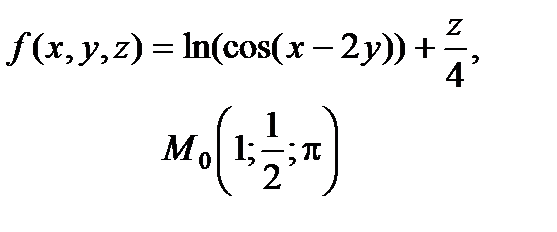
2.18
2.19
2.20
2.21
2.22
2.23
2.24
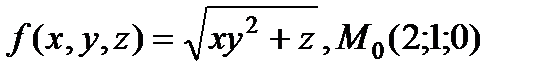
2.25
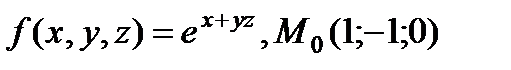
2.26
2.27
2.28
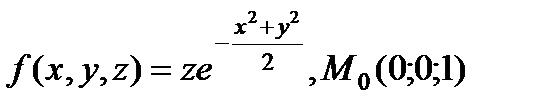
2.29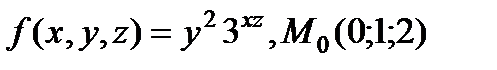
2.30

Задание 3. Найдите полные дифференциалы указанных функций:

3.1		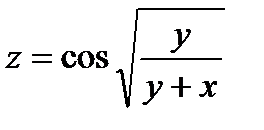z = arcsin(x² + xy)
3.2			z = xy³ + 1 - 3x²y
3.3	z = (2sinx + tgy)³	z = arctg(x - y)
3.4	z = x²y sinx - 3y
3.5
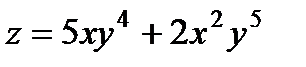
3.6	z = ln(x + xy - y²)		z = x sinxy
3.7	z = cos²(x² - y²) + x³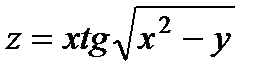
3.8
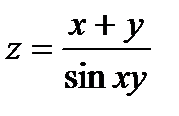
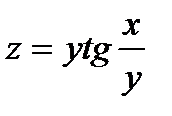
3.9	z = 2x³y - 4xy²		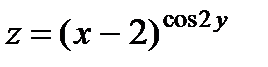z = arcctg(y² - 2x)
3.10	z = arcsinxy - 3xy	z = (1 - x²) ln(1 - 2xy)
3.11	z = ln(y² - x² + 3)		z = arccos(x - y)
3.12			z = 4 - x³ - y³ - 5y
3.13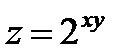
3.14	z = x ln(2x - 3y)
3.15			z = arctgex+2y
3.16		z = 3x²y² - 7xy³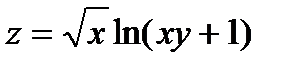
3.17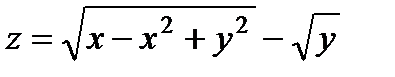
3.18		z = cos(3x + y) - x²	z = xy tg(x + y)
3.19	z =3x3y - arccosxy	z = (y² - 2) ln(3xy + 1)
3.20			z = arctg(2x - y)
3.21
3.22			z = sin²(4xy + y²)
3.23	z = sin²(y² - x²) + y4	z = ln(3x² - 2y³)	z =y ctg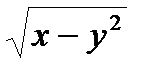
3.24
3.25
3.26
3.27	z = sin5(2xy - 1)	z = (y² - 1) lnxy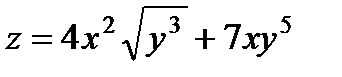
3.28
3.29
3.30

Задание 4. Найдите частные производные данных функций по независимым переменным:

4.1
4.2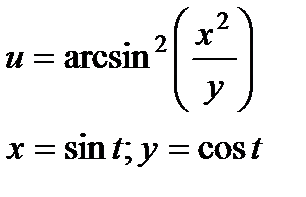
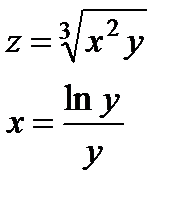
4.3
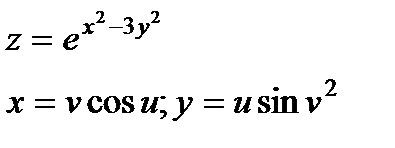
4.4
4.5
4.6
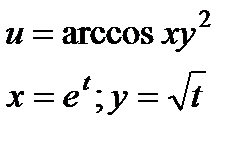
4.7
4.8
4.9
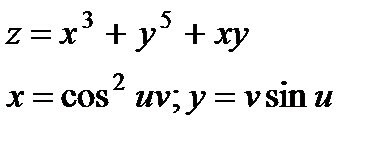
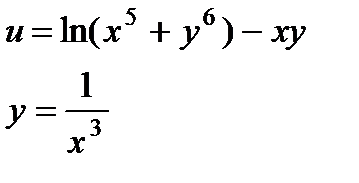
4.10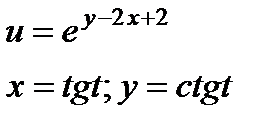
4.11
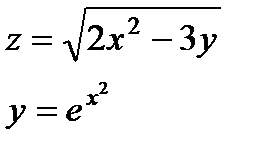
4.12
4.13
4.14
4.15
4.16
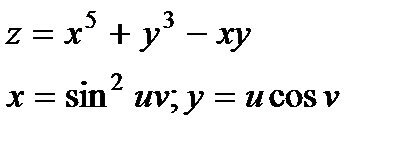
4.17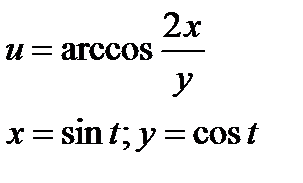
4.18
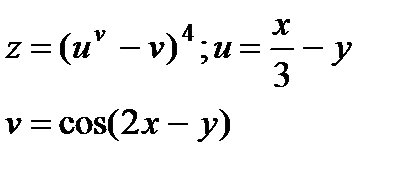
4.19
4.20
4.21
4.22
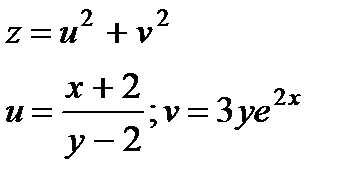
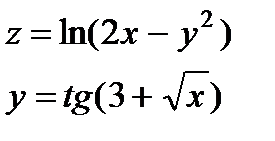
4.23
4.24
4.25
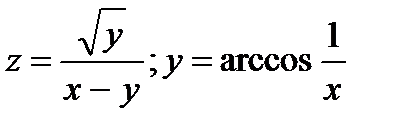
4.26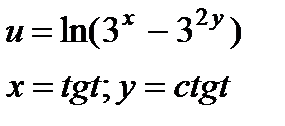
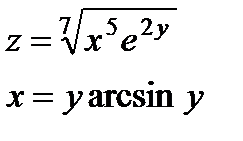
4.27
4.28
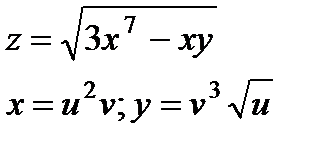
4.29
4.30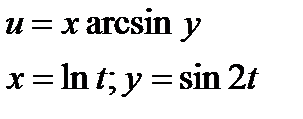

Задание 5. Найдите частные производные функции z , заданной неявно:

5.1		x² + y² + z² = y - z - 5
5.2		x cosz + z siny + tgz = 5
5.3	x² - y² - z² + 6z + 2x - 4y = 0
5.4	x² + y² + z² = xy + 2
5.5	x tgy + z sinx = y lnz	x² + y² + z² = z - 4
5.6		x² + y² + z² - 2xz = 2
5.7	z³ + 3xy + 3y = 7z	cosz + z tg²y + y ex = 6
5.8	x² + y² + z² = xyz + 4
5.9	x³ + y³ + z³ ­- 3xyz = 4
5.10	ex + x + 2y + z² = 4z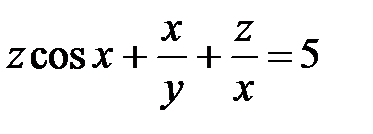
5.11	x² + 2y² + 3z² = 59
5.12		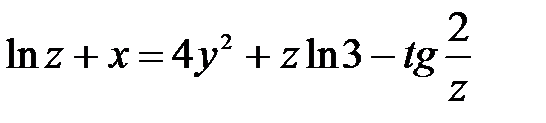x³ + 3xyz - z³ = 27
5.13		x + y ² + z³ - x³y²z = 2
5.14		x² + y² + z² - 2xy - 2yz - 2xz = 1
5.15	3x² + z ln5 - ctgxz = lny + 1
5.16
5.17
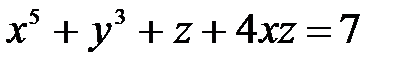
5.18	x² - 2y² + z² + 4x + 2z + 2 = 0;
5.19		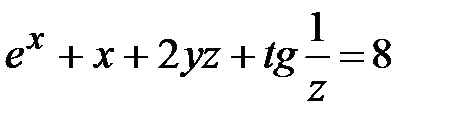x² + y² + z² - 4z = 8
5.20	3x² + 2y² - z² - xz + y = 2
5.21	x + y + z + 2 = xyz	x cosy - z tgx + y ctgz = 0
5.22	x² - 2xy - 3y² + 6x + z² - 8z = 20	x² + 2y² + z³ = e3xyz
5.23	z³ + 3xyz + 3y = 7x	x cosz + z tg²y + y ex = 6
5.24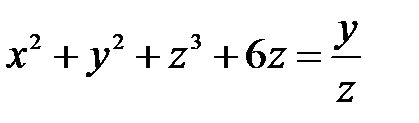
5.25	xyz + x³ + y³ + z³ = 7 + sin²xyz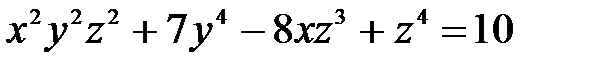
5.26	xzy² + 2z² + 3yz + 4 = 0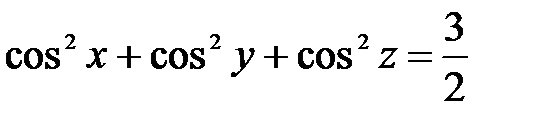
5.27		x² - 2y² + 3z² - yz + y = 2
5.28
5.29		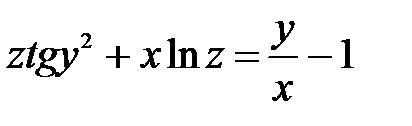x³ + 2y³ + z³ = 3xyz + 2y + 15
5.30

Задание 6. Найти частные производные 2-го порядка указанных функций:

6.1	z = arcsin(4y - 3x)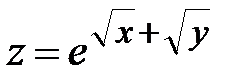
6.2		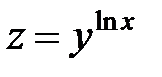z = arccos(4x y)
6.3		z = y ln(y² - x²)	z = arcsin(x - 5y)
6.4
6.5	z = ln(y² + x²)	z = arctg(x + y)	z = tgxy²
6.6	z = arctg(5x + 2y)		z = 2x²y - x³y2
6.7	z = x + arcctg(y + 2x)	z = sin²(y - 3x)	z = ctgx²y
6.8	z = arcsinxy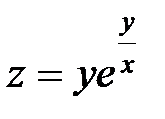
6.9			z = y² lnx
6.10	z = cos²(x + y)		z = ln(x² + y² + 2x - 4)
6.11	z = x lnxy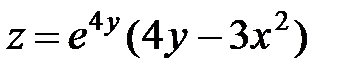
6.12		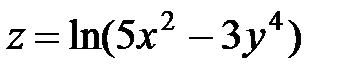z = arctg(2 - 3xy)
6.13	z = x tgy²
6.14			z = sin(3y² - x²)
6.15		z = ln(5xy - y²)
6.16		z = ln(x² + xy)
6.17		z = ln(x + y2)	z = exlny + lnx siny
6.18
6.19	z = arctg(2x - y)	z = x sinxy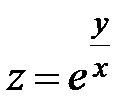
6.20		z = ln(3x² - 2y³)	z=y² tgx
6.21
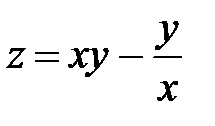
6.22	z = ln(4x² - 5y²)	z = xexsiny	z = arcctg(2x + 5y)
6.23	z = xy - 3x² - 2y² +10	z = arctg(2x² - y)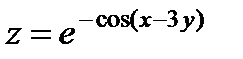
6.24	z = cos³(2x - y)
6.25
6.26	z = ln(x² + (y - 5)²)
6.27			.
6.28
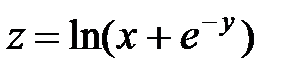
6.29	z = x² ln(y - 4)		z = x arcctg(x + 2y)
6.30	z =ex(siny + cosx)	z = (2x²y + y³)3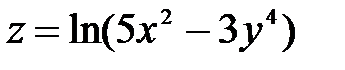

Задание 7. Исследуйте на экстремум следующие функции:

7.1	z = x³ + 8y³ - 6xy + 5	z = x² + 2y² - 4xy - 6x + 1
7.2	z = 2xy - 5x² - 3y² + 2	z = xy(12 - x - y)
7.3	z = x² - xy + y² + 9x - 6y + 20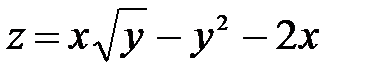
7.4	z = 1 + 15x - 2x² - xy - 2y²	z = x³ + 8y² - 6xy - 10
7.5	z = 8x³ - xy² + 6x² + y²	z = 2(x + y) - x² - y²
7.6	z = 2 - 5y² - 3x² + 2xy	z = 8 - 3x + 27y + x² - y²
7.7	z = 2x³ + 2y³ - 6xy - 5	z = e3x(3x - 2y²)
7.8	z = x³ + y³ - 6xy - 20
7.9	z = 1 + 6x - x² - xy - y²	z = 3x³ + 3y3 - 9xy + 10
7.10		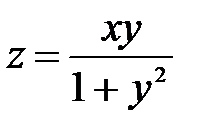z = x² + xy + y² - 6y - 1
7.11	z = e2x(x + y² + 2y)	z = xy - x² - y² - x - y
7.12	z = 4(x - y) - x² - y²
7.13	z = x²y - 8y³ - 6y² - x²	z = x² + y² - 2x - 2y
7.14	z = x² + y² + x + y - xy
7.15	z = x² + y² + xy - 3x - 6y	z = (y - 4)² - 3x²
7.16		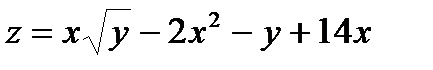z = x² + 3(y + 2)²
7.17	z = (x - 5)² + y² + 1	z = x² + 3y² + 4xy
7.18	z = 2xy - 2x² - 4y²	z = x³ + y³ - 3xy
7.19	z = x² + xy + y² - 6x - 1	z = x³ + y³ - 6xy - 63x + 18y
7.20	z = 6(x - y) - 3x² - 3y²	z = x² - xy + y² - 9x
7.21	z = x³ + y² - 3x - 6y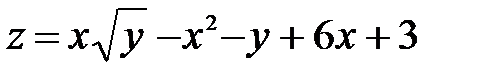
7.22	z = 2xy - 3x² - 2y² + 10	z = e2y(2y - 3x²)
7.23	z = 6xy - 2x³ - 2y³ - 5	z = xy -3x² + 2y² + 10
7.24		z = x³ + 3xy² - 15x + 12y
7.25	z = x³ + y² - 6xy - 39x + 18y + 20	z = (x - 2)² + 2y² - 10
7.26		z = x² + xy + y² + x - y + 1
7.27	z = x² + xy + y² - 6x - 9y	z = xy - x² - y² + 9
7.28	z = xy(x + y -12)	z = 6xy - x³ - 8y³ - 5
7.29	z = x² + y² - xy + x + y	z= xy(6 - x - y)
7.30	z= 4(x - 1)² + 5y² + 3	z = x² + xy + y² - 2x - y

Задание 8. Найдите наибольшее и наименьшее значения функции z = z(x,y) в области D, ограниченной заданными линиями:

8.1	z = x² + 2xy + 4x - y² D: x = 0, y = 0, x + y + 2 = 0	z = 3x² - x³ + 3y² + 4y D : x = 0, x = -1, y = 0, y = 2
8.2
8.3	z = 4(y - x) - x² - y²; D : x + 2y = 4, x - 2y = 4, x = 0.	z = x³ + y³ - 3xy; D : x = 0, y = 2, x = 2, y = 1.
8.4	z = xy - x - 2y D : x = 3, y = x, y = 0	z = x³ + 2xy - 4x + 8y D : x = 0, x = 1, y = 0, y = 2
8.5	z = 5x² - 3xy + y² - 4 D : x = -1, x = 1, y = -1, y =1	z = x² + 2xy - 4x + 8y D : y = x - 1, x = -3, y = 0
8.6
8.7	z = x² + y³ - 2x - 6y + 8 D : x = 0, y = 0, y = 1- x	z = 3xy - 5x² - y² + 4 D : x = -1, y = -1, x = 1, y = 1
8.8	z = y² + 2xy - 4y + 8x D : y = 0, x = 3, x - y + 1 = 0	z = x³ + y² - 3x + 2y D : x = 0, y = 0, x = 2, y = -2
8.9	z = 3x + y - xy D : y = x, y = 4, x = 0	z = x² + 2xy - 10 D : y = 0, y = x² - 4
8.10	z = 2xy + x² - Поделиться: Дата добавления: 2015-02-10; просмотров: 296; Мы поможем в написании вашей работы!; Нарушение авторских прав <== предыдущая лекция | следующая лекция ==> СЛОЖНЫЕ БЕССОЮЗНЫЕ ПРЕДЛОЖЕНИЯ. | Рабочая программа дисциплины