
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Образцы решения некоторых заданий контрольных работ
МАТЕМАТИКА
Методические рекомендации для студентов
решения задач по математики.
Пермь, 2011г.
Образцы решения некоторых заданий контрольных работ
Пример1. . Решить систему линейных уравнений, используя правило Крамера и метод обратной матрицы:

Решение.
1. Правило Крамера.
Находим определитель системы:

Следовательно, система является определённой. Для нахождения её решения вычисляем определители:



По формулам Крамера находим:



Ответ: 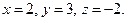
2. Метод обратной матрицы.
Введём обозначения: 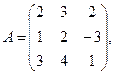

 Тогда систему можно переписать в виде матричного уравнения:
Тогда систему можно переписать в виде матричного уравнения:  , решение которого находим по формуле
, решение которого находим по формуле 
Прежде всего найдём матрицу  , обратную матрице
, обратную матрице  Определитель системы
Определитель системы 
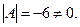 Следовательно для матрицы
Следовательно для матрицы  существует обратная. Вычислим алгебраические дополнения элементов этого определителя:
существует обратная. Вычислим алгебраические дополнения элементов этого определителя:









Отсюда 
Тогда 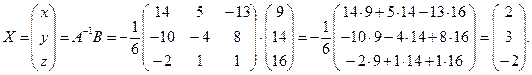
Итак,  Ответ:
Ответ: 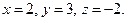
Пример2. Даны вершины треугольника АВС: 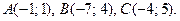 Построить треугольник на координатной плоскости. Найти:
Построить треугольник на координатной плоскости. Найти:
- периметр треугольника;
- уравнения всех сторон треугольника;
- уравнение высоты СН
- уравнение медианы АМ.
Решение.
1. Вычислим длины всех сторон треугольника:

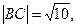

Следовательно, периметр треугольника ABC равен


Ответ: 
2. Составим уравнение прямой AB. Для этого воспользуемся уравнением прямой, проходящей через две точки:



Аналогично находим уравнения сторон BC:  AC:
AC: 
Ответ: AB: 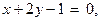 BC:
BC:  AC:
AC: 
3. Для нахождения уравнения высоты CH воспользуемся уравнением прямой с угловым коэффициентом и проходящей через заданную точку: 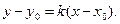 Известно, что условием перпендикулярности двух прямых является следующее условие:
Известно, что условием перпендикулярности двух прямых является следующее условие:  Так как прямые AB и CH перпендикулярны, то
Так как прямые AB и CH перпендикулярны, то  Используя координаты точки С, получаем уравнение высоты СH:
Используя координаты точки С, получаем уравнение высоты СH: 

Ответ: CH: 
4. Используя формулы для нахождения координат середины отрезка (полусумма соответствующих координат), найдем координаты точки M: 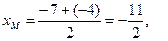
 тогда
тогда  . Используя уравнение прямой, проходящей через две точки A и M, получим уравнение медианы AM:
. Используя уравнение прямой, проходящей через две точки A и M, получим уравнение медианы AM:


Ответ: AM: 
Пример3. Даны координаты вершин пирамиды: A(4; 2; 5), B(0; 7; 2), C(0; 2; 7), D(1; 5; 0). Найти:
- площадь основания АВС пирамиды;
- объем пирамиды ABCD;
- общее уравнение плоскости АВС;
- уравнение ребра АD.
Решение.
1. Треугольник ABC построен на векторах  и
и  (для того чтобы найти координаты вектора, нужно из координат конца вычесть координаты его начала). Для вычисления площади основания ABC, найдём векторное произведение этих векторов:
(для того чтобы найти координаты вектора, нужно из координат конца вычесть координаты его начала). Для вычисления площади основания ABC, найдём векторное произведение этих векторов:  . Площадь треугольника ABC равна
. Площадь треугольника ABC равна  модуля векторного произведения векторов
модуля векторного произведения векторов  и
и 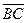 :
: 
Ответ: 
2. Пирамида ABCD построена на векторах  Объём пирамиды ABCD вычисляется как
Объём пирамиды ABCD вычисляется как  модуля смешанного произведения этих векторов:
модуля смешанного произведения этих векторов:  . Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то
. Так как смешанное произведение векторов равно определителю, составленному из координат этих векторов, то 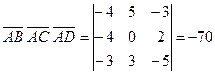 . Тогда
. Тогда 
Ответ: 
3. Воспользуемся уравнением плоскости, проходящей через три точки A, B и C:
 .
.
Раскрывая определитель и преобразуя полученное уравнение, получим общее уравнение плоскости ABC: x+2y+2z-18=0.
Ответ: ABC: x+2y+2z-18=0.
4. Для составления уравнения прямой AD нам понадобится точка, лежащая на этой прямой (можно взять точку A или D), и направляющий вектор этой прямой. В качестве направляющего вектора прямой AD можно взять вектор 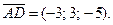 Тогда уравнение прямой AD имеют вид:
Тогда уравнение прямой AD имеют вид:
 .
.
Ответ: уравнение прямой AD:  .
.
Пример 4. Найти производную функции 
Решение. Воспользуемся правилами дифференцирования дроби, произведения и сложной функции:




Пример 5. Найти производную функции 
Решение. Воспользуемся правилом нахождения производной сложной функции:

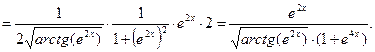
Пример 6. Провести полное исследование функции  и построить ее график.
и построить ее график.
Решение.
1)  , так как функция определена всюду, кроме точки x=1. В своей области определения функция непрерывна,
, так как функция определена всюду, кроме точки x=1. В своей области определения функция непрерывна,  является точкой разрыва графика функции; поведение функции в окрестности этой точки будет рассмотрено ниже.
является точкой разрыва графика функции; поведение функции в окрестности этой точки будет рассмотрено ниже.
2) Так как область определения не симметрична относительно точки x=0, то проверка на чётность и нечётность не проводится. График функции симметрией не обладает.
3) Найдём нули функции, т.е. точки пересечения с осями координат.
- При x=0 имеем:
 т.е. точка (0; 1) – точка пересечения с осью Oy.
т.е. точка (0; 1) – точка пересечения с осью Oy. - При y=0 имеем
 x= –1, т.е. точка (-1; 0) – точка пересечения с осью Ox.
x= –1, т.е. точка (-1; 0) – точка пересечения с осью Ox.
4) Найдём асимптоты графика функции.
- Вертикальные асимптоты: так как
 , то
, то  – вертикальная асимптота.
– вертикальная асимптота. - Горизонтальные асимптоты: так как
 , то горизонтальных асимптот нет.
, то горизонтальных асимптот нет. - Наклонные асимптоты: так как

 то
то 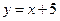 – наклонная асимптота.
– наклонная асимптота.
5) Найдём первую производную данной функции:
 .
.
Найдём точки, в которых первая производная равна нулю:  и не существует:
и не существует: 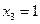 . Для исследования функции на экстремум применяем метод интервалов:
. Для исследования функции на экстремум применяем метод интервалов:

| 
| –1 | (–1; 1) | (1; 5) |  
| ||

| + | + | не существует | – | + | ||

|  
| нет экстремума | 
| нет экстремума | 
| точка минимума | 
|
Получаем, что при  график функции возрастает, при
график функции возрастает, при  - убывает. Точка
- убывает. Точка  - точка минимума,
- точка минимума, 
6) Найдём вторую производную данной функции:

Найдём точки, в которых вторая производная равна нулю :  и не существует:
и не существует: 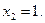 Для нахождения промежутков выпуклости и вогнутости графика функции, а также точек перегиба воспользуемся методом интервалов:
Для нахождения промежутков выпуклости и вогнутости графика функции, а также точек перегиба воспользуемся методом интервалов:

| 
| –1 | (–1; 1) |  
| |

| – | + | не существует | + | |

| 
| перегиб | 
| не существует | 
|
Получаем, что  - промежуток выпуклости,
- промежуток выпуклости, 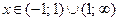 - промежуток вогнутости. Точка
- промежуток вогнутости. Точка  - точка перегиба,
- точка перегиба, 
Контрольные точки (нули функции, точки экстремума и точки перегиба) наносим на координатную плоскость и на основании проведённого исследования строим график данной функции.

Пример 7. Вычислить интеграл: 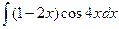 .
.
Решение. Применяя формулу интегрирования по частям  , получаем:
, получаем:


Пример 8. Вычислить интеграл:  .
.
Решение. Применяя к данному интегралу метод внесения под знак дифференциала, получаем: 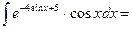


 . Ответ:
. Ответ: 
Пример 9. Вычислить интеграл: 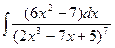
Решение. 
 Ответ:
Ответ: 
Пример 10. Вычислить площадь фигуры, ограниченной линиями:  .
.
Решение. Данная криволинейная трапеция получается при пересечении параболы и прямой. Найдем точки пересечения их графиков. Для этого решим совместно два уравнения  :
:  , откуда
, откуда 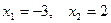 .
.
Сделаем схематический чертеж:
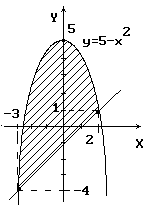
Тогда искомая площадь будет равна: 
 (ед2.).
(ед2.).
Ответ: 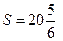 (ед2.).
(ед2.).
Пример11. Найти экстремум функции:  .
.
Решение. Находим частные производные первого порядка: 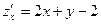 ,
,  . Находим точки возможного экстремума, для этого решаем систему уравнений:
. Находим точки возможного экстремума, для этого решаем систему уравнений:  , Таким образом, точка
, Таким образом, точка  - это точка, в которой может быть экстремум функции
- это точка, в которой может быть экстремум функции  .
.
Для проверки того, является полученная точка точкой экстремума или нет, и если является, то какой в этой точке будет экстремум: минимум или максимум, проверяем достаточное условие экстремума. Находим:  ,
,  и
и  . Составляем определитель
. Составляем определитель 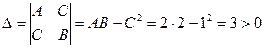 , следовательно в точке
, следовательно в точке 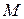 есть экстремум. Так как при этом
есть экстремум. Так как при этом 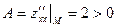 , то в точке
, то в точке  достигается минимум функции:
достигается минимум функции:  . Ответ:
. Ответ:  .
.
Пример12. Решить уравнение:  .
.
Решение. Данное уравнение относится к классу дифференциальных уравнений первого порядка с разделяющимися переменными. Разделим переменные:
 . Теперь уравнение можно интегрировать:
. Теперь уравнение можно интегрировать:  . Находим неопределенные интегралы:
. Находим неопределенные интегралы:  , откуда:
, откуда:  - это общий интеграл данного дифференциального уравнения. Ответ:
- это общий интеграл данного дифференциального уравнения. Ответ: 
Пример13. Решить уравнение  при условии
при условии  .
.
Решение. Данное уравнение является линейным дифференциальным уравнением первого порядка, для его решения применяем метод Бернулли. Делаем замену:  , где
, где  и
и  - неизвестные функции. Получаем:
- неизвестные функции. Получаем: 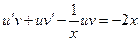 или
или  . Неизвестную функцию
. Неизвестную функцию 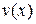 найдем из условия
найдем из условия  :
:  ,
,  , откуда
, откуда  . Тогда для нахождения второй неизвестной функции
. Тогда для нахождения второй неизвестной функции  нужно решить уравнение:
нужно решить уравнение:  , откуда:
, откуда:  . Тогда
. Тогда  и путем интегрирования последнего равенства получаем
и путем интегрирования последнего равенства получаем  . Тогда общее решение исходного уравнения имеет вид:
. Тогда общее решение исходного уравнения имеет вид: 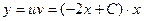 . Для нахождения частного решения воспользуемся начальным условием:
. Для нахождения частного решения воспользуемся начальным условием:  . Подставляя соответствующие значения переменных
. Подставляя соответствующие значения переменных  и
и  в общее решение, получаем:
в общее решение, получаем:  , откуда
, откуда  . Тогда частное решение данной задачи имеет вид:
. Тогда частное решение данной задачи имеет вид:  . Ответ:
. Ответ:  .
.
Пример14. Решить уравнение: у² +2 у' +5 у = 0.
Решение. Данное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Для его решения составляем характеристическое уравнение:  . Это алгебраическое уравнение второго порядка, его корни – комплексные, сопряженные числа:
. Это алгебраическое уравнение второго порядка, его корни – комплексные, сопряженные числа:  . Тогда общее решение данного уравнения имеет вид:
. Тогда общее решение данного уравнения имеет вид:  . Ответ:
. Ответ:  .
.
Пример15. Исследовать на сходимость ряд 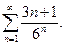
Решение. Для исследования данного ряда на сходимость можно применить признак Даламбера. Для этого находим  и
и  . Тогда:
. Тогда: 
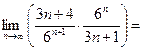
 , следовательно, по признаку Даламбера данный числовой ряд сходится.
, следовательно, по признаку Даламбера данный числовой ряд сходится.
Пример16. Найти область сходимости степенного ряда  .
.
Решение. Находим радиус сходимости ряда по формуле:  . Имеем:
. Имеем: 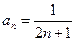 ,
,  . Тогда
. Тогда 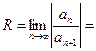
 . Итак, радиус сходимости
. Итак, радиус сходимости  . Тогда интервал сходимости данного ряда:
. Тогда интервал сходимости данного ряда:  , то есть
, то есть  .
.
Исследуем ряд на концах интервала сходимости.
При 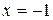 получаем числовой ряд
получаем числовой ряд  . Этот ряд знакочередующийся, для исследования его на сходимость применяем признак Лейбница:
. Этот ряд знакочередующийся, для исследования его на сходимость применяем признак Лейбница:
а) члены данного ряда убывают по абсолютной величине:  ;
;
б) 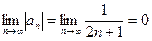 . Оба условия признака Лейбница выполняются, значит знакочередующийся числовой ряд сходится, и при
. Оба условия признака Лейбница выполняются, значит знакочередующийся числовой ряд сходится, и при  исходный степенной ряд сходится.
исходный степенной ряд сходится.
При  получаем числовой ряд
получаем числовой ряд  . Этот ряд знакоположительный, для исследования его на сходимость применяем интегральный признак Коши: составляем интеграл
. Этот ряд знакоположительный, для исследования его на сходимость применяем интегральный признак Коши: составляем интеграл 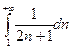 и исследуем его на сходимость. Имеем:
и исследуем его на сходимость. Имеем: 
 . Несобственный интеграл расходится, следовательно будет расходящимся и числовой ряд
. Несобственный интеграл расходится, следовательно будет расходящимся и числовой ряд  . Тогда на правом конце интервала сходимости исходный степенной ряд расходится. Вывод: степенной ряд сходится при
. Тогда на правом конце интервала сходимости исходный степенной ряд расходится. Вывод: степенной ряд сходится при 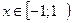 .
.
Ответ: степенной ряд  сходится при
сходится при 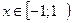 .
.
Пример17. Бросают три игральные кости. Найти вероятность того, что на верхних гранях появится число очков, сумма которых делится на пять.
Решение. Определим испытание и его результат, т. е. элементарное событие. Испытанием является бросание трех игральных костей; результатом – одно из сочетаний очков 1, ..., 6 на верхних гранях трех костей.
Исследуемое событие А – сумма очков на трех костях делится на пять. Вероятность события А вычислим с помощью формулы :
Р(А) = m/n.
Общее количество элементарных событий п можно найти по правилу умножения. На каждой игральной кости 6 граней и все они могут сочетаться со всеми гранями других костей. Итак, получаем n = 6 × 6 × 6 = 216.
Количество элементарных событий т, входящих в состав события А или благоприятствующих событию А,найдем выписав всевозможные результаты испытаний и оставив из них только те, для которых сумма очков на всех трех костях делится на пять. Можно облегчить работу, выписав всевозможные исходы бросания первых двух костей, сочетая с ними подходящие значения количества очков, выпавших на третьей кости. Имеем:
В результате получаем, что Р(т) = 43, значит, Р(А) = 43/216.
Ответ: Р(А) = 43/216.
Пример18. Вероятность выигрыша по одному билету равна 0,2. Имеется шесть билетов. Найти вероятности следующих событий: а) два билета будут выигрышными; б) выигрышных билетов будет от двух до четырех.
Решение. Для вычисления искомых вероятностей воспользуемся формулой Бернулли:  . По условию задачи
. По условию задачи  ,
,  .
.
а) Рассмотрим случайное событие А: два билета из шести будут выигрышными. Его вероятность:  .
.
б) Рассмотрим случайное событие В: выигрышных билетов будет от двух до четырех. Это сложное событие состоит из следующих:
В1: два билета из шести будут выигрышными;
В2: три билета из шести будут выигрышными;
В3: четыре билета из шести будут выигрышными.
Тогда В= В1+В2+В3 и Р(В) = Р(В1)+Р(В2)+Р(В3).
Находим по формуле Бернулли соответствующие вероятности:
 ,
,
 ,
,
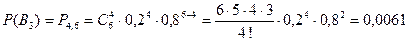 .
.
Тогда искомая вероятность: Р(В) = 0,2458+0,0492+0,0061=0,3011
Ответ: P(B)=0,3011.
Пример19. После обработки результатов эксперимента составлена таблица, в первой строке которой указаны группы возможных значений некоторой случайной величины хi , а во второй строке – численность каждой группы значений mi :
| х i | 21 | 17 | 35 | 11 |
| m i | 3 | 11 | 14 | 5 |
Найти объем выборки  ; относительные частоты
; относительные частоты  , соответствующие каждой отдельной группе значений случайной величины; составить вариационный ряд распределения данной случайной величины. Найти числовые характеристики выборки: среднее арифметическое, выборочную дисперсию и среднеквадратическое отклонение.
, соответствующие каждой отдельной группе значений случайной величины; составить вариационный ряд распределения данной случайной величины. Найти числовые характеристики выборки: среднее арифметическое, выборочную дисперсию и среднеквадратическое отклонение.
Решение. Найдем объем выборки n по формуле:  , где
, где  – число столбцов в таблице. Тогда n =3+11+14+5=33.
– число столбцов в таблице. Тогда n =3+11+14+5=33.
Относительные частоты  , соответствующие каждой отдельной группе значений случайной величины, находим по формулам:
, соответствующие каждой отдельной группе значений случайной величины, находим по формулам:  . Получаем:
. Получаем:  ,
, 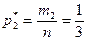 ,
,  ,
,  .
.
Составим вариационный ряд распределения данной случайной величины:
| х i | ||||

| 1/11 | 1/3 | 14/33 | 5/33 |
Находим числовые характеристики выборки:
а) среднее арифметическое находим по формуле:

б) выборочная дисперсия находится по формуле:  .
.
Получаем: 
в) среднеквадратическое отклонение:  .
.
Дата добавления: 2015-02-10; просмотров: 277; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| | | МЕТОДИЧЕСКОЕ УКАЗАНИЕ |