Стандартные ошибки выборок

Как уже отмечалось, выборочный метод позволяет результаты выборочной обработки материалов переносить на всю генеральную совокупность. При этом, естественно, имеет место некоторая ошибка, и эффективность выборочного метода заключается в том, что он позволяет оценить эту ошибку.

Ошибки, возникающие при использовании выборочных данных для суждения о всей совокупности, показывают, насколько хорошо характеристики выборки представляют соответствующие характеристики генеральной совокупности, и называются поэтому ошибками представительности (репрезентативности). Различают ошибки представительности двоякого рода: систематические и случайные.

Систематические ошибки возникают в том случае, если не выполнены условия случайности отбора.

Систематическая ошибка может возникнуть и в случае, когда формально отбор произведен случайным образом, но исходная совокупность не является полной и представительной для решения поставленной задачи.

В теории выборочного метода не рассматриваются систематические ошибки, но исследователь должен помнить о возможности их появления и принять меры, обеспечивающие их исключение. С помощью выборочного метода определяются величины ошибок второго рода, т. е. величины случайных ошибок.

Случайные ошибки выборок возникают за счет того, что для анализа всей совокупности используется только часть ее.

Хотя выборочный метод и позволяет обоснованно судить о средней арифметической некоторого количественного признака генеральной совокупности по средней арифметической, исчисленной по выборке, это, однако, не означает, что выборочная средняя совпадает с генеральной средней. Она, как правило, в той или иной степени от нее отличается.

Величина ошибки выборки представляет собой разность между генеральной и выборочной средними. Ошибки выборки различны для каждой конкретной выборки и в принципе могут быть обобщенно охарактеризованы с помощью средней из всех таких отдельных ошибок.

В математической статистике получены формулы, которые позволяют приближенно вычислить среднюю ошибку выборки, основываясь на данных только той выборки, которая имеется в распоряжении исследователя. Вычисление средней ошибки выборки зависит от способа отбора элементов из совокупности в выборку.

Средняя ошибка выборки при собственно случайном повторном методе отбора определяется формулой

(5.1)

где о — оценка среднего квдаратического отклонения в генеральной совокупности по выборке; n - число элементов в выборке (ее объем) (На практике величину а заменяют на среднее квадратическое отклонение выборки по формуле (4.7), но пользоваться этой формулой можно лишь при достаточно большом объеме выборки(n>30). Методы расчета средней ошибки для малых выборок изложены в § 4 этой главы.).

Как видим, средняя ошибка выборки (ее называют иногда стандартной ошибкой выборки) существенно зависит от среднего квадратического отклонения отдельных значений признака от выборочной средней: чем больше среднее квадратическое отклонение, т. е. чем больше разброс значений признака, тем, при прочих равных условиях, больше средняя ошибка выборки. Объем выборки воздействует на среднюю ошибку выборки в обратном направлении: чем больше численность выборки, тем меньше средняя ошибка выборки, что вполне объяснимо, так как большая выборка лучше представляет всю совокупность.

Средняя ошибка выборки при случайном бесповторном отборе находится по формуле

(5.2)

где N — объем генеральной совокупности.

Формула (5.2) отличается от формулы (5.1) только множителем— . Множитель всегда меньше единицы, в связи с чем средняя ошибка выборки при бесповторном способе отбора, как правило, бывает меньше средней ошибки повторной выборки того же объема. Это различие становится тем существеннее, чем большую долю генеральной совокупности составляет выборка. Если же отношение n/N мало, то множитель близок к единице и при расчете средней ошибки бесповторной выборки им можно пренебречь. Таким же образом следует поступать и в том случае, когда объем генеральной совокупности неизвестен, с чем историк может нередко столкнуться. Правда, при этом необходимо иметь хотя бы примерное представление о соотношении n и N.

Рассмотрим расчет средней (стандартной) ошибки выборки на конкретных примерах.

Пример 2. Из 2689 уставных грамот Тамбовской губернии необходимо сделать случайную 10%-ную выборку бесповторным способом и определить средние размеры дореформенного и пореформенного наделов на душу и соответствующие им средние ошибки выборки (Занесенные на специальные бланки материалы уставных грамот были любезно предоставлены авторам Б. Г. Литваком. Комплекс этих материалов, включающих данные о размерах дореформенного и пореформенного наделов, о форме эксплуатации, о величине высшего душевого надела и некоторые другие, возник в связи с отменой крепостного права и определял поземельные отношения крестьян и помещиков.).

Формирование выборки осуществим с помощью таблицы случайных чисел (табл. 9 приложения). Воспользуемся следующим способом, позволяющим рациональнее использовать таблицу случайных чисел. Из чисел от 3001 до 6000 будем вычитать 3000, а из чисел от 6001 до 9000 будем вычитать 6000. Из полученных чисел будем, как указывалось, отбирать те, которые не превосходят 2689. Так, первое число таблицы 5489 дает нам 2489, второе — 3522 дает 522 и т. д. В итоге получаем номера единиц совокупности, попавших в выборку.

Для дальнейшей работы полезно полученные числа расположить в возрастающем порядке. Во-первых, это облегчит отбор уставных грамот с соответствующими порядковыми номерами, во-вторых, выявит повторения, от которых нам нужно избавиться, так как выборка делается бесповторным способом. Исключение повторяющихся чисел приводит к тому, что количество отобранных чисел уменьшается. Обращаясь снова к таблице случайных чисел, доводим объем выборки до нужного размера.

Отобрав соответствующие уставные грамоты (их оказалось 264), переходим к расчету средних арифметических и соответствующих им средних ошибок выборки (В этом примере и во всех остальных примерах этой главы, базирующихся на материалах уставных грамот, мы из-за недостатка места не будем давать исходные данные, служащие для расчета выборочных характеристик, и ограничимся приведением результатов проделанных на их основе вычислений.).

Средний дореформенный надел на душу оказался равным 3,16 дес. (суммируем все наделы на душу и делим на число слагаемых — количество грамот):

Средний пореформенный надел на душу равен 2,71 дес. ( ). Чтобы воспользоваться формулой (5.2) для расчета средней ошибки выборки, необходимо предварительно вычислить средние квадратические отклонения по формуле (4.7);

?п=0,56.

Пользуясь полученными результатами и учитывая, что N =2689, имеем

?п=0,0328.

Поставленная задача полностью решена.

Пример 3. Из тех же 2689 уставных грамот Тамбовской губернии необходимо сделать случайную 10%-ную выборку повторным способом, определить средний размер дореформенного надела на душу по выборке и среднюю ошибку выборки

Техника подготовительной работы та же, что и в предыдущем примере, только повторно попавшие в выборку грамоты не исключаются. Результаты расчетов среднего размера дореформенного надела и среднего квадратического отклонения выборки по сформированной указанным способом выборке следующие:

?д=1,37.

Для расчета средней ошибки выборки воспользуемся формулой (5.1):

Итак, средняя ошибка выборки при повторном способе отбора оказалась большей (0,0846), чем при бесповторном (0,0798). Но разница между ними небольшая, так как отношение n к N невелико.

Средняя ошибка выборки при механическом способе отбора вычисляется по формуле случайной бесповторной выборки (5.2) или в случае, когда множителем можно пренебречь, по формуле случайной повторной выборки (5.1).

Пример 4. Генеральная совокупность та же, что и в предыдущих примерах Необходимо сделать 10%-ную механическую выборку, вычислить средний надел земли на душу до реформы и определить среднюю ошибку выборки.

Случайным образом отбираем в выборку одну уставную грамоту из первых десяти. По жребию выпало число 10. Следовательно, в выборку попадут грамоты с порядковыми номерами 10, 20, 30 и т. д.

Для этой выборки, включающей 263 элемента, средний размер дореформенного надела на душу (xд) равен 2,97 дес., а среднее квадратическое отклонение выборочных данных ?=1,48. Воспользовавшись формулой (5.2), определяем среднюю ошибку выборки:

Как правило, средняя ошибка выборки при механическом отборе оказывается меньше средней ошибки выборки при собственно случайном отборе.

Средняя ошибка выборки при типическом отборе определяется следующими формулами:

(5,3)

для повторной выборки и

(5,4)

для бесповторной выборки, где N — объем генеральной совокупности; Ni—объем i-й типической группы; ni—объем выборки из i-й типической группы; ?i— среднее квадратическое отклонение i-й типической группы; k — число типических групп.

Средняя арифметическая типической выборки рассчитывается по формуле

(5,5)

где —средняя арифметическая выборки из i-й типической группы; ni — объем i-й типической группы; N — объем генеральной совокупности.

Для того чтобы сделать типическую выборку, нужно прежде всего решить вопрос о том, каковы должны быть объемы выборки по каждой из выделенных типических групп. В зависимости от исследовательских задач и характера изучаемой совокупности, можно воспользоваться одним из следующих приемов.

Самый простой способ определения объема выборки из каждой типической группы, состоит в том, что объем всей намеченной выборки п делят на число типических групп k, т. е.

ni=n/k (5,6)

Второй, наиболее широко применяемый способ заключается в том, что объемы выборок из групп устанавливаются пропорционально объемам соответствующих типических групп, т. е.

В итоге для расчетов получается такая формула:

(5.7)

где ni — объем выборки из i-й типической группы; n — общий объем выборки из генеральной совокупности; Ni — объем i-й типической группы; N — объем генеральной совокупности.

Третий способ состоит в том, что число элементов в выборке для каждой типической группы определяется пропорционально средним квадратическим отклонениям соответствующих типических групп (?i), т. е. при определении ni руководствуются следующим соотношением:

Такой прием часто дает ощутимый выигрыш в точности. Сложность его использования состоит в том, что необходимо предварительно знать средние квадратические отклонения признака в типических группах, из которых будет извлекаться выборка. Для этого используются результаты расчетов по аналогичным данным либо делают пробные выборки из каждой группы и их средние квадратические отклонения кладут в основу расчета. Формула для расчета ni будет такой:

(5.8)

где σ_i, — среднее квадратическое отклонение i-й группы; — сумма средних квадратических отклонений всех групп; n — объем выборки.

Наконец, четвертый способ образования типической выборки учитывает и размеры типических групп (Ni) и колеблемость признака в этих группах (?i); при формировании выборки исходят из того, что

Формула для расчета ni, четвертым способом такова:

где Ni — объем i-й типической группы; ?i — среднее квадратическое отклонение i-й группы; n—общий объем выборки из генеральной совокупности; k— число типических групп.

Из указанных четырех способов определения численности выборок из типических групп самым простым, но и самым несовершенным является первый. Несложен для расчетов второй способ. Его целесообразно применять в тех случаях, когда типические группы резко отличаются по объему. Если типические группы имеют примерно одинаковый объем, то лучше формировать выборки с учетом рассеивания признака, т. е. третьим способом. Если, наконец, объемы типических групп различны и заметно отличны их средние квадратические отклонения, то наилучшие результаты достигаются при применении четвертого способа.

Рассмотрим теперь на примерах методику вычисления средних арифметических типических выборок и возникающих при этом стандартных ошибок.

Случайный отбор элементов из типических групп может проводиться двумя способами. Если типические группы в исходных данных разделены и каждая имеет собственную нумерацию, то случайный отбор элементов до нужного объема производится из каждой группы отдельно. Если же элементы типических групп расположены в генеральной совокупности вперемешку, как в нашем случае, то отбор осуществляется из всей совокупности, при этом следят, чтобы объемы отдельных групп не были превышены. Случайные числа, соответствующие элементам тех групп, объемы выборок по которым достигнуты, отбрасываются.

Пример 5. Из совокупности уставных грамот Тамбовской губернии сделать 10%-ную типическую выборку с учетом численности групп. Вычислить средний пореформенный надел на душу и среднюю ошибку выборки.

При знакомстве с уставными грамотами обращает на себя внимание тот факт, что надел земли на душу после реформы тяготеет к высшему душевному наделу. Естественно предположить, что типические группы, образованные с учетом размера высшего душевого надела, будут более однородными, чем вся совокупность в целом.

Разобьем всю совокупность на три группы. К первой группе отнесем селения с размером высшего душевого надела, равным 3,00 дес., ко второй — 3,25 дес., к третьей — 3,50 дес. Объемы групп будут равны соответственно 1717, 445 и 525 (Две грамоты мы не учитываем, так как в одной из них указан высший размер душевого надела, равный 2,0 дес., в другой—2,75 дес., в результате чего общий объем совокупности составил N1+N2+N3=2687 грамот.).

Получены следующие результаты расчетов средних характеристик по каждой из трех групп выборки:

для первой группы (высший душевой надел—3,00 дес.)

для второй типической группы (высший душевой надел — 3,25 дес.)

для третьей типической группы (высший душевой надел — 3,50 дес.)

Пользуясь соответствующими формулами табл. 2, имеем окончательно:

Средняя ошибка выборки, полученная таким способом, оказалась несколько меньше средней ошибки выборки, полученной при случайном отборе. В данном случае различие типических групп невелико. При больших различиях групп выигрыш в точности, даваемый типическим отбором, бывает более существенным.

Пример 6. Определить объемы выборок каждой типической группы так, чтобы они оказались пропорциональными средним квадратическим отклонениям соответствующих групп. Совокупность и общий объем выборки те же, что и в предыдущем примере.

Воспользуемся промежуточными результатами примера 5:

Тогда по формуле (5.8) объемы выборок типических групп будут такими:

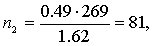
т. е. из первой типической группы (высший размер душевого надела равен 3,00 дес.) следует отобрать 86 грамот, из второй типической группы (высший размер душевого надела — 3,25 дес.) — 81 грамоту, из третьей типической группы (высший размер душевого надела — 3,50 дес.) — 102 грамоты.

Пример 7. Генеральная совокупность и критерий, по которому происходит деление на типические группы, те же, что и в предыдущих двух примерах. Сделать типическую 10%-ную выборку, отбирая количество элементов в типических группах пропорционально численности этих групп и средним квадратическим отклонениям.

Рассчитать средний пореформенный надел на душу и среднюю ошибку выборки.

По формуле (5.9) численность выборок из типических групп будет следующей:

Аналогично рассчитываются n2 и n3: n2=41, n3=60.

Следовательно, из первой типической группы нужно взять 168 грамот, из второй — 41 грамоту, из третьей — 60. Отобрав требуемое количество грамот (техника отбора была изложена выше), переходим к вычислению интересующих нас характеристик.

Результаты расчета средних по группам следующие:

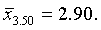
Соответствующие им средние квадратические отклонения равны:

.

Средний по всей выборке пореформенный надел на душу равен (по формуле (5.5)):

Для расчета средней ошибки выборки воспользуемся соответствующей формулой из сводной табл. 2:

Средняя ошибка выборки получилась меньше, чем при случайном методе отбора, но несколько больше соответствующей характеристики, полученной для типической выборки, образованной пропорционально численности типических групп. Последнее произошло, надо полагать, потому, что типические группы по размеру высшего душевого надела отличаются, в основном, по численности и значительно меньше—по разбросу признака.

Сведем воедино итоги рассмотренных примеров, чтобы еще раз сравнить полученные результаты (см. табл. 1).

В целом приведенные примеры подтверждают установленные в статистике общие положения. Важнейшим для применения выборочного метода в исторических исследованиях является то, что наиболее точные результаты дает типический отбор. Стандартная ошибка средней при этом методе отбора получается меньшей, чем при случайном и механическом отборе (сравним процентные отношения ошибок к средним арифметическим). При этом следует иметь в виду, что размеры наделов крестьян являются признаком, рассеивание которого является небольшим. При большей неоднородности изучаемых совокупностей данных преимущества типического отбора будут еще очевиднее. Что касается собственно случайного и механического отбора, то они в общем дают близкие результаты. Надо лишь всегда проверять, насколько механический отбор является близким к случайному. Принципиальных различий между бесповторным и повторным случайным отбором нет.

Для удобства пользования формулы выборочного метода, применяемые для вычисления выборочных средних арифметических и их стандартных ошибок при разных видах отбора, сведены в табл. 2. В эту таблицу не вошли формулы для расчета средних ошибок выборок при многоступенчатом способе отбора (Эти сведения можно найти в кн.: Йейтс Ф. Выборочный метод в переписях и обследованиях.). Что касается многофазного отбора, то он равносилен взятию выборок различных объемов для разных признаков и ничего нового в вычислительные процедуры не вносит.

Таблица 2. Формулы выборочного метода для средней арифметической при различных видах отбора.

	Выборочная средняя	Объем выборки из типических групп	Средняя ошибка выборки ?
при повторном отборе	при повторном отборе
Собственно случайный отбор и механический отбор (При механическом отборе применяется формула бесповторной выборки, за исключением тех случаев, когда множителем можно пренебречь.)
Типический отбор: а) при равных объемах выборки из всех типических групп б) при объемах выборки, пропорциональных средним квадратическим отклонениям типических групп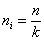
Эти формулы являются одновременно и общим для всех случаев типического отбора
в) при объемах выборки, пропорциональных объемам типических групп
г) при объемах выборки, пропорциональных объемам типических групп и их средним квадратическим отклонениям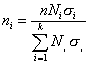

Таблица 3.Формулы выборочного метода для доли признака при различных видах отбора.

	Выборочная средняя	Объем выборки из типических групп	Средняя ошибка выборки ?
при повторном отборе	При повторном отборе
Собственно случайный отбор и механический отбор (При механическом отборе применяется формула бесповторной выборки, за исключением тех случаев, когда множителем можно пренебречь.)
Типический отбор: а) при равных объемах выборки из всех типических групп б) при объемах выборки, пропорциональных средним квадратическим отклонениям типических групп
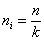
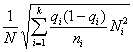
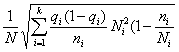
Эти формулы являются одновременно и общим для всех случаев типического отбора
в) при объемах выборки, пропорциональных объемам типических групп
г) при объемах выборки, пропорциональных объемам типических групп и их средним квадратическим отклонениям

Средняя ошибка выборки для доли признака. Выборочный метод позволяет оценить не только среднюю арифметическую генеральной совокупности, но и долю некоторого (качественного или количественного) признака во всей совокупности.

Доля признака во всей совокупности (q) вычисляется как отношение числа элементов, обладающих этим признаком (No), к числу элементов всей совокупности (N), т. е. q=Nо/N.

Отметим, что рассмотренная выше теория и методика применения выборочного метода для расчета средней может быть применена и для расчета доли без каких-либо принципиальных изменений.

Сводка всех формул выборочного метода для доли признака дана в табл. 3.

Пример 8. На основе 10%-ной случайной бесповторной выборки из совокупности уставных грамот Тамбовской губернии вычислить доли селений с системой эксплуатации крестьян; а) оброчной, б) барщинной и в) смешанной, а также соответствующие им средние ошибки выборки

Из 264 грамот, составивших 10%-ную случайную бесповторную выборку, грамот, описывающих селения с оброчной, барщинной и смешанной системами эксплуатации, оказалось соответственно 51, 197 и 16 Тогда выборочная доля селений с оброчной системой эксплуатации равна qоб=51:264=0,19, выборочные доли селений с барщинной и смешанной системами эксплуатации равны соответственно 0,75 и 0,06.

Воспользовавшись формулой для собственно случайной бесповторной выборки из табл. 3, рассчитаем средние ошибки выборки для доли:

?б=0,03; ?ом=0,01

Точность и надежность выборочного метода: предельные ошибки. Определение объема выборки

Предельная ошибка выборки и доверительный интервал. Средняя ошибка выборки дает некоторое представление об ошибке репрезентативности, т. е. об ошибке, с которой выборочная средняя представляет действительное значение генеральной средней. Именно она показывает, какова будет ошибка в среднем, если из одной и той же генеральной совокупности сделать много выборок одинакового объема. Однако в каждой конкретной выборке ошибка может существенно отличаться от средней ошибки, т. е. нет гарантии, что ошибка, которая действительно была допущена в конкретном выборочном исследовании, не превышает средней ошибки.

Поэтому гораздо полезнее было бы знать те границы, в которых «практически наверняка» находится действительная ошибка, допущенная в данной конкретной выборке. Эти границы (пределы) указываютсяпредельной ошибкой выборки (обозначим ее Δ). Предельная ошибка выборки показывает тот предел, которого практически наверняка не превосходит действительная ошибка. Иначе говоря, предельная ошибка Δ показывает действительно допущенную ошибку с избытком, с превышением (возможно, очень значительным) и тем самым гарантирует, что действительная ошибка не превосходит Δ.

Предельная ошибка Δ вычисляется на основе знания средней ошибки μ по формуле

(5,10)

где t — величина, вычисляемая по специальной таблице. Обратим внимание на то, что в определении предельной ошибки постоянно употреблялись слова «практически наверняка». Необходимо пояснить смысл понятия «практическая уверенность».

Установленный предел Δ для ошибки выборки лишь указывает, что если из генеральной совокупности сделать много выборок, то для подавляющего большинства из них ошибка выборки не превысит вычисленного нами предела Δ. При этом, правда, могут быть все-таки и такие выборки, у которых ошибка выборки больше Δ, и не исключено, что конкретная выборка входит в их число. Однако можно точно измерить степень уверенности в том, что ошибка конкретной выборки не превысит Δ. Для этого нужно указать долю выборок, у которых ошибка выборки не превосходит Δ. Обозначим эту долю выборок через Р, где . Чем ближе Р к единице, тем больше будет уверенность в том, что ошибка конкретной выборки не превышает Δ (Читатель, знакомый с понятием вероятности, заметит, что вместо слов «степень уверенности» можно использовать термин «вероятность».). На практике используются, например, значения, равные 0,68; 0,95; 0,99 и некоторые другие.

Значением Р фактически измеряется надежность результатов выборочного исследования: для значений Р, достаточно близких к единице, практически исключается возможность того, что генеральная средняя будет отличаться от вычисленной выборочной средней больше чем на Δ. Со своей стороны Δ указывает точность, гарантируемую заданным уровнем надежности Р. Таким образом, предельная ошибка выборки позволяет одновременно и взаимосвязано указать точность и надежность результатов выборочного исследования.

В математической статистике доказано, что распределение выборочных средних при достаточно больших n подчиняется нормальному закону (см. § 3, гл. 4) со средним значением, равным генеральной средней , и средним квадратическим отклонением, равным средней ошибке выборки μ. Значит, для достаточно больших выборок, вероятность Р того, что отклонение выборочной средней от генеральной средней не превысит по модулю предельной ошибки, т. е. или можно найти по табл. 1 приложения (где Ф(t) соответствует Р).

Эта же таблица позволяет решать и обратную задачу: по заданной вероятности Р найти величину предельной ошибки Δ, которая соответствует Р, другими словами, найти точность, соответствующую данному уровню надежности. Какова, например, предельная ошибка, соответствующая надежности 0,9545? По табл. 1 приложения найдем значение t, соответствующее вероятности Ф(t)= 0,9545. Оказывается, t=2. С вероятностью 0,9545 отклонение выборочной средней от генеральной по модулю не превосходит Δ=2μ, т. е. не выше двукратной средней ошибки выборки.

Разумеется, всегда желательно обеспечить большую надежность результатов, поэтому надо стараться выбрать Р возможно ближе к 1. Однако необходимо учитывать, что с возрастанием надежности увеличивается и t, а значит, и предельная ошибка Δ=tμ, т. е. падает точность результатов, что может оказаться по тем или иным соображениям недопустимым. Поэтому на практике приходится довольствоваться некоторым компромиссом между противоречивыми требованиями максимальной надежности и максимальной точности. Если такого компромисса достичь не удается и надежность и точность неудовлетворительны, следует сделать вывод, что объем выборки недостаточен и необходимо произвести новую выборку большего объема или же дополнить старую.

Знание предельной ошибки выборки позволяет указать и пределы для генеральной средней. Действительно, поскольку выборочная средняя отличается от генеральной средней (практически наверняка) не более чем на Δ, то

или, иначе,

(5.11)

Таким образом, с помощью вычисления выборочной средней и предельной ошибки выборки можно указать интервал, в котором практически наверняка находится генеральная средняя (так называемый доверительный интервал). При этом всегда указывается надежность Р этого результата (то значение Р, которое использовалось в вычислении Δ).

Пример 9. Вычислить предельные ошибки выборки по результатам примера 2 § 1 и определить пределы для генеральной средней.

Выборочная средняя для дореформенного надела равна 3,16, средняя ошибка выборки—0,0798.

Пусть Р=0,9545. Этому значению Р по табл. 1 приложения соответствует t=2. Пользуясь формулой (5.10), имеем Δ=2*0,0798=0,1596=0,16, т. е. предельная ошибка выборки равна приблизительно 0.16.

Переходим к определению пределов. Чтобы вычислить нижний предел, нужно из выборочной средней вычесть предельную ошибку выборки:

3,16—0,16=3,00.

Верхний предел получаем, прибавив к выборочной средней предельную ошибку:

3,16+0.16=3,32.

Тогда имеем следующие пределы для генеральной средней :

Результаты можно интерпретировать так: с надежностью (вероятностью) 0,95 генеральная средняя будет не меньше 3,00 дес. и не больше 3,32 дес. Или, другими словами, если выборки повторять много раз, то в 95 случаях из 100 получим, что выборочная средняя будет отстоять от генеральной средней не далее, чем на величину вычисленной нами предельной ошибки, равной 0,16 дес.

Возьмем теперь Р= 0,9876=0,99. Тогда t=2,5,.

и генеральная средняя заключена в следующих пределах:

.

Пределы для генеральной средней расширились, но зато увеличилась степень доверия к результатам: уже примерно в 99 случаях из 100 мы не ошибаемся, указывая эти границы для средней.

Как правило, в исторических исследованиях рассмотренный в примере уровень надежности (Р=0,95; P=0,99) оказывается достаточным.

Порядок вычисления предельной ошибки выборки для доли признака ничем не отличается от вычисления предельной ошибки для средней арифметической.

Определение объема выборки. Вопрос об определении объема выборки является в выборочном методе исходным, ибо всякая выборка имеет заданный объем.

Заметим сразу, что зачастую исследователь лишен возможности решать вопрос об объеме выборки либо в силу ограниченности имеющихся в его распоряжении данных (естественные выборки), либо в силу тех или иных технических причин.

В тех же случаях, когда постановка вопроса об определении объема выборки возможна, его решение производится в следующем порядке.

Прежде всего производится пробная выборка произвольного объема. При этом можно пойти по одному из двух различных путей. Во-первых, можно попытаться сразу угадать нужный объем выборки, основываясь на каких-либо соображениях разумности объема выборки (например, можно попробовать 10%- или 20%-ную выборку). В случае если объем этой выборки окажется недостаточным, можно будет впоследствии дополнить эту выборку до нужного объема.

При втором подходе пробная выборка берется совсем небольшой (как правило, 1% и менее от объема генеральной совокупности). При этом практически следует руководствоваться некоторым компромиссом между требованием достаточной репрезентативности выборки и желанием уменьшить объем предварительных расчетов. На основе этой пробной выборки по приведенной ниже формуле (5.12) определяется необходимый объем окончательной выборки. Далее уже можно делать выборку заданного объема и проводить по ней выборочное исследование.

Анализ пробной выборки начинается с вычисления выборочной средней (Полезно вычислить и среднее квадратическое отклонение признака в пробной выборке, чтобы получить представление о величине разброса признака генеральной совокупности.). Исходя из знания величины этой cредней, а также учитывая содержание изучаемой проблемы и конкретные особенности исследования, определяется требуемая точность к оценке генеральной средней (требования к точности задаются с помощью предельной ошибки выборки Δ). Кроме того, задается уровень надежности результатов (требования к надежности задаются с помощью Р — степени уверенности в том, что отклонения выборочной средней от генеральной средней не превысят заданной предельной ошибки Δ).

Например, если =10, то ясно, что примерно такой же величины будет и генеральная средняя (если разброс признака не слишком велик). Задавшись точностью, скажем, в 5%, определим допустимую предельную ошибку:

Δ=10*5/100==0,5.

Далее, зададимся уровнем надежности результатов. Выберем, например, Р=0,95.

Заметим, что стремясь к большей точности и надежности результатов, не следует излишествовать в этом направлении, так как может оказаться, что для достижения поставленных требований придется брать выборку объемом во всю совокупность. При этом теряет смысл само применение выборочного метода. Как правило, такие повышенные требования к результатам не оправдываются целями исследования и без ущерба для дела можно остановиться на более умеренных ограничениях. В том же случае, когда высокие требования вытекают из целей исследования и вычисленный объем выборки оказывается порядка объема всей совокупности, следует сделать вывод о том, что в данном случае применение выборочного метода нецелесообразно.

Рассчитав характеристики пробной выборки, переходят к оценке результатов этой выборки. Если используется первый путь исследования (относительно большой пробной выборки), то задав предельную ошибку Δ, следует сравнить ее с предельной ошибкой, вычисленной по пробной выборке Δпр (при одном и том же значении Р). Если окажется, что Δпр<=Δ то пробной выборки вообще достаточно, она может рассматриваться в качестве основной и ее результаты служат результатами всего выборочного исследования. Если же Δпр> Δ, что нередко имеет место при втором пути исследования, то определяют необходимый объем выборки по следующей формуле:

(5.12)

где σ2 — дисперсия признака, вычисленная по пробной выборке; Δ— заданная точность результатов выборочного исследования (заданная предельная ошибка выборки); t — величина, которая находится по табл. 1 приложения исходя из заданной надежности Р результатов выборочного исследования.

Заметим, что если пробная выборка мала (n<30), то для определения t используется табл. 2 приложения. В ней при определении t учитывается также объем пробной выборки (для нахождения табличного значения t берется объем пробной выборки, предварительно уменьшенный на единицу). Кроме того, в том случае и вычисляется так, как указано в § 4 этой главы.

Отметим, что приведенная формула дает общий объем выборки приближенно. Поэтому желательно если есть возможность, еще несколько увеличить объем выборки по сравнению с вычисленным.

Сделав окончательную выборку найденного объема, следует обязательно проверить, совпадает ли ее предельная ошибка с заданной, т. е. удовлетворяются ли заданные требования к точности и надежности результатов. В том редком случае, когда окажется, что действительная предельная ошибка существенно больше заданной (это может произойти из-за нерепрезентативности пробной выборки), придется еще раз повторить процедуру определения объема выборки уже на основе полученных более полных и точных данных.

Приведем также формулу для нахождения необходимого объема выборки при определении доли признака:

(5.13)

где t и Δ имеют тот же смысл, что и в предыдущей формуле,a q — доля признака в пробной выборке.

Рассмотрим пример, поясняющий основные моменты решения задачи об определении объема выборки.

Пример 10. Воспользовавшись данными по предприятиям европейской России за 1879 г. (См.: Указатель фабрик и заводов европейской России/Сост. П. А. Орлов. Спб., 1881, вып. 1. В «Указателе» содержатся сведения по фабрикам и заводам со стоимостью производимой продукции свыше 2 тыс. руб. (всего около 12000 предприятий).), определить объемы выборок, необходимые для расчетов средней стоимости произведенной продукции в расчете на одного рабочего на предприятиях: а) с паровыми двигателями, б) без паровых двигателей.

Сделаем сначала пробную 1%-ную выборку (случайным бесповторным способом) (Из-за недостатка места выборочные данные не приведены). Отметим, что среди предприятий, попавших в выборку (128 предприятий), 87 составляют предприятия без паровых двигателей и 41 —с паровыми двигателями.

Пользуясь выборочными данными, вычисляем по каждому типу предприятий среднюю стоимость произведенной на одного рабочего продукции , среднее квадратическое отклонение σ, среднюю ошибку выборки μ и предельную ошибку выборки Δ при уровне надежности P=0,95.

Для предприятий без паровых двигателей получаем соответственно (тыс. руб.); ;

Для предприятий с паровыми двигателями получим (тыс. руб); ; ; . Отсюда для генеральных средних вычисляются следующие пределы:

для предприятий без паровых двигателей

для предприятий с паровыми двигателями

При сопоставлении полученных результатов напрашиваются следующие выводы: средняя стоимость продукции на одного рабочего на предприятиях без паровых двигателей и на предприятиях с паровыми двигателями различна, причем на предприятиях с паровыми двигателями она заметно выше. Однако, строго говоря, такой вывод пока еще неправомерен и может рассматриваться лишь как гипотеза. Дело в том, что доверительные интервалы для генеральных средних по предприятиям без паровых двигателей (1,1; 1,7) и по предприятиям с паровыми двигателями (1,4; 3,4) пересекаются, так что средние генеральные вполне могут совпадать или даже находиться в соотношении, противоположном высказанной гипотезе.

Нетрудно заметить, что указанная неопределенность результатов получается главным образом в силу того, что предельная ошибка выборки по предприятиям с паровыми двигателями Δ2 слишком велика. В самом деле, различие между выборочными средними по двум типам предприятий составляет

Поэтому, чтобы попытаться подтвердить и обосновать высказанную выше гипотезу, достаточно, чтобы предельные ошибки выборок для обеих групп предприятий (Δ1, Δ2) не превышали половины этой разности, т. е. 0,5, тогда доверительные интервалы не будут пересекаться.

Отметим, что предельная ошибка выборки по предприятиям без паровых двигателей Δ=0.3 вполне удовлетворительна. Чтобы обеспечить предельную ошибку выборки, равную 0,5, для другой группы предприятий, рассчитаем необходимый объем выборки из совокупности предприятий с паровыми двигателями. Выбирая t по табл. 1 приложения, соответствующие значению Р= 0,9545, и пользуясь формулой (5.12), получим

Дополнив теперь выборку из группы предприятий с паровыми двигателями до рассчитанного объема, получим новые значения средней, среднего квадратического отклонения, средней и предельной ошибок выборки:

Сравним интервалы для генеральных средних. Для предприятий без паровых двигателей используем результат пробной выборки (которая оказалась для этой группы предприятий и окончательной):

А для предприятий с паровыми двигателями имеем после увеличения объема выборки

.

Как видим, теперь доверительные интервалы действительно не пересекаются и высказанная выше гипотеза о том, что средняя стоимость продукции на одного рабочего существенно больше для предприятий с паровыми двигателями, получает убедительное и надежное подтверждение. Другими словами, данные, использованные в примере 10, свидетельствуют о том, что внедрение машин повышало производительность труда.

Интересно отметить, что для достижения нужной точности и надежности результатов из совокупности предприятий с паровыми двигателями нам пришлось сделать примерно в два раза большую выборку, чем из группы предприятий без паровых двигателей. Это объясняется тем, что для предприятий с паровыми двигателями существенно больше разброс изучаемого признака, что вполне естественно для прогрессивной технологии, применяемой на этих предприятиях.

В заключение отметим еще один поучительный факт, с которым мы столкнулись в рассмотренном примере. По предприятиям с паровыми двигателями первоначальный объем выборки составлял 41 единицу, при этом обеспечивалась точность, определяемая предельной ошибкой выборки, равная единице (Δ2=1). Такая точность, как оказалось, была недостаточной, потребовалась в два раза большая точность—Δ2`=0.5. Это привело к тому, что объем новой выборки составил 164 единицы, что в четыре раза больше первоначального.

Следовательно, необходимый объем выборки растет пропорционально квадрату требуемой точности, что следует прямо из формулы (5.12). А так как квадраты чисел при возрастании самих чисел возрастают очень быстро, то повышенные требования к точности могут привести к неумеренному росту объема выборки. Поэтому важно, чтобы требования к точности выборочного исследования всегда диктовались целями и содержанием исследования. В рассмотренном примере такой целью было обоснование содержательной научной гипотезы.

§ 4. Малые выборки

Рассмотренные выше приемы расчета ошибок выборки основаны на доказанном в математике факте нормальности распределения выборочных средних. Однако этот факт имеет место только при достаточно большом объеме выборки n. Если пользоваться изложенными приемами при п меньшем 20, могут возникнуть грубые ошибки.

Выборки, объем которых меньше 20—30 единиц совокупности, будем называть малыми (Четкой границы между большой и малой выборками в общем случае указать невозможно. Выборка, сделанная из совокупности с небольшим разбросом признака, может считаться большой, тогда как выборка такого же объема, произведенная из более разнородной совокупности, окажется малой. Вопрос о том, к какой категории отнести выборку, решается в каждом конкретном случае). Для расчета ошибок таких выборок используется несколько иной математический аппарат.

Средняя ошибка малой выборки вычисляется по формуле

(5.14)

где S — оценка среднего квадратического отклонения в генеральной совокупности по малой выборке. Она равна:

(5.15)

где σ вычисляется по формуле (4.7); n — объем выборки;k — число вариант, т. е. S несколько отличается от оценки среднего квадратического отклонения в генеральной совокупности по большой выборке, см. (5.1).

Пример 11. В табл. 4 приведены данные о размерах оброка в конце XVIII в. (в руб. серебром на муж. душу). Первая выборка состоит из 16 уездов нечерноземной полосы, вторая выборка—из 16 уездов черноземной полосы. Перед нами две «естественные выборки», которые можно рассматривать как случайные, т. е. репрезентативные Требуется рассчитать выборочные средние и средние ошибки выборок.

Вычисляем последовательно средние арифметические, средние квадратические отклонения малых выборок, и, наконец, стандартные ошибки выборок Получаем:

для нечерноземной полосы

для черноземной полосы

Заметим, что в пределах интересующей нас точности вычислений поправка на малую выборку не изменила величины стандартной ошибки. Заметное различие появляется при вычислении предельной ошибки выборки.

Предельная ошибка малой выборки вычисляется по формуле

(5.16)

где t рассчитывают исходя из так называемого закона распределения Стьюдента с k степенями свободы (в отличие от больших выборок, где t вычисляется на основе нормального закона распределения).

Связь между t и вероятностью (уровнем надежности) Р в распределении Стьюдента сложнее, чем в нормальном распределении и опосредствуется через объем выборки. При возрастании объема выборки распределение Стьюдента приближается к нормальному, практически с ним совпадая при достаточно больших n.

При вычислении предельной ошибки малой выборки значение t(k) определяется по таблице распределения Стьюдента с k степенями свободы (табл. 2 приложения), с учетом заданного уровня надежности Р и объема выборки (для подстановки в таблицу фактический объем выборки надо предварительно уменьшить на единицу: k=n—1).

Пример 12. Используя данные предыдущего примера, найти предельные ошибки выборки для средних размеров оброка с уровнем надежности P=0,9 и Р=0,95 и определить границы для генеральной средней.

Обращаясь к табл. 2 приложения и учитывая, что при объеме выборки, равном 16, k, используемое для нахождения табличного значения t, равно 16—1=15, а заданный уровень надежности—0,9, находим t (15) =1,75.

Тогда предельная ошибка выборки для среднего размера оброка нечерноземной полосы по формуле (5.16) будет равна

Следовательно, границы генеральной средней таковы:

т. е. с вероятностью 0,9 средний размер оброка в нечерноземной полосе не выйдет за указанные границы.

Предельная ошибка второй выборки (для размеров оброка в черноземной полосе) и границы генеральной средней находятся аналогично. Имеем:

Чтобы получить более достоверные результаты, возьмем большую вероятность (уровень надежности). Пусть Р=0,95, тогда из табл. 2 приложения найдем t (15)=2,13, и для нечерноземной полосы

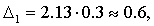
для черноземной полосы

.

Итак, в конце XVIII в. средний размер оброка в черноземной полосе выше, чем средний размер оброка в нечерноземной полосе. Важно, что границы, в которых заключены средние, не пересекаются. Это свидетельствует о том, что различие размеров оброка в двух районах имело не случайный, а закономерный характер.

Для более строгих выводов о существенности различия между двумя выборочными средними есть специальные методы, изложенные в гл. 9 (§2 — критерии для средних, § 3 — критерии для дисперсий). Так, если имеются две выборочные средние и относящиеся к двум различным совокупностям, причем , то можно предположить, что и генеральные средние этих совокупностей различны. Специальный критерий, основанный на распределении Стьюдента, позволяет для фиксированного уровня надежности Р и числа степеней свободы k=n1+n2-2 сделать вывод о значимости или незначимости различия между выборочными средними. В § 2 гл. 9 на данных примера 11 выясняется, что полученное различие между средними размерами оброка у крестьян черноземной и нечерноземной полосы в конце XVIII в. является значимым. Заметим, что проверяя гипотезу о существенности различия средних, пользуются предположением о том, что разброс признака в обеих совокупностях примерно одинаков. Это предположение также можно проверить (см. гл. 9, § 3, пример 11).

Отметим, что в тех же разделах гл. 9 рассмотрены аналогичные критерии для больших выборок, которые вместо распределения Стьюдента используют нормальное распределение, поскольку при возрастании объема выборки распределение Стьюдента стремится к нормальному.

В заключение скажем несколько слов о больших и малых выборках. Различать большие и малые выборки необходимо, но точной границы между ними установить нельзя. Важно иметь в виду, что к большим выборкам можно применять аппарат теории малых выборок, тогда как обратное приводит к значительным ошибкам. В сомнительных случаях для получения надежных результатов рекомендуется пользоваться аппаратом малых выборок.

В больших выборках средние теснее группируются около генеральной средней, что позволяет получать более точные и надежные результаты, тогда как в малых выборках приходится довольствоваться более широкими границами для средних или меньшей достоверностью результатов. Тем не менее теория малых выборок нашла в практике широкое распространение и применяется даже в тех случаях, когда во власти исследователя сделать выборку большой (См., например: Дружинин Н. К. Выборочный метод и его применение в социально-экономических исследованиях М., 1970, с. 77.).

Историку обычно не приходится выбирать между формированием большой или же малой выборки, поскольку он часто имеет дело с естественными малыми "выборками, число которых он не может изменить, т. е. он стоит перед альтернативой: либо воспользоваться данными малой выборки для анализа исследуемых явлений, либо отказаться от такого анализа. Обработка этих выборок методами математической статистики позволяет в ряде случаев (когда само использование выборочного метода возможно) обоснованно решить вопрос о правомерности или неправомерности тех или иных выводов и заключений на основе имеющихся материалов. И в том и в другом случае исследование приобретает более объективный и глубокий характер, нежели при традиционных методах.

Для того чтобы применить выборочный метод к естественным выборкам, необходимо доказать тем или иным способом случайность образования имеющейся выборки. В проверке случайности выборки ведущая роль принадлежит традиционным методам содержательного источниковедческого анализа. Отсутствие преднамеренности в порядке сбора и хранения тех сведений, след от которых остался в виде естественной выборки, свидетельствует о случайности последней. Математические методы позволяют дополнить этот анализ (см. гл. 9).

И наконец, последнее замечание. В этой главе мы ограничились оценкой средней арифметической генеральной совокупности с помощью характеристик, вычисленных по выборке. Но выборочный метод позволяет решать и более сложные вопросы анализа совокупностей. В частности, по выборке можно судить о наличии или об отсутствии связи между признаками, о форме связи. К процедурам выборочного метода мы будем обращаться при необходимости в соответствующих разделах курса.