Визначення надійності системи в цілому

________________________________

________ ___________________

(підпис) (ініціали і прізвище)

___ ___ 20__ р.

20_
Зміст

Вступ……………………………………………………………..…………..……3

1. Побудова системи за заданими компонентами, визначення

її структури та зв’язків між елементами………………..……………..……4

2. Визначення показників надійності елемента системи ……….……..…....8

3. Визначення надійності системи в цілому………………......………..……10

Висновки………………………………………………………..……………….13

Список використаних джерел………………………………………………….14

У вступі необхідно вказати основні положення щодо використання теорії систем на залізничному транспорті, а також основні методи, які використовуються при аналізі складних систем.

_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

.

1 Побудова системи за заданими компонентами, визначення її структури та зв'язків між елементами.

Система – це ________________________________________.

Якщо кожна частина системи зв’язана з іншою частиною таким чином, що зміна в одній частині викликає змінe у всіх інших частинах і у всій системі, то система поводиться ______________, або як ціле. Якщо частини зовсім не зв'язані між собою, то зміна в кожній частині залежить винятково від цієї частини. Таке поводження системи називається ____________, або фізично __________. Цілісність системи оцінюється мірою системності:

(1)

де - безліч необхідних станів;

- безліч можливих функціональних станів;

- операція перетинання множин;

- операція об'єднання множин.

Можна навести 4 основні схеми взаємодії:

1)

2)

3)

4)

Елементи і компоненти, входи і виходи по різному зв'язані між собою. Існують такі види зв'язків: ________________________________.

________________ зв'язки формуються за допомогою зворотнього зв'язку: тобто зв'язок між входом і виходом того ж самого елемента системи. Зворотній зв'язок, що зменшує вплив вхідного сигналу на вихідний, називається ____________, а той, що збільшує цей вплив, називається ____________. _____________ зворотній зв'язок сприяє відновленню рівноваги в системі, що порушена зовнішнім впливом. _______________ зворотній зв'язок підсилює відхилення від стану рівноваги в системі.

Замкнуті зв'язки бувають наступних типів:

а).

б).

в).

1)

2)

Складні зв'язки. У складних системах виникає безліч комбінацій зв'язків між окремими елементами і підсистемами. Найбільш поширені:

1).

2).

3).

Найбільш важливим питанням при аналізі складної системи є визначення її структури. Можна виділити наступні структури:

1). _____________________:

2).______________________:

3). ___________________:

4). ___________________:

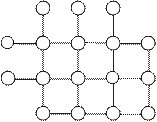
У роботі 1 необхідно побудувати структурну схему залізничної станції або її інформаційної системи відповідно до завдання (додаток 1, завдання 1).

Рис. 1 - Структурна схема системи.

2 Визначення показників надійності елемента системи

Кожна окремо взята система характеризується надійністю. Надійність системи – це її здатність до безвідмовної роботи протягом заданого проміжку часу у визначених умовах. У теорії надійності розрізняють два типи відмов – раптова та поступова відмова. Раптова відмова – це миттєвий вихід з ладу у випадковий момент часу. Поступова відмова пов'язана з поступовим погіршенням характеристик системи, і як тільки параметри системи виходять за визначені межі, система вважається такою, що відмовила.

У даній роботі розглядається раптова відмова системи. Для її описання використовується експоненційний закон

,

де – імовірність безвідмовної роботи елемента;

– інтенсивність потоку відмов, яка є єдиним параметром потоку відмов для експоненційного закону надійності.

Середній час безвідмовної роботи елемента визначається як:

Також можна сказати, що це час, за який імовірність безвідмовної роботи елемента зменшується в разів.

Для визначення параметру проведемо тест за планом випробувань (N=12, U, r=10). Цей план означає, що загальна кількість елементів, які будуть використані під час тесту дорівнює N=12, після відмови будь якого елемента він не замінюється новим, умовою завершення тесту є відмова r=10 елементів.

Для даного плану тесту параметр визначається за формулою:

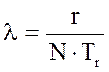
де - час, протягом якого відмовили елементів.

Згідно завдання необхідно визначити інтенсивність потоку відмов і середній час безвідмовної роботи елемента, побудувати графіки емпіричної функції надійності і емпіричної функції ненадійності елемента, графік теоретичної функції надійності і теоретичної функції ненадійності елемента.

Вихідними даними для виконання завдання є таблиця часів відмов елементів при виконанні тесту, яка наведена у додатку 1.

l = ------------- =

T₀ = -------- =

Рисунок 2. - Графік емпіричної функції надійності і емпіричної функції ненадійності елемента.

Рисунок 3. - Графік теоретичної функції надійності і теоретичної функції ненадійності елемента.

Визначення надійності системи в цілому

Нехай система S складається з n елементів, показники надійності яких відомі. Визначимо надійність системи. Вона залежить від того, як елементи об'єднані в систему, тобто від її структури.

Розглянемо систему без резервування, тобто відмова будь-якого елемента призводить до відмовлення системи в цілому. Щодо надійності така структура рівносильна послідовному з'єднанню елементів.

Нехай P – надійність системи S, а P_i – надійності елементів Э_i (рисунок 3)

Рисунок 4 – Послідовне з’єднання елементів

Нехай елементи відмовляють незалежно один від одного, тоді за правилом множення імовірностей незалежних подій маємо:

,

або . (5)

Якщо , то .

Резервні елементи включаються в систему паралельно тим, надійність яких недостатня. Нехай елементи Э₁ і Э₂ незалежні по відмовах, а відповідні надійності (імовірності безвідмовної роботи) дорівнюють Р₁ і Р₂, знайдемо (рисунок 4).

Рисунок 5 – Паралельне з’єднання елементів

Розглянемо імовірність відмови системи . Щоб подія (відмова всієї системи) відбулася, необхідно, щоб відмовили обидва елементи, тобто за правилом множення імовірностей незалежних подій маємо:

, (6)

використовуючи поняття ненадійності системи і ненадійності елементів маємо:

, (7)

де – відповідні ненадійності елементів (імовірність того, що елемент відмовить), які визначаються як .

Тоді маємо:

;

. (8)

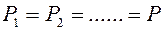Якщо число дублюючих один одного незалежних елементів дорівнює n, то надійність системи , якщо , то .

Для оцінки надійності складної структури, що включає в себе послідовні та паралельні об’єднання елементів, доцільно поділити систему на ряд підсистем, що не мають загальних елементів. На рисунку 5 наведений приклад розподілення складної системи семи елементів. Тут підсистема І містить два елементи, що пов’язані послідовно, підсистема ІІ – два паралельно зв’язаних елементи, підсистема ІІІ об’єднує послідовно І та ІІ підсистеми, IV підсистема – два паралельно зв’язаних елементи, V підсистема послідовно поєднує IV підсистему з п’ятим елементом.

Рисунок 6 – Складна система з паралельними та послідовними зв’язками між елементами

Відповідно до формул (5,8) отримуємо

(9)

Вихідними даними є структурна схема, що наведена на рисунку 6 і значення надійності елементів, що наведені в таблиці 3. Потрібно розрахувати надійність системи.

Рис. 7 – Структурна схема.

Таблиця 3 – Надійність елементів системи

Розрахуємо надійність системи за формулами 5 та 8: