
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа № 1
Таблица выбора вариантов индивидуального задания
| Вариант | Номера задач | |||||||||
1. При прямолинейном движении зависимость пройденного телом пути от времени описывается уравнением S=A+Bt+Ct2+Dt3, где В=2 м/с , С=0,14 м/с2, D=0,1 м/с3. Через сколько времени после начала движения ускорение тела будет равно а) 1 м/с2; б) 6 м/с2? Чему равна средняя скорость тела за промежуток времени, в течение которого ускорение возросло от 1 м/с2 до 6 м/с2?
2. Зависимость координаты тела от времени задана уравнением x=At+Bt2+Ct3, где A=12 м/c, B=-3 м/с2, C=-4 м/c3. Найти в явном виде зависимость скорости и ускорения от времени; расстояние, пройденное телом, мгновенные скорость и ускорение тела через 2 секунды после начала движения; среднюю скорость за промежуток времени от t1=2c до t2=5с.
3. Две материальные точки движутся согласно уравнениям: x1=A1t+B1t2+C1t3; x2=A2t+B2t2+C2t3, где А1=4 м/с, В1=8 м/с2, С1=-16 м/с3; А2=2 м/с, В2=-4 м/с2, С2=1 м/с3. В какой момент времени ускорения этих точек будут одинаковы? Найти скорости точек в этот момент. Найти среднюю скорость второй материальной точки за промежуток времени с момента начала движения до момента равенства их ускорений.
4. Движения двух материальных точек выражаются уравнениями: x1=A1t+B1t2+C1t3; x2=A2t+B2t2+C2t3, где А1=20 м/с, В1=2 м/с2, С1= -4 м/с3; А2=2 м/с, В2=2 м/с2, С2=0,5 м/с3. В какой момент времени скорости этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента равенства их скоростей.
5. Движение материальной точки задано уравнением x=Аt+Вt2, где А=4 м/с, В=-0,05 м/с2. Определить момент времени, в который скорость точки равна нулю. Найти путь, пройденный точкой, координату и ускорение точки в этот момент. Найти среднюю скорость точки за промежуток времени с момента начала движения до момента равенства ее скорости нулю.
6. Движения двух материальных точек выражаются уравнениями:x1=A1+B1t2+C1t3; x2=A2t+B2t2+C2t3, где А1=-12 м, В1=-2 м/с2, С1= 8 м/с3; А2=-4 м/с, В2=-3 м/с2, С2=8 м/с3. В какой момент времени координаты этих точек будут одинаковыми? Определить скорости и ускорения точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента равенства их координат.
7. Уравнение движения тела имеет вид х=15t - 0,4t2. Определить промежуток времени после начала движения, в течение которого точка вернется в исходное положение. Найти путь, пройденный точкой и ее среднюю скорость за этот промежуток времени.
8. Уравнение движения материальной точки по прямой имеет вид х=А+Вt+Сt2, где А=4 м, В=2 м/с, С=-0,5 м/с2. Для момента времени t1=2 секунды определить координату точки и мгновенное ускорение. Найти путь, пройденный точкой, и среднюю скорость за промежуток времени от t1=2с до t2=6с.
9. Зависимость пройденного телом пути от времени дается уравнением S=A-Bt+Ct2+Dt3, где А=6 м, В=3м/с, С=-2 м/с2, D=0,2 м/с3. Считая движение прямолинейным, определить для тела в интервале времени от t1=1 c до t2=4 с 1) среднюю скорость; 2) путь, пройденный телом; 3) в какой момент времени после начала движения точка вернется в исходное положение?
10. Две материальные точки движутся согласно уравнениям:x1=A1t +C1t3; x2=A2t+B2t2+C2t3, где А1=14 м/с, С1=-6 м/с3; А2=2 м/с, В2=4 м/с2, С2=-5 м/с3. В какой момент времени t1 ускорение первой точки будет вдвое больше ускорения второй? Найти скорости точек в этот момент. Найти среднюю скорость первой точки за промежуток времени с момента начала движения до момента времени t1.
11. Тело некоторой массы скользит вниз по наклонной плоскости с постоянным ускорением, равным 0,05g. Найти угол наклона этой плоскости, если коэффициент трения равен 0,02.
12. За какое время тело спустится с вершины наклонной плоскости высотой 3 м и углом у основания  , если максимальный угол у основания наклонной плоскости, при котором тело находится на ней в покое, равен
, если максимальный угол у основания наклонной плоскости, при котором тело находится на ней в покое, равен  ?
?
13. Тело массой m скользит по наклонной плоскости, образующей с горизонтом угол 45  . Зависимость пройденного телом пути от времени дается уравнением s=Ct2, где С=1,73 м/с
. Зависимость пройденного телом пути от времени дается уравнением s=Ct2, где С=1,73 м/с  . Найти коэффициент трения тела о плоскость.
. Найти коэффициент трения тела о плоскость.
14. На автомобиль массой 1т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с ускорением 1 м/с2 в гору с уклоном 1 м на каждые 25 м пути.
15. По наклонной плоскости с углом  наклона к горизонту, равным 30
наклона к горизонту, равным 30  , скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения
, скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения  =0,15.
=0,15.
16. С каким ускорением будет скользить тело по наклонной плоскости, образующей с горизонтом угол  =24
=24  , если коэффициент трения равен 0,03? Какое время потребуется для прохождения при этих условиях пути 100 м? Какую скорость тело будет иметь в конце пути?
, если коэффициент трения равен 0,03? Какое время потребуется для прохождения при этих условиях пути 100 м? Какую скорость тело будет иметь в конце пути?
17. С вершины клина, длина которого l=2 м и высота h=1 м, начинает скользить небольшое тело. Коэффициент трения между телом и клином  =0,15. Определить: 1) ускорение, с которым движется тело; 2) время прохождения тела вдоль клина; 3) скорость тела у основания клина.
=0,15. Определить: 1) ускорение, с которым движется тело; 2) время прохождения тела вдоль клина; 3) скорость тела у основания клина.
18. На автомобиль массой 2т во время движения действует сила трения, равная 0,1 действующей на него силы тяжести. Найти силу тяги, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью в гору с уклоном 1 м на каждые 25 м пути.
19. Тело некоторой массы равномерно скользит вниз по наклонной плоскости. Найти угол наклона этой плоскости, если коэффициент трения равен 0,05.
20. Тело скользит по наклонной плоскости, образующей с горизонтом угол 45  . Пройдя путь 36,4 см, тело приобретает скорость 2 м/с. Найти коэффициент трения тела о плоскость.
. Пройдя путь 36,4 см, тело приобретает скорость 2 м/с. Найти коэффициент трения тела о плоскость.
21. Маховик, момент инерции которого равен J=63,7 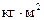 , вращается с постоянной угловой скоростью
, вращается с постоянной угловой скоростью 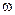 =31,4 рад/с. Найти тормозящий момент М, под действием которого маховик останавливается через t=20 с. Маховик считать однородным диском.
=31,4 рад/с. Найти тормозящий момент М, под действием которого маховик останавливается через t=20 с. Маховик считать однородным диском.
22. Определить, какая постоянная касательная сила приложена к ободу однородного сплошного диска радиусом 0,5 м и массой 24 кг, если при вращении на него действует момент сил трения 2  . Угловое ускорение диска постоянно и равно 16 рад/
. Угловое ускорение диска постоянно и равно 16 рад/  .
.
23. Маховое колесо, имеющее момент инерции 245 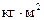 , вращается, делая 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти момент сил трения.
, вращается, делая 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти момент сил трения.
24. К ободу однородного сплошного диска радиусом R=0,2 м приложена постоянная касательная сила F=98,1 Н. При вращении на диск действует момент сил трения 5  . Найти массу диска, если известно, что диск вращается с постоянным ускорением
. Найти массу диска, если известно, что диск вращается с постоянным ускорением  =100 рад/
=100 рад/  .
.
25. Маховик в виде сплошного диска, момент инерции которого J=150 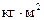 , вращается с частотой
, вращается с частотой 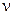 =240 об/мин. Через время t=1 мин как на маховик стал действовать момент сил торможения, он остановился. Определить момент сил торможения.
=240 об/мин. Через время t=1 мин как на маховик стал действовать момент сил торможения, он остановился. Определить момент сил торможения.
26.Вал массой m=100 кг и радиусом R 5 см вращался с частотой 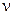 =8
=8 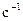 . К цилиндрической поверхности вала прижали тормозную колодку с силой N=40 Н, под действием которой вал остановился через t=10 с. Определить коэффициент трения.
. К цилиндрической поверхности вала прижали тормозную колодку с силой N=40 Н, под действием которой вал остановился через t=10 с. Определить коэффициент трения.
27. Диск массой m=2 кг и радиусом R=10 см вращается вокруг оси, проходящей через его центр. Уравнение движения диска имеет вид  , где
, где  . Определить вращающий момент М в момент времени t=2 с, если момент сил торможения постоянен и равен 12
. Определить вращающий момент М в момент времени t=2 с, если момент сил торможения постоянен и равен 12  .
.
28.Маховик радиусом 0,5 м, вращаясь равнозамедленно, за 10 секунд изменил частоту вращения от 480 до 120 об/мин. Тормозящий момент постоянен и равен 40  . Определить массу маховика.
. Определить массу маховика.
29. К шару радиусом 0,2 м приложена касательная сила 100 Н. При вращении вокруг оси, проходящей через центр масс, на шар действует момент сил трения 5  . С каким угловым ускорением вращается шар, если его масса 15 кг?
. С каким угловым ускорением вращается шар, если его масса 15 кг?
30. Маховик в виде сплошного диска, момент инерции которого J=1,5 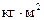 , вращаясь при торможении равнозамедленно, за время t=1 мин уменьшил частоту своего вращения с
, вращаясь при торможении равнозамедленно, за время t=1 мин уменьшил частоту своего вращения с  =240 об/мин до
=240 об/мин до  =120 об/мин. Определить момент силы торможения.
=120 об/мин. Определить момент силы торможения.
31. На нитях одинаковой длины, равной 2,5 м, закрепленных в одной точке, подвешены два шарика массами 75 г и 100 г, соответственно. Нить с большим шариком отклонили на угол 60 градусов и отпустили. Считая удар абсолютно неупругим, определить, на какую высоту поднимутся шарики после соударения.
32. Пуля массой 15 г, летящая с горизонтальной скоростью 0,5 км/с, попадает в баллистический маятник1) массой 6 кг и застревает в нем. Определить высоту, на которую поднимется маятник, откачнувшись после удара.
33. Два тела массами 3 кг и 5 кг движутся навстречу друг другу со скоростями 7 м/с и 9 м/с. Найти скорость движения тел после соударения и выделившуюся при неупругом ударе энергию.
34. Пуля массой 15 г, летящая горизонтально со скоростью 200 м/с, попадает в баллистический маятник1) длиной 1 м и массой 1,5 кг и застревает в нем. Определить угол отклонения маятника.
35. Тело массой 3 кг движется со скоростью 2 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе.
36. Пуля массой 12 г, летящая с горизонтальной скоростью 0,6 км/с, попадает в мешок с песком массой 10 кг, висящий на длинной нити, и застревает в нем. Определить: 1) высоту, на которую поднимется мешок, отклонившись после удара; 2) энергию, израсходованную на пробивание песка.
37. На нитях одинаковой длины, равной 0,8 м, закрепленных в одной точке, подвешены два шарика массами 40 г и 60 г, соответственно. Нить с меньшим шариком отклонили на угол 60 градусов и отпустили. Считая удар неупругим, определить, какая энергия пошла на нагревание шариков.
38. Пуля массой 9 г, летящая с горизонтальной скоростью 0,6 км/с, попадает в баллистический маятник1) массой 8 кг и застревает в нем. Определить выделившуюся при этом энергию.
39. Тело массой 8 кг движется со скоростью 3 м/с и ударяется о движущееся со скоростью 1 м/с в том же направлении тело вдвое большей массы. Считая удар центральным и неупругим, определить количество теплоты, выделившееся при ударе.
40. На нитях одинаковой длины, равной 1,2 м, закрепленных в одной точке, подвешены стальной и пластилиновый шарики одного размера массой 20 г и 8 г, соответственно. Нить со стальным шариком отклонили на угол 45 градусов и отпустили. Определить, на какую высоту поднимутся шарики после соударения.
41. Частица движется со скоростью v=0,8c, где с – скорость света в вакууме. Определить: 1) отношение массы релятивистской частицы к ее массе покоя; 2) релятивистский импульс и полную энергию, если эта частица – электрон.
42. Определить, на сколько процентов масса релятивистской частицы, вылетающей из ускорителя со скоростью v=0,75c, где с – скорость света в вакууме, больше ее массы покоя. Определить кинетическую энергию этой частицы, если она – протон.
43. Определить скорость движения релятивистской частицы, если ее масса в два раза больше массы покоя. Найти полную энергию этой частицы, если ее масса совпадает с массой покоя ядра атома гелия.
44. Определить релятивистский импульс, полную и кинетическую энергии протона, если скорость его движения v=0,8c, где с – скорость света в вакууме.
45. Полная энергия релятивистской частицы в 8 раз превышает ее энергию покоя. Определить скорость этой частицы и релятивистский импульс, если предположить, что эта частица – нейтрон.
46. Определить скорость и релятивистский импульс электрона, если его кинетическая энергия равна энергии покоя.
47. Определить массу, кинетическую и полную энергии протона, движущегося со скоростью v=0,75c, где с – скорость света в вакууме.
48. Определить релятивистский импульс и полную энергию альфа – частицы, кинетическая энергия которой равна 3,6. 10 -9 Дж.
49. Определить скорость движения протона, при которой его кинетическая энергия равна 7,7. 10 –11 Дж. Найти его релятивистский импульс и полную энергию.
50. Определить релятивистский импульс, кинетическую и полную энергии нейтрона, движущегося со скоростью v=0,95c, где с – скорость света в вакууме.
51.Определить скорость и ускорение материальной точки через 5 с после начала движения, если она совершает гармонические колебания, согласно уравнению  , м. Написать уравнение для силы, вызывающей это движение, если масса точки 11 г.
, м. Написать уравнение для силы, вызывающей это движение, если масса точки 11 г.
52.Точка массой 20 г совершает гармонические колебания с амплитудой 10 см и периодом 5 с под действием некоторой периодической силы. Определить для точки максимальные скорость, ускорение и действующую силу.
53. Определить максимальную скорость точки, совершающей гармонические колебания по закону 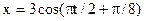 ,м. Найти массу этой точки, если максимальная сила, вызывающая эти колебания, равна 12 Н.
,м. Найти массу этой точки, если максимальная сила, вызывающая эти колебания, равна 12 Н.
54. Скорость материальной точки, совершающей гармонические колебания, задается уравнением  , м/с. Записать зависимость смещения этой точки от времени. Найти силу, действующую на точку в момент времени t=6 с, если масса точки 4 г.
, м/с. Записать зависимость смещения этой точки от времени. Найти силу, действующую на точку в момент времени t=6 с, если масса точки 4 г.
55. Определить скорость и ускорение материальной точки через 3 с после начала движения, если она совершает гармонические колебания согласно уравнению  , м. Найти силу, действующую на точку через 20 с после начала движения, если масса точки 2 г.
, м. Найти силу, действующую на точку через 20 с после начала движения, если масса точки 2 г.
56. Амплитуда гармонических колебаний материальной точки равна 5 см, период - 4 с. Найти максимальные скорость и ускорение колеблющейся точки. Найти силу, действующую на точку через 2 с после начала движения, если масса точки 10 г, а начальная фаза равна 1200.
57.Уравнение движения материальной точки  , см. Найти максимальную скорость точки и ее максимальное ускорение, а также силу, действующую на эту точку в начальный момент времени, если масса точки 7 г.
, см. Найти максимальную скорость точки и ее максимальное ускорение, а также силу, действующую на эту точку в начальный момент времени, если масса точки 7 г.
58. Уравнение движения материальной точки 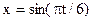 ,м. Найти моменты времени, в которые достигаются минимальные по модулю скорость и ускорение. Найти силу, действующую на точку через 10 с после начала движения, если масса точки 12 г.
,м. Найти моменты времени, в которые достигаются минимальные по модулю скорость и ускорение. Найти силу, действующую на точку через 10 с после начала движения, если масса точки 12 г.
59.Определить максимальные по модулю значения скорости и ускорения материальной точки, совершающей гармонические колебания с амплитудой 3 см и угловой частотой 
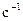 . Найти силу, действующую на точку через 3 с после начала движения, если масса точки 30 г, а начальная фаза колебаний 600.
. Найти силу, действующую на точку через 3 с после начала движения, если масса точки 30 г, а начальная фаза колебаний 600.
60.Точка совершает колебания по закону  , где А=5 см,
, где А=5 см,  . Определить ускорение точки в момент времени, когда ее скорость равна 8 см/с. Написать уравнение для силы, вызывающей это движение, если масса точки 9 г.
. Определить ускорение точки в момент времени, когда ее скорость равна 8 см/с. Написать уравнение для силы, вызывающей это движение, если масса точки 9 г.
61.На концах тонкого стержня длиной 30 см укреплены одинаковые грузы по одному на каждом конце. Стержень с грузами колеблется около горизонтальной оси, проходящей через точку, удаленную на 10 см от одного из концов стержня. Определить приведенную длину и период колебаний такого физического маятника. Массой стержня пренебречь.
62.На стержне длиной 30 см укреплены два одинаковых груза: один в середине стержня, другой - на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину и период колебаний такой системы. Массой стержня пренебречь.
63.Математический маятник длиной 40 см и физический маятник в виде тонкого прямого стержня длиной 60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние от центра масс стержня до оси колебаний.
В задачах 64 - 67 физический маятник представляет собой тонкий однородный стержень массой m с укрепленным на нем маленьким шариком массой m. Маятник совершает колебания около горизонтальной оси, проходящей через точку 0 на стержне. Определить период гармонических колебаний маятника, изображенного на рисунке. Длина стержня L= 1 м. Шарик рассматривать как материальную точку.
 |  | 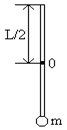 |  |
64. 65. 66. 67.
В задачах 68 - 70физический маятник представляет собой тонкий однородный стержень массой m с укрепленными на нем двумя маленькими шариками массами m и 2m. Маятник совершает колебания около горизонтальной оси, проходящей через точку 0 на стержне. Определить частоту гармонических колебаний маятника, изображенного на рисунке. Длина стержня L = 1 м. Шарики рассматривать как материальные точки.

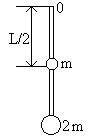 68. 69. 70.
68. 69. 70.

В задачах 71- 80 в сосуде вместимостью V=0,01  содержится смесь двух газов массами
содержится смесь двух газов массами  и
и  при температуре Т. Определить давление р , концентрацию n и плотность
при температуре Т. Определить давление р , концентрацию n и плотность  смеси газов.
смеси газов.
71. Кислород m1=20 г и азот m2=3 г, Т=400 К;
72. Кислород m1=15 г и водород m2=2 г, Т=300 К;
73. Азот m1=7 г и водород m2=1 г, Т=280 К;
74. Гелий m1=6 г и кислород m2=7 г, Т=420 К;
75. Углекислый газ m1=17 г и кислород m2=9 г, Т=500 К;
76. Гелий m1=3 г и водород m2=2 г, Т=550 К;
77. Гелий m1=3 г и азот m2=30 г, Т=700 К;
78. Углекислый газ m1=25 г и азот m2=32 г, Т=650 К;
79. Углекислый газ m1=31 г и водород m2=3 г, Т=420 К;
80. Углекислый газ m1=7 г и гелий m2=4 г, Т=720 К.
81. Азот, находившийся в состоянии 1 с параметрами 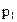 =0,2 МПа,
=0,2 МПа,  =450 К,
=450 К,  =2л, изотермически перевели в состояние 2 с объемом
=2л, изотермически перевели в состояние 2 с объемом  =6 л. Затем адиабатно объем газа был увеличен до
=6 л. Затем адиабатно объем газа был увеличен до  =9 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=9 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
82. Гелий, находящийся в состоянии 1 при давлении 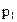 =0,25 МПа, температуре
=0,25 МПа, температуре  =550 К и занимающий объем
=550 К и занимающий объем  =2,5л, изобарно перевели в состояние 2 с температурой Т2=650 К. Затем адиабатно объем газа был увеличен на 3 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=2,5л, изобарно перевели в состояние 2 с температурой Т2=650 К. Затем адиабатно объем газа был увеличен на 3 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
83. Кислород, находящийся в состоянии 1 при давлении 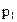 =0,25 МПа, температуре
=0,25 МПа, температуре  =550 К и занимающий объем
=550 К и занимающий объем  =2,5л, изохорно перевели в состояние 2 с температурой Т2=650 К. Затем адиабатно давление газа было уменьшено в 2 раза. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=2,5л, изохорно перевели в состояние 2 с температурой Т2=650 К. Затем адиабатно давление газа было уменьшено в 2 раза. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
84. Водород, находящийся в состоянии 1 ( 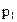 =0,1 МПа,
=0,1 МПа,  =300 К,
=300 К,  =1л), перевели в состояние 2, адиабатно уменьшив давление на 20%. Затем изобарно объем газа был увеличен до
=1л), перевели в состояние 2, адиабатно уменьшив давление на 20%. Затем изобарно объем газа был увеличен до  =2 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=2 л. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
85. Гелий, находящийся в состоянии 1 ( 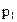 =310 кПа,
=310 кПа,  =400 К,
=400 К,  =10л), перевели в состояние 2, адиабатно увеличив давление в два раза. Затем изотермически объем газа был увеличен на 6 литров. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=10л), перевели в состояние 2, адиабатно увеличив давление в два раза. Затем изотермически объем газа был увеличен на 6 литров. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
86. Кислород, находящийся в состоянии 1 ( 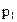 =230 кПа,
=230 кПа,  =450 К,
=450 К,  = 20л), перевели в состояние 2, адиабатно уменьшив объем в три раза. Затем изохорно температура газа была увеличена на 100 К. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
= 20л), перевели в состояние 2, адиабатно уменьшив объем в три раза. Затем изохорно температура газа была увеличена на 100 К. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
87. Кислород, находящийся в состоянии 1 при давлении 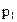 =250 кПа, температуре
=250 кПа, температуре  =550 К и занимающий объем
=550 К и занимающий объем  =12л, изотермически перевели в состояние 2 с объемом
=12л, изотермически перевели в состояние 2 с объемом  =6 л. Затем адиабатно объем газа был уменьшен на два литра. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=6 л. Затем адиабатно объем газа был уменьшен на два литра. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
88. Азот, находящийся в состоянии 1 при давлении 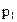 =220 кПа, температуре
=220 кПа, температуре  =430 К и занимающий объем
=430 К и занимающий объем  =25л, изобарно перевели в состояние 2, уменьшив объем на семь литров. Затем адиабатно давление газа было уменьшено на 30%. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=25л, изобарно перевели в состояние 2, уменьшив объем на семь литров. Затем адиабатно давление газа было уменьшено на 30%. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
89. Гелий, находящийся в состоянии 1 при давлении 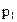 =150 кПа, температуре
=150 кПа, температуре  =500 К и занимающий объем
=500 К и занимающий объем  =12,5л, изотермически перевели в состояние 2 с объемом 6,5 литра. Затем адиабатно температура газа была уменьшена на 100 К. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=12,5л, изотермически перевели в состояние 2 с объемом 6,5 литра. Затем адиабатно температура газа была уменьшена на 100 К. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
90. Водород, находящийся в состоянии 1 при давлении 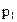 =0,25 МПа, температуре
=0,25 МПа, температуре  =550 К и занимающий объем
=550 К и занимающий объем  =2,5л, изохорно перевели в состояние 2 с давлением р2=0,5 МПа. Затем адиабатно объем газа был увеличен в 1,5 раза. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
=2,5л, изохорно перевели в состояние 2 с давлением р2=0,5 МПа. Затем адиабатно объем газа был увеличен в 1,5 раза. Определить термодинамические параметры каждого из состояний. Для каждого из описанных процессов найти: 1) работу, совершенную газом; 2) изменение его внутренней энергии; 3) количество подведенной к газу теплоты.
91. Определить изменение энтропии 14 г азота при изобарном нагревании его от 270С до 1270С.
92. Как изменится энтропия 2 молей углекислого газа при изотермическом расширении, если объем газа увеличился в четыре раза?
93. Найти изменение энтропии при нагревании 2 кг воды от 0 до 1000С и последующем превращении ее в пар при той же температуре. Удельная теплоемкость воды – 4190 Дж/кг К, удельная теплота парообразования -  Дж/кг.
Дж/кг.
94. Определить изменение энтропии при затвердевании 2 кг свинца и дальнейшем его охлаждении от 327 до 00С. Удельная теплота плавления свинца – 0,25  Дж/кг, удельная теплоемкость свинца – 120 Дж/кг К.
Дж/кг, удельная теплоемкость свинца – 120 Дж/кг К.
95. Определить изменение энтропии при плавлении 1 кг льда, находившегося при температуре 00С, и последующем нагревании воды до температуры 570С.. Удельная теплота плавления льда – 3,35  Дж/кг, удельная теплоемкость воды – 4190 Дж/кг К
Дж/кг, удельная теплоемкость воды – 4190 Дж/кг К
96. В результате изохорного нагревания водорода массой 1 г давление газа увеличилось в два раза. Определить изменение энтропии газа.
97. Найти изменение энтропии при изобарном расширении азота массой 4 г от объема V1=5 л до объема V2=9 л.
98. Объем кислорода массой 1 кг был увеличен в 5 раз в результате изотермического расширения. Найти изменение энтропии газа.
99. Объем кислорода массой 2 кг был увеличен в 5 раз в результате адиабатного расширения. Найти изменение энтропии газа.
100. Во сколько раз необходимо увеличить объем 10 г водорода, чтобы при изотермическом расширении его энтропия увеличилась на 57,6 Дж/К?
1) Баллистический маятник – массивное тело, подвешенное на тонких нерастяжимых нитях длиной L.
Дата добавления: 2015-02-10; просмотров: 401; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Основные типы циклов | | | Электрооборудование автомобиля |