Вложенные условные операторы

Следует помнить, что синтаксис языка допускает запись только одного оператора после ключевых слов then и else, поэтому группу инструкций обязательно надо объединить в составной оператор. Составной оператор – это заключенная между зарезервированными словами begin (НАЧАЛО) и end (КОНЕЦ) последовательность операторов, отделенных друг от друга точкой с запятой:

begin

<Оператор 1>;

<Оператор 2>;

…

<Оператор N>

End

Каждый оператор, входящий в составной, может быть простым или структурным. Структурные операторы, в свою очередь, могут содержать составные. Зарезервированные слова begin и end называются операторными скобками.

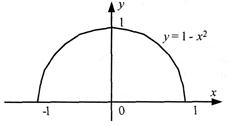
Рис. 4. График функции

Примером простейшего разветвляющегося вычислительного процесса может служить программа определения значения функции у = f(x) (рис. 4).

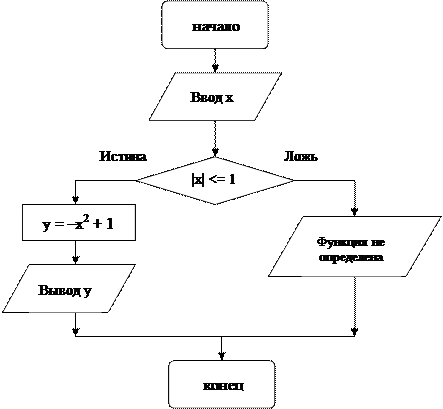
Рис. 5. Схема разветвляющегося алгоритма

Так как функция определена на отрезке [–1; 1], то при ее вычислении необходимо использовать структуру выбора, в одной ветви которой вычисляется значение по формуле у = –х² + 1 и выводится на экран, а в другой – выводится сообщение ФУНКЦИЯ НЕ ОПРЕДЕЛЕНА. Алгоритм решения задачи представлен на рис. 5. Ниже приведен текст программы.

Program Razvilka;

{Описание переменных: x – значение аргумента; у – значение функции}

Var x, y: real;

Begin

Writeln ('Введите значение x');

Readln (x);

{Вычисление значения функции}

If abs(x) <= 1

Then

begin у := –x*x+1; Writeln ('y=', y:6:3); end

elseWrite ('Функция не определена');

Readln;

End.

Рассмотрим ещё один пример. Дано действительное число х. Вычислить значение функции f(х), если

f(x)=

Алгоритм в данном случае имеет вложенную ветвящуюся структуру.

Program Formula;

Var x, f: real;

Begin

Writeln ('Введите значение действительного числа x');

Readln (x);

If (x <= 0)

thenf := 0

else If (x <= 1) thenf := sqr(x) – x

elsef := sqr(x) – sin(Pi*x*x);

Write ('Значение функции F(x) при x=', x,' равно', f:8:3);

End.

Таким образом, структура выбора может входить составной частью в одну из ветвей другой структуры выбора. В этом случае имеет место сложное разветвление. Тогда ветвь else всегда относится к ближайшему if, не имеющему else. Примером задачи, также приводящей к сложному разветвлению, может служить следующая задача: из трех данных вещественных чисел X, Y, Z выбрать наибольшее(рис.6).

Рис. 6. Схема алгоритма сложного ветвления

{Использование алгоритма с вложенными полными ветвлениями}

Program MAX_1;

Var x, y, z: real;

Begin

Writeln ('Введите через пробел значения x, y, z');

Readln (x, y, z);

If x >= y

then ifx >= z thenmax := x elsemax := z;

else ify >= z thenmax := y elsemax := z;

Writeln (‘Максимальное значение =’, max:8:2);

End.

Этот же пример можно решить, используя алгоритм с последовательными неполными ветвлениями и сложными логическими выражениями.

Program MAX_2;

{Описание переменных: x, y, z – действительные числа}

Var x, y, z: real;

Begin

Writeln ('Введите через пробел значения x, y, z');

Readln (x, y, z);

If (x >= y) and (x >= z) thenmax := x;

If (y >= z) and (y >= z) thenmax := y;

If(z >= x) and (z >= y) then max := z;

Writeln (‘Максимальное значение =', max:8:2);

End.