
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определенный интеграл
Справочный материал
 1. Пусть функция y=f(x) определена на отрезке [a;b]. Разобьем произвольным образом этот отрезок точками a=x0<x1<x2<…<xn=b на n частичных отрезков длиной Δxi=xi-xi-1, i=1, n. Выберем в каждом из них точку сi. Сумма вида
1. Пусть функция y=f(x) определена на отрезке [a;b]. Разобьем произвольным образом этот отрезок точками a=x0<x1<x2<…<xn=b на n частичных отрезков длиной Δxi=xi-xi-1, i=1, n. Выберем в каждом из них точку сi. Сумма вида
 (1)
(1)
называется интегральной суммой функции y=f(x) на отрезке [a;b].
Определенным интегралом от функции f(x) на отрезке [a;b] называют предел интегральной суммы (1)при условии, что длина наибольшего частичного отрезка Δxi стремится к нулю:
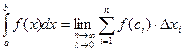 (2)
(2)
f(x) – подынтегральная функция
[a; b] – отрезок интегрирования
a и b – нижний и верхний пределы интегрирования
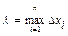 - длина наибольшего частичного отрезка.
- длина наибольшего частичного отрезка.
Геометрический смысл определенного интеграла: Если f(x)≥0 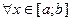 , то определенный интеграл от непрерывной функции y=f(x) равен площади криволинейной трапеции, заключенной под графиком функции y=f(x) на отрезке [a; b]:
, то определенный интеграл от непрерывной функции y=f(x) равен площади криволинейной трапеции, заключенной под графиком функции y=f(x) на отрезке [a; b]:
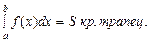 (3)
(3)
2. Свойства определенного интеграла:
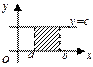 1°
1° 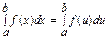 - определенный интеграл не зависит от обозначения переменной;
- определенный интеграл не зависит от обозначения переменной;
2° 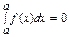 3°
3° 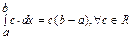
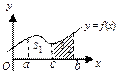 |
4° 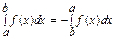 5°
5° 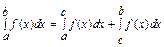
6° 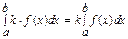 7°
7° 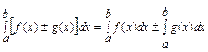
8° Если f(x) ≤ g(x),  то
то
 - (неравенство между непрерывными функциями можно интегрировать).
- (неравенство между непрерывными функциями можно интегрировать).
9° Если m, M – наименьшее и наибольшее значения функции f(x) на [a; b], то
 - оценка интеграла.
- оценка интеграла.
10° Теорема о среднем. Если функция y=f(x) непрерывна на [a; b], то  :
:
|
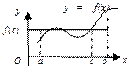
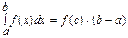
3. Формула Ньютона – Лейбница.Если F(x) – какая-нибудь первообразная функции f(x), то
 (4)
(4)
т.е. определенный интеграл равен приращению первообразной на отрезке интегрирования.
Дата добавления: 2015-04-11; просмотров: 202; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Вирусные энтомопатогенные препараты | | | Пән бойынша тесттік тапсырмалар |