
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
LIBRARY ieee;
Операция деления без восстановления остатка над целыми двоичными числами со знаком, представленными в дополнительном коде
3.2.1. Алгоритм деления 2n : n
Напомним реализацию операции деления на ассемблере i8086 для целых двоичных чисел со знаком, представленных в дополнительном коде словарной длины.
При выполнении этой операции используются две команды CWD (команда знакового расширения слова до двойной длины) и IDIV(собственно команда деления) в следующей последовательности:
Cwd;
idiv word ptr [r/m]; где word ptr [r/m] определяет адрес источника
; (r – регистр / m – ячейка памяти), где хранится 16-разрядный делитель.
Для того, чтобы разработать алгоритм микропрограммной реализации указанных действий приведем краткое словесное описание этих команд
Команда CWD обеспечивает преобразование слова в двойное слово
| Код операции | Команда | Число тактовых циклов | Описание | |
| CWD | DX <- расширение знаком AX | |||
| Начиная с i80386 команда cwd заменена на команду cmde: | ||||
| CWDE | 3(i486) | EAX<- расширение знаком AX |
Правила выполнения команды cwd
DX <− SignExtend(AX) (расширением знаком);
Описание
Команда CWD преобразовывает имеющее знак в регистре AX слово в имеющее знак двойное слово в регистрах DX:AX путем расширения старшего бита регистра AX (бита знака) на два байта регистра DX.
Команда IDIV − Деление со знаком
| Код операции | Команда | Число тактовых циклов | Описание | |
| F7 /7 | IDIV r/m16 | 27/28 (i486) | Деление со знаком DX:AX на слово из [r/m] (результат: AX=частное, DX = остаток) |
Правила выполнения команды рассмотрены ниже
врем <− делимое / делитель;
IF врем не помещается в частном
THEN Прерывание 0;
ELSE
частное <− врем;
остаток <− делимое .mod. (r/m); операция взятия остатка от деления
END IF;
Замечание: Делитель задается явно в ячейке с адресом r/m (регистр/память). Делимое, частное и остаток используют неявно задаваемые регистры AX, DX, соответственно. Числа представляются в дополнительном коде со знаком.
Если полученное частное слишком велико и не может поместиться в операнде назначения, или делитель предварительно был равен 0 ( деление на 0), то генерируется прерывание 0 (int0).
Нецелые частные усекаются до 0. Остаток имеет тот же знак, что и делимое, а его абсолютное значение всегда меньше абсолютного значения делителя.
Например: при делении -5 на +6 получим в частном 0, а в остатке -5, при делении +6 на -5 получим в частном -1, а в остатке +1.
Флаги результата OF, SF, ZF, AF, PF, CF не определены.
Проанализировав приведенное выше краткое справочное описание правил выполнения команд можно сделать предположение, что для реализации команды IDIV использован классический алгоритм деления без восстановления остатка, подробно разобранный, например, в [Каган Б.М. Электронные вычислительные машины и системы. - М.: Энергоатомиздат , 1985.- 552 с. : ил.; Пьявченко О.Н. Алгоритмические основы выполнения математических операций в микрокомпьютерах: Учебное пособие. − Таганрог: Изд-во ТРТУ, 1998. 190 с.].
Именно этот алгоритм работает над двумя N-разрядными целыми двоичными числами, представленными в дополнительном коде, причем первое из них (делимое) предварительно должно быть расширено по знаку до 2N-разрядного целого двоичного числа. Алгоритм регулярен по числу шагов основного цикла и имеет в процессе завершения два шага коррекции, правила выполнения которых зависит от сочетания знаков делимого, делителя и полученного в основном цикле ненулевого остатка, что будет подробно рассмотрено ниже.
Введем условные обозначения:
ДМ - n-разрядная регистровая ячейка для размещения кода делимого,
ДТ - n-разрядная регистровая ячейка для размещения кода делителя,
ЧОСТ - n-разрядная регистровая ячейка для размещения кода частичного остатка,
ОСТ - n-разрядная регистровая ячейка для размещения кода результирующего остатка,
ЧАСТН - n-разрядная регистровая ячейка для размещения кода частного результата,
ТСРЗН – одноразрядная ячейка (триггер) сравнения знаков делимого (затем ЧОСТ) и делителя: если знаки равны, то ячейка содержит 1, иначе - 0,
ТСРЗНдоп – дополнительная одноразрядная ячейка (триггер) сравнения знаков делимого и делителя: если знаки равны, то ячейка содержит 1, иначе - 0,
КОРР1 – первый шаг коррекции,
КОРР2 – второй шаг коррекции,
ЗНДМ – знак делимого,
ЗНДТ – знак делителя,
ЗНЧОСТ – знак частичного остатка,
NOT – битовая операция логического отрицания.
SIGN(ДМ) – операция размножения знака делимого до слова длиной N двоичных разрядов.
Ниже приведем словесное описание алгоритма выполнения операции деления без восстановления остатка над N-разрядными двоичными целыми числами со знаком, представленными в дополнительном коде.
1. Проверить делимое ДМ на равенство нулю. Если да, то завершить выполнение операции, поместив в регистры результата числовое значение беззнакового нуля.
2. Проверить делитель ДТ на равенство нулю. Если да, то завершить выполнение операции с ошибкой деления на ноль.
3. Размножить знак ДМ в регистровую ячейку ЧОСТ, а также установить значения ячеек ЗНДМ и ЗНДТ.
4. Сформировать значение в ТСРЗН, ТСРЗНдоп, равные NOT(ЗНДМ Å ЗНДТ).
5. (Начало основного цикла) Выполнить логический сдвиг влево на один разряд значений регистров ЧОСТ, ДМ. Причем в освободившийся младший разряд ЧОСТ[0] занести вытолкнутое значение старшего разряда ДМ[N-1], а значение младшего разряда ДМ[0] установить равным ТСРЗН.
6. Проверить ТСРЗН: если ячейка равна 1, то перейти к п.7, иначе (при 0) перейти к п.8.
7. Выполнить операцию вычитания из ЧОСТ значения ДТ: ЧОСТ:= ЧОСТ – ДТ и перейти к п.9.
8. Выполнить операцию приращения ЧОСТ на значение ДТ: ЧОСТ:= ЧОСТ + ДТ и перейти к п.9.
9. Сформировать значение в ТСРЗН, равное NOT ( ЗНЧОСТÅ ЗНДТ ).
10. N-раз повторить п.п. 5-9, где N-разрядность числа, включая его знак.
11. ((N+1) – й шаг алгоритма. Начало шага.) Выполнить логический сдвиг влево на один разряд значения регистра ДМ. Причем освободившееся значение младшего разряда ДМ[0] установить равным ТСРЗН. Вытолкнутое значение старшего разряда регистра ДМ теряется.
12. Перегрузить регистр ДМ в регистр ЧАСТН. Проверить ЧОСТ на равенство 0: если да, то не выполнять коррекцию частичного остатка и перейти к п.22, иначе выполнить п.13.
13. Проверить ТСРЗН: если ячейка равна 1 , то перейти к п.14, иначе (при 0) перейти к п.15.
14. Выполнить операцию вычитания из ЧОСТ значения ДТ: ЧОСТ:= ЧОСТ – ДТ и перейти к п.16.
15. Выполнить операцию приращения ЧОСТ на значение ДТ: ЧОСТ:= ЧОСТ + ДТ и перейти к п.16.
16. (Конец N+1-го шага алгоритма) Сформировать значение в ТСРЗН, равное NOT(ЗНЧОСТ Å ЗНДТ).
17. Проверить ЧОСТ на равенство 0: если да, то перейти к п.22, иначе – перейти к п.18.
18. Сравнить знак ЧОСТ со знаком делимого в исходном представлении (ЗНДМ): Если знаки равны, то перейти к п.22 (шаг КОРР1 не нужен), иначе перейти к п.19.
Структура первого шага коррекции Таблица 3.5
| Знак ДМ | ЗнакЧОСТ | Знак ДТ | КОРР1 | Комментарий |
| + | + | Любой | Нет | Коррекция не нужна |
| - | - | Любой | Нет | Коррекция не нужна |
| + | - | + | + ДТ | К ЧОСТ прибавить ДТ |
| - | - ДТ | От ЧОСТ вычесть ДТ | ||
| - | + | + | - ДТ | От ЧОСТ вычесть ДТ |
| - | + ДТ | К ЧОСТ прибавить ДТ |
19. Выполнить шаг КОРР1 (см. таблицу 3.5): восстановить остаток. Для чего проверить значение ТСРЗН: если триггер равен 1 (знаки ЧОСТ и ДТ равны), то п.20, иначе п.21.
20. Выполнить операцию вычитания из ЧОСТ значения ДТ: ЧОСТ:= ЧОСТ – ДТ и перейти к п.22.
21. Выполнить операцию приращения ЧОСТ на значение ДТ: ЧОСТ:= ЧОСТ + ДТ и перейти к п.22.
22. Выполнить здесь и далее второй шаг коррекции (КОРР2). Для чего проверить исходные знаки ДМ и ДТ (см. таблицу 3.6): если ТСРЗНдоп равняется 1 (знаки ДМ и ДТ равны), то п.23, иначе (при неравенстве знаков ДМ и ДТ) перейти к п.26.
Таблица 3.6
Структура второго шага коррекции
| Знак ДМ | Знак ДТ | ЧОСТ | КОРР2 | Комментарий |
| + | + | Любой | Нет | Коррекция не нужна |
| + | - | Любой | +1 | Нарастить ЧАСТН на 1 |
| - | + | ≠ 0 | +1 | Нарастить ЧАСТН на 1 |
| = 0 | Нет | Коррекция не нужна | ||
| - | - | ≠ 0 | Нет | Коррекция не нужна |
| = 0 | +1 | Нарастить ЧАСТН на 1 |
23. Проверить исходный знак ДМ: если ЗНДМ равняется 0 (ДМ положительно), то коррекция ЧАСТН не нужна и переход к п.28, иначе п.24.
24. Проверить значение ЧОСТ на равенство 0, если ЧОСТ не равен 0, то коррекция ЧАСТН не нужна и перейти к п.28, иначе п. 25.
25. Нарастить частное на 1: ЧАСТН := ЧАСТН +1, перейти к п.28.
26. Проверить исходный знак ДМ: если ЗНДМ равняется 0 (ДМ положительно), то переход к п.25, иначе п.27.
27. Проверить значение ЧОСТ на равенство 0, если ЧОСТ равен 0, то коррекция не нужна и перейти к п.28, иначе п. 25.
28. Регистр ОСТ загрузить содержимым ЧОСТ и завершить алгоритм.
29. Конец алгоритма.
3.2.2. Числовые примеры реализации операции деления
Поясним работу алгоритма на нескольких числовых примерах.
Пример 3.4
Пусть необходимо поделить два числа 7 и -5.
Представим эти десятичные числа в форме четырех разрядного дополнительного двоичного кода: ДМ - 01112 и ДТ - 10112, соответственно. Величина (–ДТ) равна 0101. Тогда имеют место следующие действия
Таблица 3.7
| Nо шага | Операция | ЧОСТ | ДМ | ТСРЗН ДТ = 1011 | ТСРЗНдоп | ЧАСТН | ОСТ | Комментарии |
| Загрузка ЧОСТ, ДМ, ТСРЗН… | ||||||||
| Сдвиг влево | ||||||||
| +ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +(-ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +(-ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +(-ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево только над ДМ | ||||||||
| +ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| +(-ДТ) | КОРР1 | |||||||
| ОСТ найден | ||||||||
| +1 | КОРР2: ЧАСТН +=1 , т.к. ДМ>0 и ДТ<0 | |||||||
| Найден полный результат |
Пример 3.5
Пусть необходимо поделить два числа -7 и +5.
Представим эти десятичные числа в форме четырех разрядного дополнительного двоичного кода: ДМ - 10012 и ДТ - 01012, соответственно. Величина
(–ДТ) равна 10112.
Тогда имеют место следующие действия
Таблица 3.8
| Nо шага | Операция | ЧОСТ | ДМ | ТСРЗН ДТ = 0101 | ТСРЗНдоп | ЧАСТН | ОСТ | Комментарии |
| Загрузка ЧОСТ, ДМ, ТСРЗН… | ||||||||
| Сдвиг влево | ||||||||
| +ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +(-ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +(-ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +(-ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево только над ДМ | ||||||||
| +ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| +(-ДТ) | КОРР1 | |||||||
| ОСТ найден | ||||||||
| +1 | КОРР2: ЧАСТН +=1, т.к. ОСТ <> 0 и ДМ<0 и ДТ>0 | |||||||
| Найден полный результат |
Пример 3.6
Пусть необходимо поделить два числа -7 и -5.
Представим эти десятичные числа в форме четырех разрядного дополнительного двоичного кода: ДМ - 10012 и ДТ - 10112, соответственно. Величина (–ДТ) равна 01012.
Тогда имеют место следующие действия
Таблица 3.9
| Nо шага | Операция | ЧОСТ | ДМ | ТСРЗН ДТ = 1011 | ТСРЗНдоп | ЧАСТН | ОСТ | Комментарии |
| Загрузка ЧОСТ, ДМ, ТСРЗН… | ||||||||
| Сдвиг влево | ||||||||
| +(–ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| + ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево только над ДМ | ||||||||
| +(–ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| +ДТ | КОРР1 | |||||||
| ОСТ найден | ||||||||
| +0 | Нет КОРР2, т.к. ОСТ <> 0 и ДМ<0 и ДТ<0 | |||||||
| Найден полный результат |
Пример 3.7
Пусть необходимо поделить два числа -6 и +2.
Представим эти десятичные числа в форме четырех разрядного дополнительного двоичного кода: ДМ - 10102 и ДТ - 00102, соответственно. Величина (–ДТ) равна 11102.
Тогда имеют место следующие действия
Таблица 3.10
| Nо шага | Операция | ЧОСТ | ДМ | ТСРЗН ДТ = 1011 | ТСРЗНдоп | ЧАСТН | ОСТ | Комментарии |
| Загрузка ЧОСТ, ДМ, ТСРЗН… | ||||||||
| Сдвиг влево | ||||||||
| +ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +(-ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +(-ДТ) | ЧОСТ -=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево | ||||||||
| +ДТ | ЧОСТ +=ДТ | |||||||
| Результат суммы | ||||||||
| Сдвиг влево только над ДМ | ||||||||
| +0 | Нет суммирования, т.к. ЧОСТ = 0 | |||||||
| Результат суммы | ||||||||
| +0 | Нет КОРР1, т.к. ЧОСТ = 0 | |||||||
| ОСТ найден | ||||||||
| +0 | Нет КОРР2, т.к. ОСТ = 0 и ДМ<0 и ДТ>0 | |||||||
| Найден полный результат |
3.2.3. Разработка операторной граф-схемы алгоритма реализации операции деления на учебном микропрограммируемом микропроцессоре.
Предварительно распределим регистры микропроцессора, объявленные в описании лабораторной работы №1. Регистр R3 загрузим значением дополнительного кода ДТ. Регистры R1 и RQ загрузим значением дополнительного кода ДМ, кроме того, RQ затем будем использовать для формирования разрядов частного. Регистр R2 загрузим значением знака ДМ. Регистр R8 будем использовать как «сдвиговый регистр-счетчик» с начальным значением 1: отсчет количества циклов будем вести по старшему знаковому разряду. Результат будем возвращать в регистры R2 (остаток) и R0(частное).
Введем остальные обозначения.
Оператор сдвига одинарной длины влево на один разряд над регистром R8 , при котором выталкиваемое значение старшего разряда регистра R8[n-1] теряется, а в освободившийся младший разряд R8[0] заносится 0, обозначим как R8 :=ЛевОдинЛог(R8+0).0; где R8+0 – сумма значения восьмого регистра с нулем.
Оператор сдвига двойной длины влево на один разряд над регистрами R2 и RQ, при котором выталкиваемое значение старшего разряда регистра RQ[n-1] заталкивается в младший разряд регистра R2[0], а в освободившийся разряд регистра RQ[0] заносится 0, обозначим как
(R2,RQ) :=ЛевДвЛог((R2+0),RQ).0;
где R2+0 – сумма значения второго регистра с нулем.
F – выход комбинационного АЛУ из состава микропроцессора.
FZ – флаг значения признака равенства нулю результата F на выходе АЛУ микропроцессора: при FZ = 1 результат равен 0.
FN– флаг значения признака знака результата F на выходе АЛУ микропроцессора: при FN = 1 результат меньше 0.
FErrorDiv - флаг значения признака ошибки деления: если FErrorDiv не равен 0, то это свидетельствует об осуществлении попытки деления на ноль или переполнении разрядной сетки частного.
Замечание. Установка флагов производится в конце текущего такта работы микропроцессора по результату выполнения в нем текущей микрооперации. Поэтому ветвление по этим признакам можно осуществлять только на следующем такте (не ранее).
Приняв указанные обозначения, выполним их подстановку в рассмотренный выше словесный алгоритм деления, а затем переведем данный алгоритм на язык операторных граф-схем алгоритмов с учетом возможностей учебного микропрограммируемого микропроцессора (см. описание лабораторной работы №1). Операторная граф-схема алгоритма реализации операции деления, полученная таким образом, приведена рисунках 3.10, 3.11, 3.12, 3.13.
Ниже в таблице 3.10 приведем фрагмент двоичного кода микропрограммы деления для соответствующих операторных и условных вершин из состава основного цикла приведенной граф-схемы алгоритма.
Тот же фрагмент алгоритма, закодированный средствами программной модели учебного микропрограммируемого микропроцессора, представлен на рис. 3.14.
Таблица 3.10
Структура фрагмента микропрограммы (основной цикл)
| Aдрес | ВR50 | P30 | М20 | I86 | I20 | Сin | Aim | I53 | АЗ0 | В30 | D70 |
| 011*) | |||||||||||
*) - в модели учебного микропроцессора операция двойного сдвига ЛевДвЛог(…) обозначена как Л_ДвАр_(…), т.е. как арифметический, однако выполняется как и в большинстве микропроцессоров, как логический сдвиг с занесением 0 в младший разряд младшего регистра в паре.

Рис. 3.14 – Фрагмент микропрограммы, реализующий основной цикл операции целочисленного деления без восстановления остатка
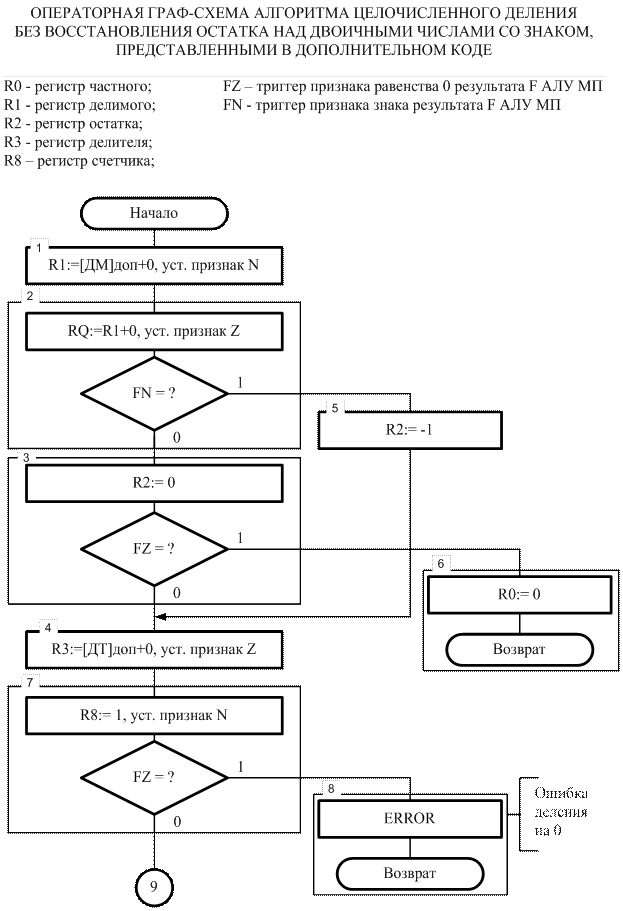
Рис. 3.10. Операторная граф-схема алгоритма деления
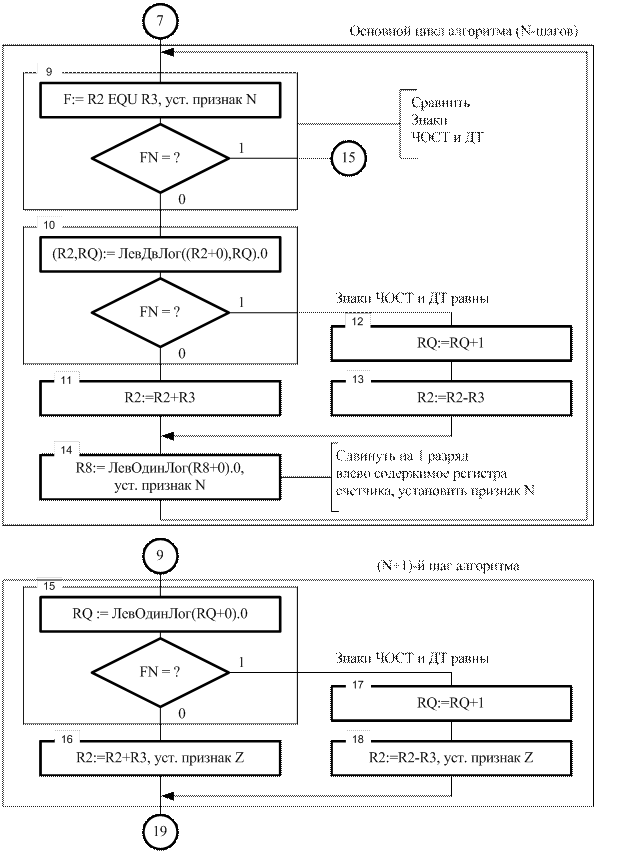
Рис. 3.11. Операторная граф-схема алгоритма деления. Продолжение
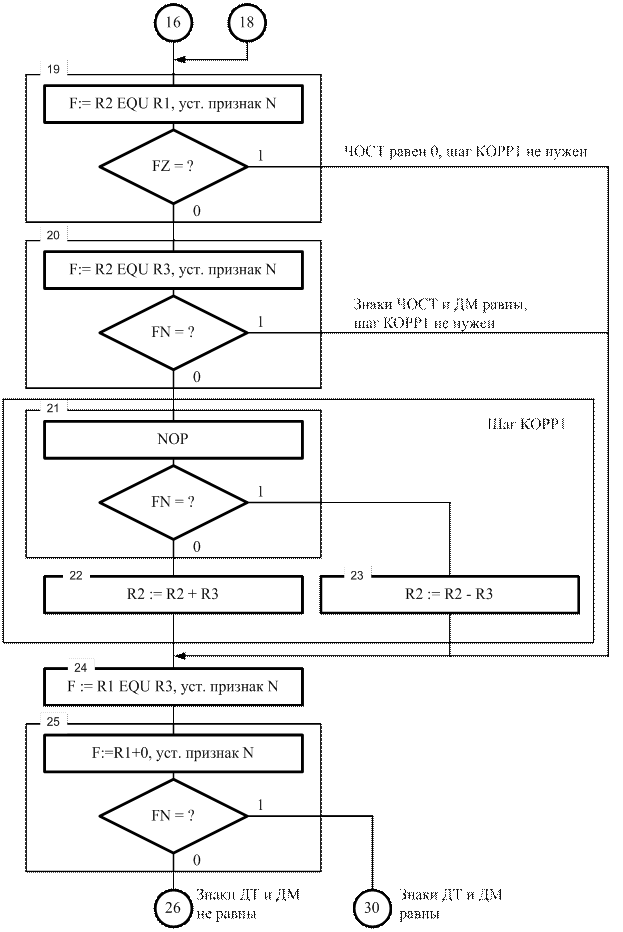
Рис. 3.12. Операторная граф-схема алгоритма деления. Продолжение

Рис. 3.13. Операторная граф-схема алгоритма деления. Окончание
Приведенный выше алгоритм деления без восстановления остатка был реализован на языке VHDL (см. приложение). Процессная модель операции деления, поясняющая его работу, приведена на рис. 3.15.
Основные обозначения:
SDM – знак ДМ.
SDT – знак ДТ.
INT15 – чистовая константа, равная 15.
CH_OST – регистр частичного остатка (ЧОСТ).
ZCH_OST – выход мультиплексора формирования частичного остатка, установленный на входе регистра CH_OST.
R_OST – регистр остатка.
DM – регистр ДМ.
DT – регистр ДТ.
ZF - признак CH_OST=0.
ZZF- признак R_OST=0.
SS <= NOT (DA(INT15) XOR DB(INT15)); --- признак равенства знаков ДМ и ДТ.
SN <= NOT (SDT XOR ZCH_OST(INT15)); --- признак равенства знаков ДТ и ЧОСТ.
VF <= SDM XOR CH_OST(INT15); --- признак неравенства знаков ДМ и ЧОСТ.
FF <= NOT (SDM XOR SDT); -- признак равенства знаков ДМ и ДТ.
SHIFT – шаги основного цикла алгоритма.
LAST – (n +1) – й шаг алгоритма.
LAST2 –первый шаг коррекции КОРР1.
LAST3 –второй шаг коррекции КОРР2.
START – сигнал запуска машины состояния операции деления (запуск процессов вычисления операции).
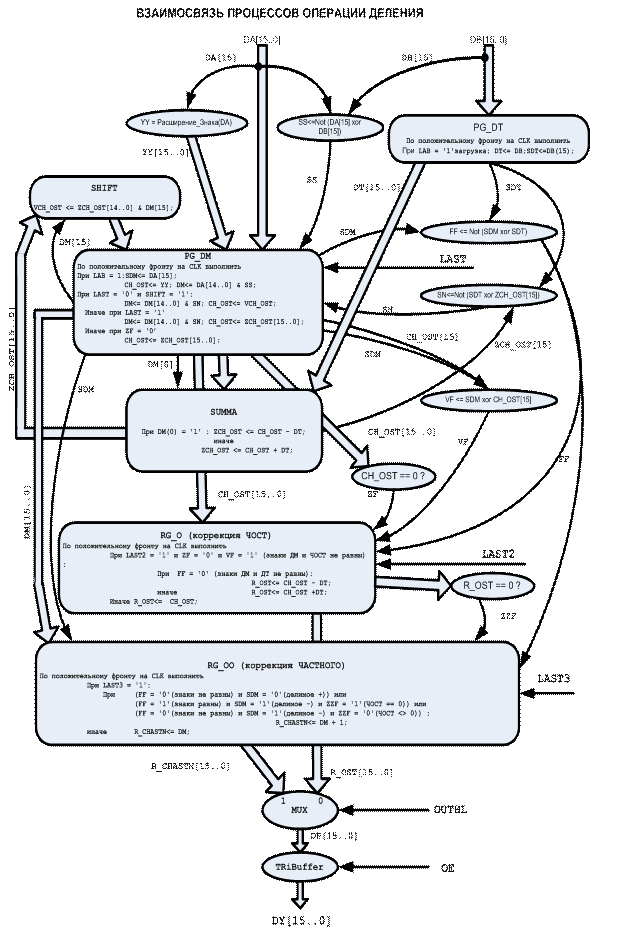 Рис. 3.15. Процессная модель операции деления (откорректированная)
Рис. 3.15. Процессная модель операции деления (откорректированная)
На остальных рисунках – 3.16, 3.17 и 3.18 представлены результаты выполненных в среде QuartusII экспериментов.
Структура блока деления двух чисел представлена на рис. 3.16. Из структуры видно, что запуск блока производится по сигналу START . Данные по шинам DA, DB необходимо подавать в момент выдачи блоком сигнала LAB. При этом подаваемые на шины числовые значения должны быть синхронизированы с CLK (т.е. охватывать положительный фронт тактирующих импульсов). Установка сигнала RDY в состояние логической единицы говорит о завершении блоком требуемых вычислений. Сигнал ОЕ =1 позволяет подключить выход устройства к шине результата DY. Причем при OUTHL = 1 на шину DY будет выдано рассчитанное частное, а при OUTHL = 0 – остаток. Очевидно, что указанные значения будут действительны только при RDY = 1.
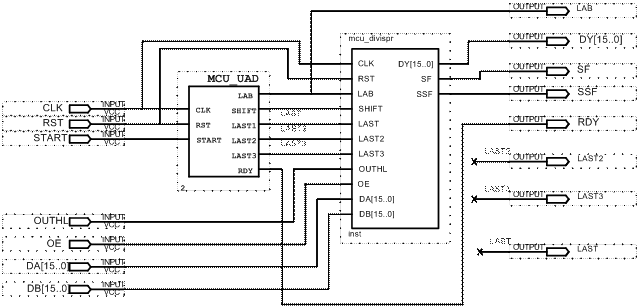
Рис. 3.16 – Структура блока деления
На рис. 3.17 приведена временная диаграмма работы операционного автомата деления числа А (шина DA) на число B(шина DB) , где A и B – числа целые со знаком, представленные в дополнительном коде. Здесь отражены такие основные процессы функционирования устройства как загрузка числовых данных по сигналу LAB (числа -3675 и 600), выполнение по тактам основного цикла алгоритма, сопровождаемого сигналом SHIFT, а также процессы коррекции результата LAST2, LAST3 и формирования конечного результата на информационной выходной шине DY (частное – -6 (или FFFAh), остаток –
-75(или FFB5h )).
Особенности функционирования блока деления в целом представлены на рисунке 3.18.

Рис. 3.16 – Временная диаграмма работы операционной части блока деления
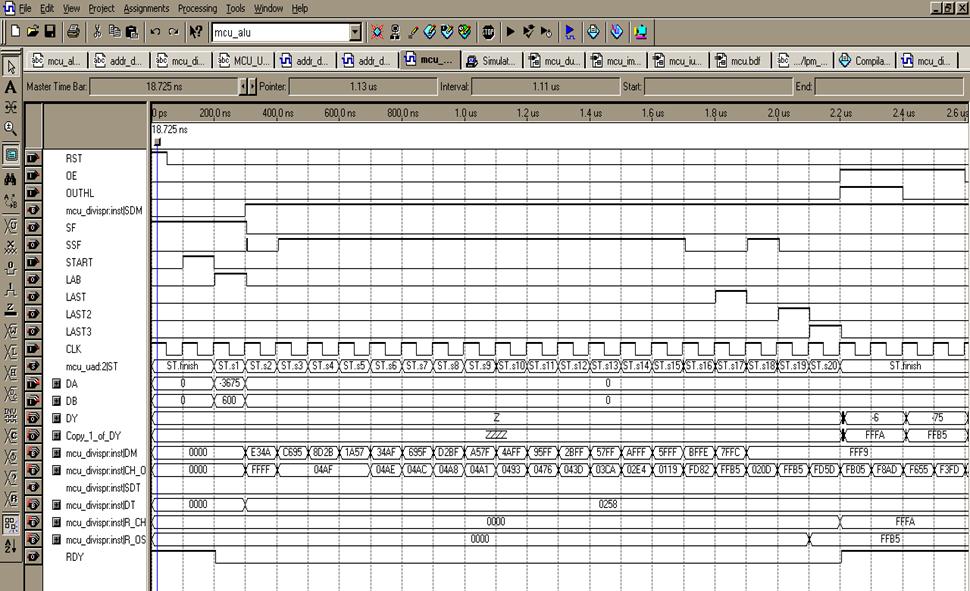
Рис. 3.18. Временная диаграмма работы блока деления в сборе
ПРИЛОЖЕНИЕ П1 Реализация операции «Деление»
------------- Пакет описания типов
LIBRARY ieee;
Дата добавления: 2015-04-11; просмотров: 276; Мы поможем в написании вашей работы!; Нарушение авторских прав |