Прямой алгоритм вычисления CRC: применение и недостатки.

К примеру, вычисление по этому алгоритму CRC для исходной последовательности 1101001110010110100 (см. рис. 9.4) и сама окончательная последовательность на стороне источника будут выглядеть так, как показано на рис. 9.5.
Из рисунка видно, что в начале вычисления исходная последовательность 1101001110010110100 дополняется нулями в количестве, равном степени полинома (Р=1011 - степень полинома N=3): 1101001110010110100+000. При выполнении CRC-деления эти дополнительные биты гарантируют, что все биты исходной последовательности примут участие в процессе формирования значения CRC. Результирующая последовательность получается равной исходной последовательности, дополненной значением CRC: 1101001110010110100+011. Заметим, что длина присоединяемого к исходной последовательности значения CRC должна быть равна степени полинома, даже если CRC, как в нашем случае, имеет ведущие нули. Это очень важный момент, понимание которого является ключом к пониманию сути процессов, происходящих на стороне приемника при получении и определении целостности исходного сообщения. Действия алгоритма для приемника просты — выполнить деление полученной последовательности на полином. При этом для выполнения деления нет необходимости дополнять исходную последовательность нулями, тем более что на практике соблюдение этого условия крайне неудобно. Приемник попросту выполняет CRC-деление полученной исходной строки (дополненной в конце
исходным значением CRC) на полином и анализирует остаток. Если остаток от этого деления нулевой, то исходная последовательность не была нарушена во время передачи. В обратном случае существует очень большая вероятность нарушения целостности исходной последовательности, и нужно принимать дополнительные меры по выяснению и исправлению ситуации. Одной из таких мер может быть попытка восстановления нужного значения CRC.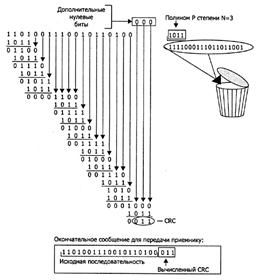

Рис. 9.5. Схема формирования выходного сообщения из исходного с использованием CRC-алгоритма

Описанный выше алгоритм вычисления значения CRC называется прямым и чаще всего реализуется аппаратно. Но, тем не менее, для совершенствования навыков программирования на ассемблере составим реализующий его пример программы. Хотя эффективность этой программы не слишком высока, у нее есть две учебные цели:

• показать в виде программной реализации суть алгоритма вычисления CRC и самого CRC-деления;
• подготовить себя к пониманию более совершенных алгоритмов расчета CRC, к которым относится, в частности, рассматриваемый ниже табличный алгоритм.

Для компьютерной реализации алгоритмов вычисления CRC удобно выбирать полиномы со степенями, кратными 8 (то есть размерности регистров) — 8, j5, 24, 32 или даже 64. В этом случае можно подобрать команды из системы команд микропроцессора, наиболее оптимально реализующие алгоритмы вычисления CRC. В качестве полинома выберем один из рекомендуемых полиномов (см. ниже) — 4003. И еще одно важное замечание — степень полинома определяет размерность регистра, используемого в алгоритме, при этом считается, что старший (всегда единичный) бит полинома находится сразу за левой границей регистра. В этих условиях программа реализации прямого алгоритма вычисления CRC функционирует следующим образом (для лучшего понимания в процессе разбора алгоритма см. рис. 9.6). В регистр побитно вдвигаются биты исходной строки. Это происходит до тех пор, пока при очередном сдвиге слева появится единичный бит. В этом случае все содержимое регистра подвергается операции XOR со значением полинома без старшего бита. Далее процесс сдвига и анализа выдвигаемого бита продолжается до тех пор, пока не будет выдвинут очередной единичный бит, в результате чего опять между регистром и полиномом выполняется операция XOR, и т. д. После того как последний бит вдвинут в регистр, в него вдвигается количество нулевых битов, равное степени полинома. Этим, как мы не раз уже отмечали, достигается участие всех бит исходной битовой строки в формировании значения CRC. В результате в регистре остается значение CRC, которое необходимо добавить к исходной строке и передать приемнику.

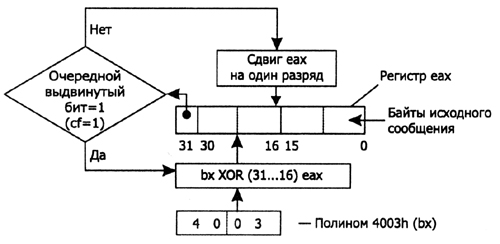
Рис. 9.6. Схема вычисления значения CRC прямым алгоритмом

Для того чтобы смоделировать действия стороны приемника, можно использовать ту же самую программу со слегка измененными исходными данными — к строке bitstring добавляем вычисленное значение CRC. После этого под отладчиком наблюдаем за процессом CRC-деления, причем контролируем остаток от деления. В определенный момент увидим, что он стал нулевым — это свидетельствует о том, что исходная последовательность не была изменена. Для эксперимента можно изменить значения одного или более битов исходной последовательности и посмотреть, что получится.

Недостатки алгоритма –

большое количество операций сдвига, операций XOR и операций условного перехода (так они выполняются для каждого бита сообщения).

13. Табличный алгоритм вычисления CRC.

Для того чтобы лучше понять суть табличного алгоритма вычисления CRC, обратимся опять к прямому методу, точнее к той схеме его вычисления (см. рис. 9.6), которая была реализована в приведенной выше программе.
Из этой схемы видно, что для текущего содержимого старшей половины регистра ЕАХ можно прогнозировать, как будет изменяться содержимое его битов по мере их сдвига. Для этого достаточно подвергнуть анализу его биты начиная с самого старшего. Допустим, что старшие 8 бит ЕАХ равны а7 а6 а5 а4 а3 а2 а, а,,. При следующем сдвиге (см. рис. 9.6) прямой алгоритм определяет, будет ли произведена операция XOR операнда с полиномом b7 b6 b5 b4 Ь3 b2 b, bо в ВХ (а7=1) или нет (а7=0). Если выдвинутый бит был равен 1, то прежнее содержимое старшей половины регистра ЕАХ будет подвергнуто операции XOR с соответствующими битами полинома. В обратном случае, если выдвинутый бит был равен 0, значения битов будут не изменены, а просто сдвинуты влево на одни разряд. В принципе, имея большое желание, можно рассчитать заранее, каким будет содержимое к-го бита в к-й итерации сдвига. К примеру, значение нового старшего бита, определяющего действия алгоритма в следующей итерации, можно рассчитать по содержимому двух старших битов старшего байта исходного операнда — а6 XOR а7 AND b7, где b7 — старший бит полинома (всегда равный единице).
Теперь остановимся для того, чтобы рассмотреть и обсудить очередную схему (рис. 9.7).

Рис. 9.7. Влияние на регистр ЕАХ серии операций XOR при вычислении CRC

Из рассуждений выше следует, что если взять для рассмотрения старший байт операнда, то по его содержимому можно однозначно предположить, сколько операций XOR и когда будет выполнено (см. рисунок). Обозначим старшую половину регистра ЕАХ как переменную А, а операнды со значениями полинома, объединяемые с А при единичном состоянии очередного выдвигаемого слева бита, обозначим соответственно как В, С, D (помним, что В = С = D). Тогда формирование результата Е можно представить формулой:

Е-((А [сдвиги| XOR В) [сдвигиj XOR С) |сдвиги| XOR D

Здесь | сдвиги | представляют собой значение от 0 до 7 и определяются теку щим содержимым старшего байта операнда (регистра ЕАХ). Благодаря ассоциативному свойству операции XOR тот же самый результат можно получить, если предварительно выполнить операцию XOR над полиномами В, С, D с соответствующими значениями сдвигов, а затем результат объединить по XOR с А:

F: = 1 сдвиги| XOR ( В |сдвиги| XOR С |сдвиги| XOR D) Е:= A XOR F

Из этих рассуждений следуют важные выводы:

• величина F является совершенно точно предсказуемой по содержимому старшего байта операнда;
• если величина F определяется содержимым старшего байта операнда и собственно значением полинома, то существует всего 256 возможных значений этой величины (по количеству значений, представимых беззнаковым байтом);
• исходя из первых двух положений величина F не зависит от значения операнда и может быть рассчитана заранее, при этом результаты ее расчетов можно свести в таблицу (!).

Вот мы и выяснили, на чем основано название табличного алгоритма расчета CRC. Теперь со знанием сути дела приведем его общее описание (рис. 9.8). В качестве основы для рассуждений по-прежнему используем программу прямого вычисления значения CRC и соответствующую схему (см. рис. 9.6).

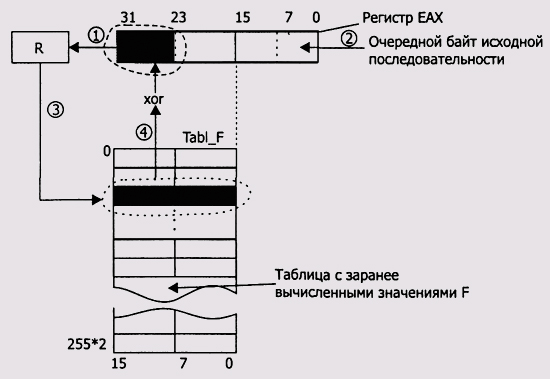
Рис. 9.8. Общая схема табличного алгоритма

На схеме, показанной на рисунке, цифрами обозначена последовательность шагов табличного алгоритма. Шаги 1 и 2 выполняются одновременно и означают, что старший байт из регистра ЕАХ выдвигается в переменную R, а младший байт этого регистра заполняется очередным байтом исходной последовательности. Значение переменной R используется на шаге 3 в качестве индекса в таблице TABL_F для извлечения 16-битного значения, которое на шаге 4 будет объединено
операцией XOR с содержимым старших 16 битов регистра ЕАХ. Таким образом, в отличие от прямого алгоритма процесс преобразования вырастает до уровня байтов и содержит три операции: сдвига, доступа к таблице для извлечения нужного значения и операции XOR извлеченного значения с содержимым старшей половины ЕАХ. По окончании процесса в старшей половине ЕАХ будет содержаться значение CRC. Сообщение по-прежнему должно быть выровненным, то есть дополненным количеством битов, равным степени полинома, или для данного случая — 16. Для практических приложений это крайне неудобно, и решение этой проблемы будет показано чуть ниже. Пока же разработаем программу вычисления содержимого таблицы на основе полинома 1021h степени 16.

:prg09_03.asm - программа вычисления содержимого таблицы :на основе полинома 1021п степени 16.
.data
tabl_16 dw 256 dup (0) :CRC-таблица
len_tabl_16=$-tabl_16
adr_tabl_16 dd tabl_16
polinom dw 1021h
.code
les di,adr_tabl_16
add di.len_tabl_16-2
std :идем назад по таблице
mov ex.255
mov bx.polinom
ml: xor ax.ax
mov ah.cl :индекс в таблице для вычисления CRC
push ex сложенные циклы
mov ex. 8
m2: shl ax.l
jnc m3 :старшие разряды не равны - выполняем сдвиг
: (частное нас не интересует) ;старшие разряды равны - выполняем XOR:
xor ax.bx :ax XOR polinom
m3: loop m2 _^
pop ex
stosw
loop ml

В результате работы этой программы область памяти tabl_16 будет инициализирована таблицей значений, которые могут быть использованы в схеме вычис-- ления значения CRC исходной последовательности (см. рис. 9.8).