КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Хеш-таблицы -10
1.Для хранения ключей, поступающих последовательно из массива Х, используется закрытое хеширование с функцией 
, задающей линейную последовательность проб. Определить правильный порядок хранения ключей в хеш-таблице H.
а)
| j | ||||||||||
|
б)
| j | ||||||||||
|
|
+в)
| j | ||||||||||
|
|
г)
| j | ||||||||||
|
|
д)Нет правильного варианта ответа.
2.Для хранения ключей, поступающих последовательно из массива Х, используется закрытое хеширование с функцией , задающей линейную последовательность проб. Определить правильный порядок хранения ключей в хеш-таблице H.
а)
| j | ||||||||||
|
|
б)
| j | ||||||||||
|
|
в)
| j | ||||||||||
|
| ||||||||||
+г)
| j | ||||||||||
|
|
д)Нет правильного варианта ответа.
3.Для хранения ключей, поступающих последовательно из массива Х, используется закрытое хеширование с функцией , задающей линейную последовательность проб. Определить правильный порядок хранения ключей в хеш-таблице H.
+а)
| j | ||||||||||
|
|
б)
| j | ||||||||||
|
|
в)
| j | ||||||||||
|
|
г)
| j | ||||||||||
|
|
д)Нет правильного варианта ответа.
4.Для хранения ключей, поступающих последовательно из массива Х, используется закрытое хеширование с функцией , задающей линейную последовательность проб. Определить правильный порядок хранения ключей в хеш-таблице H.
а)
| j | ||||||||||
|
|
+б)
| j | ||||||||||
|
|
в)
| j | ||||||||||
|
|
г)
| j | ||||||||||
|
|
д)Нет правильного варианта ответа.
5. Для хранения ключей, поступающих последовательно из массива Х, используется закрытое хеширование с функцией , задающей линейную последовательность проб. Определить правильный порядок хранения ключей в хеш-таблице H.
а)
| j | ||||||||||
|
|
б)
| j | ||||||||||
|
|
в)
| j | ||||||||||
|
|
+г)
| j | ||||||||||
|
|
д)Нет правильного варианта ответа.
6. Для хранения ключей, поступающих последовательно из массива Х, используется закрытое хеширование с функцией , задающей линейную последовательность проб. Определить правильный порядок хранения ключей в хеш-таблице H.
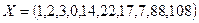
+а)
| j | ||||||||||
|
|
б)
| j | ||||||||||
|
|
в)
| j | ||||||||||
|
|
г)
| j | ||||||||||
|
|
д)Нет правильного варианта ответа.
Рекуррентное соотношение -15.
1.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для 
правильным ответом являются коэффициенты 6 и -4.
а)1
б)2
+в)-2
г)4
д)-10
+е)12
ж)-18
з) Нет нужного варианта ответа.
2.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
а)-5
+б)-10
в)17
г)20
+д)27
е)37
ж)-40
з) Нет нужного варианта ответа.
3.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
а)1
+б)-2
в)-3
г)-11
д)12
е)-13
+ж)20
з) Нет нужного варианта ответа.
4.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
а)-1
б)10
+в)-16
г)23
+д)29
е)-32
ж)44
з) Нет нужного варианта ответа.
5.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
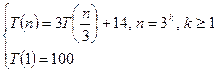
а)2
б)3
+в)-7
г)-20
д)102
+е)107
ж)-203
з) Нет нужного варианта ответа.
6.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
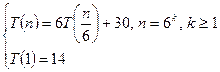
а)-3
+б)-6
в)9
г)10
+д)20
е)-30
ж)-40
з) Нет нужного варианта ответа.
7.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
а)2
+б)-4
в)6
г)-8
д)15
е)17
+ж)19
з) Нет нужного варианта ответа.
8.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
+а)-2
б)6
в)-8
+г)18
д)-32
е)64
ж)-100
з) Нет нужного варианта ответа.
9.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
+а)-1
б)3
в)-5
г)10
д)-52
е)101
+ж)201
з) Нет нужного варианта ответа.
10.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
+а)-1
б)-2
в)3
г)12
+д)18
е)21
ж)-36
з) Нет нужного варианта ответа.
11.Решить рекуррентное соотношение и указать для полученного многочлена коэффициент при старшей степени (задающей порядок роста функции, являющейся решением рекуррентного соотношения) и свободный член. Например, для правильным ответом являются коэффициенты 6 и -4.
а)1
б)-3
в)-4
+г)-10
д)16
е)19
ж)210
+з) Нет нужного варианта ответа.
Дата добавления: 2015-04-11; просмотров: 27; Нарушение авторских прав
