
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Следовательно, в расчётах механики грунтов, с учетом отмеченных допущений, можно использовать теорию упругости.
2. Определение напряжений в массиве грунта от сосредоточенной силы. (задача Буссинеско 1885 г.)
               Р Р
 0 0
 R R
 r M r M
 М1
Z М1
Z
| Определить значения вертикальных напряжений  zи касательных напряжений; zи касательных напряжений;  ; ;  в точке М, расположенной на площадке параллельной плоскости ограничивающий массив. в точке М, расположенной на площадке параллельной плоскости ограничивающий массив.
|
Задачу решаем в 3 этапа:
1) Определяем  R – в радиальном направлении
R – в радиальном направлении  R (в т. М)
R (в т. М)
2) Определяем  – в радиальном направлении (приложенном к площадке, параллельной плоскости ограничивающей массив).
– в радиальном направлении (приложенном к площадке, параллельной плоскости ограничивающей массив).
3) Определяем  z ;
z ;  ;
; 
1 этап:
Пусть под действием силы Р точка М – переместилась в точку М1
S – перемещение т. М
Можно записать
S =A  ; S1=A ; S1=A 
|
  cos 0° = 1 Smax R= 0 cos 0° = 1 Smax R= 0
  cos 90° = 0 Smin R= cos 90° = 0 Smin R=  А – коэффициент пропорциональности
А – коэффициент пропорциональности
|
Относительное перемещение точки:



 еR =
еR = 
 =
= 
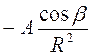
Согласно 1 постулата теории упругости между напряжениями и деформациями должна быть прямая зависимость, т.е.

 R = B еR =AB
R = B еR =AB  В – коэффициент пропорциональности
В – коэффициент пропорциональности
 АВ ?
АВ ?
 R – определяется как в сопромате («метод сечений» мысленно разрезают
R – определяется как в сопромате («метод сечений» мысленно разрезают
балку и оставшуюся часть уравновешивают).
Р
 зз зз
 R R 
|
Z
 Рассмотрим изменение
Рассмотрим изменение  в пределах
в пределах  Составим уравнение равновесия на ось Z:
Составим уравнение равновесия на ось Z:






 эп.
эп. 





 тогда
тогда 






















 Р
Y
Р
Y
 X
X 
 R
R
 М
М






 Z
Z




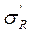 =
= 



 3 этап:
3 этап: ;
; 
 ;
; 

 ;
; 
 , подставим и получим
, подставим и получим ;
;  ;
;  ;
;  - опред. по таблице
- опред. по таблице  ;
; 
 в массиве грунта от действия нескольких сосредоточенных сил.
в массиве грунта от действия нескольких сосредоточенных сил.


 r3
r3


 K=f
K=f 
 при действии любой распределённой нагрузки (метод элементарного суммирования)
при действии любой распределённой нагрузки (метод элементарного суммирования)



















 Pi Pi=qifi
Z R
Pi Pi=qifi
Z R
 M r
элемент
M r
элемент
 М r
М r
 Pi – нагрузка на данный элемент
Pi – нагрузка на данный элемент
 szi =
szi = 

 Р
Р

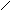
 Z M
Z M




 L
L – можно определить в интегральной форме
– можно определить в интегральной форме
 =
=  - при разворачивании этого интеграла получается очень громоздкая формула, поэтому её приводят к элементарному (простейшему) виду:
- при разворачивании этого интеграла получается очень громоздкая формула, поэтому её приводят к элементарному (простейшему) виду:

 ; где
; где  = f
= f 
 - в табл. СНиП, справочниках, учебниках.
- в табл. СНиП, справочниках, учебниках.







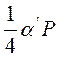 , но
, но  ,
а не 2Z, т.к. в1=2в
Разбив площадь подобным образом, можно записать
,
а не 2Z, т.к. в1=2в
Разбив площадь подобным образом, можно записать
 Р – интенсивность давления
Р – интенсивность давления


 Так мы сможем решить любую задачу по опред.
Так мы сможем решить любую задачу по опред. 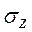 – на любом расстоянии и на любой глубине.
– на любом расстоянии и на любой глубине.












 Y
X Z
Y
X Z










 Р
Р


 в
в 












 изобары
изобары
 горизонтальные сечения, в результате можно найти такую систему точек, в которых
горизонтальные сечения, в результате можно найти такую систему точек, в которых  равны – соединив их – получим линии равных напряжений (изобары).
равны – соединив их – получим линии равных напряжений (изобары).


















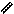






 в
в



 0,3 Р
0,3 Р 0,1 Р
0,1 Р Z
Z

 «Изохоры»
«Изохоры»













 Z
Z




















































 Влияние подстилающего слоя грунта
Еi – модуль деформации грунта
Влияние подстилающего слоя грунта
Еi – модуль деформации грунта


 Е2 Е1 = Е2
Е2 Е1 = Е2