
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тест 11. 1. Многоугольник называется правильным, если: 1) все его углы равны; 2) все его стороны равны; 3) в него можно вписать
| 1. | Многоугольник называется правильным, если: 1) все его углы равны; 2) все его стороны равны; 3) в него можно вписать окружность; 4) все углы и все стороны равны; 5) около него можно описать окружность. | 1) 1; 2) 2; 3) 3; 4) 4; 5) 5. |
| 2. | Выберите номер верного утверждения: Каждый последующий член возрастающей геометрической прогрессии, начиная со второго, может быть получен: 1) извлечением арифметического квадратного корня из предыдущего члена; 2) возведением предыдущего члена в квадрат; 3) в результате сложения предыдущего члена с одним и тем же числом; 4) возведение предыдущего члена в степень -1; 5) умножением предыдущего члена на одно и то же неравное нулю число. | 1) 1; 2) 2; 3) 3; 4) 4; 5) 5. |
| 3. | Определите, сколько простых чисел содержится в последовательности: 1; 2; 3; 15; 17; 23; 24; 46; 169; 289; 381 | 1) 3; 2) 4; 3) 5; 4) 6; 5) 7 |
| 4. | В четырёхугольник 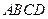 вписана окружность, вписана окружность,  . Длина стороны . Длина стороны  равна: равна:
| 1) 5; 2) 1; 3) 7; 4) 6; 5) 11. |
| 5. | Вычислите 
| 1) 22,5;
2) 150;
3) 45;
4) 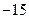 ;
5) 225 ;
5) 225
|
| 6. | Найдите количество целых решений неравенства  . .
| 1) 5; 2) 4; 3) 3; 4) 0; 5) 2. |
| 7. | Промежуток  является решением неравенства: является решением неравенства:
| 1)  ;
2) ;
2) 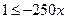 ;
3) ;
3)  ;
4) ;
4)  ;
5) ;
5) 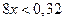 . .
|
| 8. | Сократите дробь:  . .
| 1)  ;
2) ;
2)  ;
3) ;
3)  ;
4) ;
4)  ;
5) ;
5)  . .
|
| 9. | При пересечении двух прямых образуются четыре угла, каждый из которых меньше развёрнутого. Найдите градусную меру меньшего угла, если один из образовавшихся углов составляет 60% суммы трёх остальных. | 1)  ;
2) ;
2)  ;
3) ;
3)  ;
4) ;
4)  ;
5) ;
5)  . .
|
| 10. | Укажите промежуток убывания функции 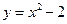 . .
| 1) 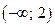 ;
2) ;
2) 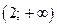 ;
3) ;
3) 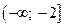 ;
4) ;
4)  5)
5)  . .
|
| 11. | Найдите отношение площади правильного треугольника, вписанного в окружность, к площади квадрата, описанного около этой окружности. | 1)  ;
2) ;
2)  ;
3) 3:16;
4) 1:2;
5) 3:4. ;
3) 3:16;
4) 1:2;
5) 3:4.
|
| 12. | Найдите значение 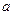 , если известно, что система , если известно, что система  имеет бесконечно много решений. имеет бесконечно много решений.
| 1) - 5; 2) 5; 3) 10; 4) - 10; 5) 0. |
| 13. | В параллелограмме 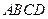 точка точка  середина стороны середина стороны  , ,  . Найдите длину диагонали . Найдите длину диагонали  , если отрезок , если отрезок 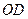 на 5 больше отрезка на 5 больше отрезка  . .
| |
| 14. | Найдите значение выражения 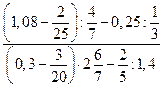
| |
| 15. | Основания трапеции равны 10 и 6. Найдите длину отрезка, соединяющего середины диагоналей трапеции. | |
| 16. | В двух школах поселка было 1500 учащихся. Через год число учащихся первой школы увеличилось на 10%, а второй на 20%, и в результате число учащихся школы стало 1720. Сколько учащихся было в первой школе первоначально? | |
| 17. | Найдите значение выражения  , где , где  - меньший, а - меньший, а  - больший корни уравнения - больший корни уравнения  . .
| |
| 18. | Точка О – середина боковой стороны  прямоугольного равнобедренного прямоугольного равнобедренного  , точка Р делит гипотенузу в отношении 1:3, считая от точки В. Найдите квадрат длины отрезка ОР, если , точка Р делит гипотенузу в отношении 1:3, считая от точки В. Найдите квадрат длины отрезка ОР, если 
| |
| 19. | Найдите меньший корень уравнения 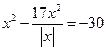
| |
| 20. | Найдите сумму чисел, обратных числам М и D, если  , ,  . .
|
Дата добавления: 2015-04-11; просмотров: 204; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Практическое занятие 2. Практическое занятие 1 |