
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
|
Движение по окружности с постоянной по модулю скоростью
| А 1
| Период обращения тела, движущегося равномерно по окружности, увеличился в 2 раза. Частота обращения
| | |
| 1) возросла в 2 раза
| 2) уменьшилась в 2 раза
| | |
| 3) возросла в 4 раза
| 4) уменьшилась в 4 раза
| | | А 2
| Материальная точка, двигаясь равномерно по окружности, за 3 с прошла четверть окружности. Определите частоту обращения точки
| |
| 1)  2) 2) 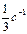
| 3) 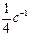 4) 4) 
| | А 3
| Когда период вращения Земли вокруг своей оси самый короткий?
| | |
| 1) летом
| 2) зимой
| | |
| 3) весной и осенью
| 4) всегда одинаковый
| | | А 4
| Период обращения Земли вокруг Солнца равен одному году, радиус орбиты Земли равен 150 млн. км. Скорость движения Земли по орбите равна примерно
| | |
| 1) 30 м/с
| 2) 30 км/с
| | |
| 3) 150 км/с
| 4) 1800 км/с
| | | А 5
| На кольцевой гонке два автомобиля движутся так, что все время радиус движения второго автомобиля в 2 раза больше первого, а периоды движения равны. Отношение скоростей  равно … равно …
| | |
| 1) 0,5
| 2) 2
| | |
| 3) 
| 4) 4
| | | | | | | |
| А 6
| По окружностям с радиусами R1 и R2 равномерно движутся две материальные точки со скоростями 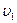 и и 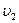 соответственно. Периоды их обращения одинаковы. Для данного случая справедливо равенство соответственно. Периоды их обращения одинаковы. Для данного случая справедливо равенство
| |
| 1)  2) 2) 
| 3)  4) 4) 
| | А 7
| Две материальные точки движутся по окружностям радиусами  и и  с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
| |
| 1)  2) 2)  3) 3)  4) 4) 
| | А 8
| По окружностям с радиусами R1 и R2 равномерно движутся две материальные точки со скоростями 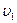 и и 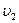 соответственно. Частоты их обращения одинаковы. Для данного случая справедливо равенство соответственно. Частоты их обращения одинаковы. Для данного случая справедливо равенство
| |
| 1)  2) 2) 
| 3)  4) 4) 
| | А 9
| По окружностям одинакового радиуса равномерно движутся две материальные точки со скоростями 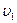 и и 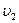 соответственно. Частота обращения первой точки в 2 раза меньше частоты обращения второй. Для данного случая справедливо равенство: соответственно. Частота обращения первой точки в 2 раза меньше частоты обращения второй. Для данного случая справедливо равенство:
| |
| 1)  2) 2) 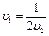
| 3)  4) 4) 
| | А 10
| По окружностям одинакового радиуса равномерно движутся две материальные точки со скоростями 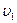 и и 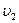 соответственно. Частота обращения первой точки в 2 раза больше частоты обращения второй. Для данного случая справедливо равенство: соответственно. Частота обращения первой точки в 2 раза больше частоты обращения второй. Для данного случая справедливо равенство:
| |
| 1) 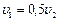 2) 2) 
| 3)  4) 4) 
| | А 11
| Две материальные точки равномерно движутся по окружностям одинакового радиуса, при этом линейная скорость первой точки в 2 раза меньше линейной скорости второй точки. Частоты обращения точек по окружностям связаны соотношением:
| |
| 1)  2) 2) 
| 3)  4) 4) 
| | А 12
| К боковой поверхности цилиндра, вращающегося вокруг своей оси, прижимают второй цилиндр с осью, параллельной оси первого, и радиусом, вдвое превосходящим радиус первого. При совместном вращении двух цилиндров без проскальзывания у них совпадают
| | |
| 1) периоды вращения
2) частоты вращения
3) линейные скорости точек на поверхности
4) центростремительные ускорения точек на поверхности
| | | | | | |
| В 1
| Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 20 см делает 20 оборотов за 10 с. Сколько оборотов в секунду делает шестерня радиусом 10 см?
| | В 2
| Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Большая шестерня радиусом 10 см делает 20 оборотов за 10 с, а частота обращения меньшей шестерни равна 5 Гц. Каков радиус меньшей шестерни? Ответ укажите в сантиметрах.
| | В 3
| Две шестерни, сцепленные друг с другом, вращаются вокруг неподвижных осей. Отношение периодов вращения шестерен равно 3. Радиус меньшей шестерни равен 6 см. Каков радиус большей шестерни? Ответ укажите в сантиметрах.
| | А 13
| Диск радиусом 20 см равномерно вращается вокруг своей оси. Скорость точки, находящейся на расстоянии 15 см от центра диска, равна 1,5 м/с. Скорость крайних точек диска равна
| |
| 1) 4 м/с
| 2) 0,2 м/с
| |
| 3) 2 м/с
| 4) 1,5 м/с
| | А 14
| При равномерном движении по окружности модуль вектора изменения скорости при перемещении из точки А в точку В (см. рис.) равен
| 
| |
| 1) 0
| 2) 
| |
| 3) 
| 4) 
| | А 15
| Вектор ускорения при равномерном движении точки по окружности
| |
| 1) постоянен по модулю и по направлению
2) равен нулю
3) постоянен по модулю, но непрерывно изменяется по направлению
4) постоянен по направлению, но непрерывно изменяется по модулю
| |
| | А 16
| Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение максимально?
| 
| |
| 1) 1
| |
| 2) 2
| |
| 3) 3
| |
| 4) Во всех точках одинаково
| | А 17
| Автомобиль движется по закруглению дороги радиусом 20 м с центростремительным ускорением 5 м/с2. Скорость автомобиля равна
| | |
| 1) 12,5 м/с 2) 10 м/с
| 3) 5 м/с 4) 4 м/с
| | | А 18
| Две материальные точки движутся по окружностям радиусами  и и 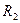 , причём , причём  . При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением . При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
| |
| 1) 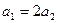 2) 2) 
| 3)  4) 4) 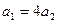
| | А 19
| Два спутника движутся по разным круговым орбитам вокруг Земли. Скорость первого из них в 2 раза больше, а радиус орбиты в 4 раза меньше, чем у второго. Центростремительное ускорение первого спутника  , а второго - , а второго -  . Чему равно отношение . Чему равно отношение  ? ?
| | |
| 1) 1
| 2) 2
| | |
| 3) 4
| 4) 16
| | | В 4
| Рассчитайте центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси координат которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли. Ответ округлите до двух значащих цифр. Радиус Земли 6400 км, а период вращения вокруг оси равен 1 суткам .
| | | В 5
| Материальная точка движется с постоянной скоростью по окружности радиусом  . Как изменятся перечисленные в первом столбце физические величины, если скорость точки увеличится? . Как изменятся перечисленные в первом столбце физические величины, если скорость точки увеличится?
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
| ИХ ИЗМЕНЕНИЕ
| | А) Угловая скорость
| 1) увеличится
| | Б) Центростремительное ускорение
| 2) уменьшится
| | В) Период обращения по окружности
| 3) не изменится
|
| |
|

 2)
2) 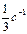
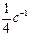 4)
4) 
 равно …
равно …

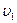 и
и 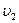 соответственно. Периоды их обращения одинаковы. Для данного случая справедливо равенство
соответственно. Периоды их обращения одинаковы. Для данного случая справедливо равенство
 2)
2) 
 4)
4) 
 и
и  с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
с одинаковыми по модулю скоростями. Их периоды обращения по окружностям связаны соотношением
 2)
2)  3)
3)  4)
4) 
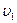 и
и 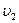 соответственно. Частоты их обращения одинаковы. Для данного случая справедливо равенство
соответственно. Частоты их обращения одинаковы. Для данного случая справедливо равенство
 2)
2) 
 4)
4) 
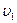 и
и 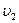 соответственно. Частота обращения первой точки в 2 раза меньше частоты обращения второй. Для данного случая справедливо равенство:
соответственно. Частота обращения первой точки в 2 раза меньше частоты обращения второй. Для данного случая справедливо равенство:
 2)
2) 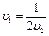
 4)
4) 
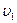 и
и 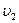 соответственно. Частота обращения первой точки в 2 раза больше частоты обращения второй. Для данного случая справедливо равенство:
соответственно. Частота обращения первой точки в 2 раза больше частоты обращения второй. Для данного случая справедливо равенство:
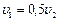 2)
2) 
 4)
4) 
 2)
2) 
 4)
4) 





 и
и 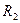 , причём
, причём  . При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
. При условии равенства линейных скоростей точек их центростремительные ускорения связаны соотношением
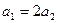 2)
2) 
 4)
4) 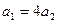
 , а второго -
, а второго -  . Чему равно отношение
. Чему равно отношение  ?
?
 . Как изменятся перечисленные в первом столбце физические величины, если скорость точки увеличится?
. Как изменятся перечисленные в первом столбце физические величины, если скорость точки увеличится?
