Операции с векторными величинами (справочный материал).

Вектор – направленный отрезок. Векторные величины имеют числовое значение (модуль), на­правление, точку приложения.

Проекция вектора а на ось Ох – длина отрезка, соединяющего проекцию начала вектора на ось Ох с проекцией конца вектора на ту же ось. Она равна произведению модуля этого вектора на косинус уг­ла между направлением оси и вектора: .

Проекция вектора может быть положительной, отрицательной и равной нулю:

- если угол между направлением вектора и осью острый, то cos α > 0 => a_х > 0 (рис. а);

- если угол между направлением вектора и осью тупой, cos α < 0 => a_х< 0 (рис. б);

- если угол между направлением вектора и осью прямой (α = 90°), то cos 90° = 0 => a_х =0 (рис. в).

Модуль векторной величины можно определить через проекции вектора на оси Ох и Оу (рис. г):

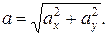
При умножении векторной величины на скаляр получим вектор, коллинеарный данному: .

Сложение векторов по правилу треугольника: параллельным переносом совмещается начало второго вектора с концом первого, начало третье­го – с концом второго и т.д.; тогда сумма векто­ров – это вектор, соединяющий начало первого вектора с концом последнего.

Сложение двух векторов по правилу треугольника: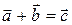

Сложение трех векторов по правилу треугольника: .

Сложение векторов по правилу параллелограм­ма: параллельным переносом совмещаются начала двух векторов; тогда сумма векторов – диагональ построенная на этих векторах, как на сторонах па­раллелограмма.

Сложение двух векторов по правилу па­раллелограмма:

Сложение трех векторов по правилу па­раллелограмма:.

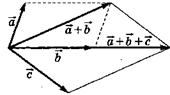
Вычитание векторов по правилу треугольника: совмещаются начала двух векторов; тогда раз­ность векторов – это вектор, соединяющий их концы. Он направлен в сторону уменьшаемого вектора: .

Проекция суммы векторов на координатную ось равна сумме проекций слагаемых векторов на ту же ось: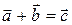

Ох

Оy

Относительность механического движения со­стоит в том, что вид траектории, путь и перемеще­ние зависят от выбора системы отсчета.

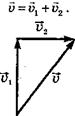
Классический закон сложения скоростей: скорость тела относительно системы, принятой за неподвижную, равна геометрической сумме скорости тела в подвижной системе отсчета и ско­рости самой подвижной системы отсчета относительно неподвижной:

Неравномерное движение. Средняя и мгновенная скорости. Равномерное и равноускоренное движения. Ускорение. Графики зависимости кинематических величин от времени при равномерном и равноускоренном движениях.

2.1. Равномерное движение.

Прямолинейным равномерным движением на­зывают движение, при котором тело (материаль­ная точка) за любые равные промежутки времени совершает одинаковое перемещение, или движе­ние с постоянной скоростью вдоль прямой.

Скорость – векторная физическая величина, характеризующая перемещение тела в единицу времени.

В SI единица скорости: (метр в секунду: 1 м/с)

Метр в секунду равен скорости прямолинейного равномерного движения точки, при котором тючка перемещается за единицу времени (1 с) на единицу длины (1 м).

Скорость равномерного прямолинейного движения численно равна отношению достаточно малого перемещения тела ко времени движения:

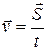
Уравнение равномерного прямолинейного дви­жения тела х = x(t).

Проекция перемещения на координатную ось равна изменению координаты (разности конечной и начальной координат): .

Решение основной задачи механики для равномерного прямолинейного движения: .

Уравнение движения в скалярном виде: .

Если тело движется вдоль оси Ох, то 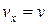, ес­ли против, то .

График проекции перемещения при равно­мерном прямолинейном движении:

График проекции скорости равномерного пря­молинейного движения ( ):

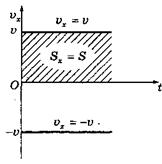
Геометрический смысл перемещения: По графику скорости можно определить проекцию перемещения как площадь фигуры, ограниченной графиком скорости, осью времени и двумя ордината­ми, соответствующими начальному и конечному мо­ментам времени. Это утверждение справедливо также и для равноускоренного прямолинейного движения.

График равномерного прямолинейного движе­ния ( ):

2.2. Неравномерное движение.

Мгновенная скорость тела – скорость тела в дан­ный момент времени в данной точке траектории: .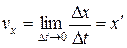

Средняя скорость – это величина, равная от­ношению перемещения ко времени, в течение ко­торого оно произошло: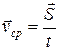

Средняя путевая скорость – величина, равная отношению пути ко времени, за которое он пройден: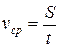

При прямолинейном однонаправленном дви­жении средняя путевая скорость равна модулю средней скорости: .

 

2.3. Равноускоренное движение.

Равноускоренным прямолинейным движением тела называют такое движение, при котором его скорость за любые равные промежутки времени изменяется на одинаковые величины, или движе­ние с постоянным ускорением вдоль прямой: а = const.

Ускорение тела при равноускоренном движе­нии – векторная физическая величина, характеризующая быстроту изменения величины скорости.

Ускорение равноускоренного прямолинейно­го движения численно равно отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло: .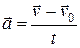

В случае ускоренного движения мгновенное ускорение равно:

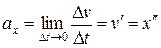
В SI единица ускорения: 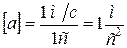(метр в секунду за секунду).

 

1 м/с² равен ускорению такого равноускорен­ного движения тела, при котором за единицу времени (1с) скорость тела изменяется на единицу скорости (1 м/с).

Проекция конечной мгновенной скорости на ось Ох при равноускоренном прямолинейном движении: .

Уравнение мгновенной скорости в скалярном виде: .

В уравнении 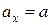, если тело ускоря­ется; 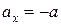, если тело замедляется.

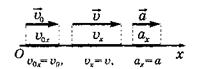
Уравнения равноускоренного прямолинейного движения в векторной форме:

;

.

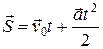Уравнения равноускоренного прямолинейного движения в проекции на ось Ох:

;

 

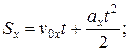
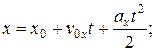
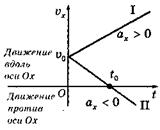
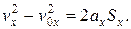
График скорости равноускоренного прямоли­нейного движения: тело I ускоряет свое движение вдоль оси Ох, тело II — замедляет; в момент времени t₀ оно останавливается и движется ускоренно в направлении, противоположном оси Ох.

График движения при равноускоренном прямо­линейном движении – парабола. Графики движения соответствуют графикам скорости. Здесь t₀ – момент времени, соответствующий остановке тела, является вершиной параболы II.

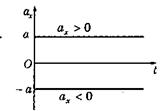
График ускорения равноускоренного прямоли­нейного движения.