
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: Кинематика поступательного и вращательного движения. 1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем
1. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем, как показано на графике.
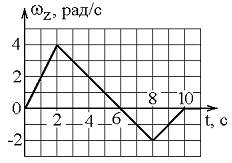
Угловое перемещение (в радианах) в промежутке времени от 4 с до 8 с равно …

| |||
Решение:
По определению 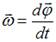 . Отсюда
. Отсюда 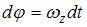 и
и 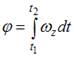 (индекс z у
(индекс z у  не пишем. Считаем, что
не пишем. Считаем, что  может быть положительным и отрицательным). Используя геометрический смысл интеграла, искомый угол можно найти как площадь двух треугольников. Площадь первого (от 4 с до 6 с)- поворот на угол
может быть положительным и отрицательным). Используя геометрический смысл интеграла, искомый угол можно найти как площадь двух треугольников. Площадь первого (от 4 с до 6 с)- поворот на угол 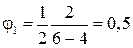 рад, площадь второго (от 6 с до 8 с)- поворот на угол
рад, площадь второго (от 6 с до 8 с)- поворот на угол  рад ( в обратном направлении). Следовательно, с 4 по 8 с тело повернется на угол
рад ( в обратном направлении). Следовательно, с 4 по 8 с тело повернется на угол  рад.
рад.
2. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется со временем, как показано на графике:
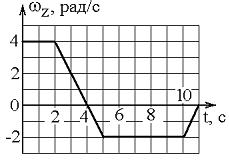
Через 11 с тело окажется повернутым относительно начального положения на угол ___ 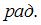

| |||
Решение:
По определению 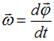 . Отсюда
. Отсюда 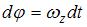 и
и  .(индекс z у
.(индекс z у  не пишем. Считаем, что
не пишем. Считаем, что  может быть положительным и отрицательным). Используя геометрический смысл интеграла, искомый угол можно найти как площадь трапеции. Через 4 с после начала вращения тело повернется на угол
может быть положительным и отрицательным). Используя геометрический смысл интеграла, искомый угол можно найти как площадь трапеции. Через 4 с после начала вращения тело повернется на угол 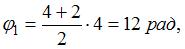 еще через 7 с – на угол
еще через 7 с – на угол 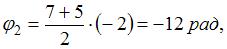 но в обратном направлении. Следовательно, через 11 с тело повернется на угол
но в обратном направлении. Следовательно, через 11 с тело повернется на угол 
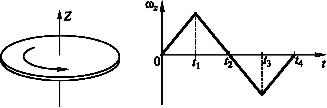
3. Диск вращается вокруг своей оси, изменяя проекцию угловой скорости  так, как показано на рисунке. Вектор угловой скорости
так, как показано на рисунке. Вектор угловой скорости 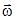 и вектор углового ускорения
и вектор углового ускорения  направлены в одну сторону в интервалы времени …
направлены в одну сторону в интервалы времени …

| от 0 до 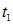 и от и от 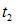 до до 
| ||
от 0 до 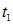 и от и от 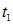 до до 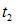
| |||
от 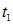 до до 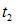 и от и от 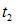 до до 
| |||
от 0 до 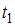 и от и от 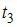 до до 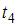
|
Решение:
По определению угловое ускорение тела 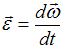 , где
, где  – его угловая скорость. При вращении вокруг неподвижной оси векторы
– его угловая скорость. При вращении вокруг неподвижной оси векторы  и
и  коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора
коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора  связано с направлением вращения тела правилом правого винта. В интервале времени от 0 до
связано с направлением вращения тела правилом правого винта. В интервале времени от 0 до 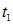 вектор угловой скорости направлен вдоль оси OZ и, поскольку скорость увеличивается ( растет модуль проекции), вектор углового ускорения направлен так же. В интервале времени от
вектор угловой скорости направлен вдоль оси OZ и, поскольку скорость увеличивается ( растет модуль проекции), вектор углового ускорения направлен так же. В интервале времени от  до
до 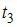 вектор угловой скорости направлен против оси OZ, но скорость при этом также увеличивается ( растет модуль проекции), следовательно, вектор углового ускорения сонаправлен с вектором угловой скорости.
вектор угловой скорости направлен против оси OZ, но скорость при этом также увеличивается ( растет модуль проекции), следовательно, вектор углового ускорения сонаправлен с вектором угловой скорости.
4. Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.
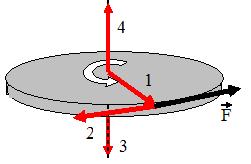
При этом правильно изображает направление углового ускорения диска вектор …

| |||
Решение:
По определению угловое ускорение тела 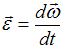 , где
, где  – его угловая скорость. При вращении вокруг неподвижной оси векторы
– его угловая скорость. При вращении вокруг неподвижной оси векторы  и
и  коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора
коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора  связано с направлением вращения тела правилом правого винта. В данном случае вектор
связано с направлением вращения тела правилом правого винта. В данном случае вектор  ориентирован в направлении 4, и, так как после приложения силы движение становится ускоренным, вектор
ориентирован в направлении 4, и, так как после приложения силы движение становится ускоренным, вектор  ориентирован в направлении 4.
ориентирован в направлении 4.
5. Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.
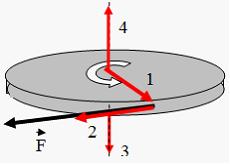
До остановки диска правильно изображает направление угловой скорости вектор …

| |||
Решение:
Направление вектора угловой скорости  связано с направлением вращения тела правилом правого винта. В данном случае вектор
связано с направлением вращения тела правилом правого винта. В данном случае вектор  ориентирован в направлении 4. После приложения силы движение становится замедленным.
ориентирован в направлении 4. После приложения силы движение становится замедленным.
6. Частица из состояния покоя начала двигаться по дуге окружности радиуса 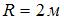 с угловой скоростью, модуль которой изменяется с течением времени по закону
с угловой скоростью, модуль которой изменяется с течением времени по закону  . Отношение нормального ускорения к тангенциальному через 2 секунды равно …
. Отношение нормального ускорения к тангенциальному через 2 секунды равно …

| |||
Решение:
Нормальное ускорение частицы равно 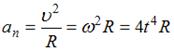 , где R – радиус кривизны траектории. Тангенциальное ускорение определяется выражением
, где R – радиус кривизны траектории. Тангенциальное ускорение определяется выражением 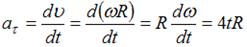 . Следовательно, отношение нормального ускорения к тангенциальному через 2 с равно
. Следовательно, отношение нормального ускорения к тангенциальному через 2 с равно  .
.
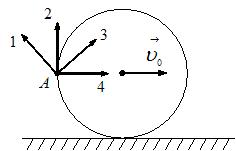
7. Диск катится равномерно по горизонтальной поверхности со скоростью 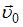 без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …
без проскальзывания. Вектор скорости точки А, лежащей на ободе диска, ориентирован в направлении …

| |||
Решение:
Качение однородного кругового цилиндра (диска) по плоскости является плоским движением. Плоское движение можно представить как совокупность двух движений: поступательного, происходящего со скоростью 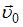 центра масс, и вращательного вокруг оси, проходящей через этот центр. Тогда
центра масс, и вращательного вокруг оси, проходящей через этот центр. Тогда  . Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что
. Поскольку диск катится без проскальзывания, скорость точки диска, соприкасающейся с поверхностью, равна нулю. Отсюда следует, что 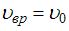 (Нарисовать вектор
(Нарисовать вектор  вр в точке касания плоскости). Вектор
вр в точке касания плоскости). Вектор 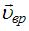 направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 2). Тогда вектор скорости
направлен по касательной к окружности в рассматриваемой точке (для точки А – в направлении 2). Тогда вектор скорости 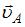 точки А ориентирован в направлении 3.
точки А ориентирован в направлении 3.
8. Твердое тело вращается вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси, изменяется со временем в соответствии с графиком, представленным на рисунке.
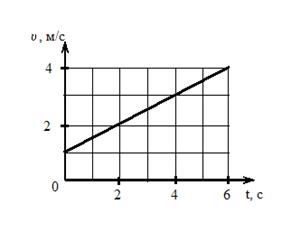
Угловое ускорение тела (в единицах СИ) равно …

| |||
| 0,5 | |||
| 0,05 | |||
Решение:
По определению угловое ускорение тела, вращающегося вокруг неподвижной оси, 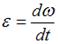 (неверно, правильно
(неверно, правильно 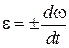 ), где
), где 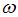 – угловая скорость тела. Связь между модулями угловой скорости вращения тела и линейной скоростью точки, отстоящей от оси вращения на расстояние R, имеет вид
– угловая скорость тела. Связь между модулями угловой скорости вращения тела и линейной скоростью точки, отстоящей от оси вращения на расстояние R, имеет вид  . Отсюда
. Отсюда 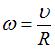 , причем R = 10 см = 0,1 м. Из представленного графика начальная скорость
, причем R = 10 см = 0,1 м. Из представленного графика начальная скорость 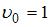 м/с, ускорение
м/с, ускорение  Итак, зависимость скорости точки от времени в единицах СИ задается уравнением
Итак, зависимость скорости точки от времени в единицах СИ задается уравнением 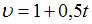 , а зависимость угловой скорости вращения тела – уравнением
, а зависимость угловой скорости вращения тела – уравнением  . ( Т.к.
. ( Т.к. 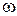 возрастает со временем, то
возрастает со временем, то  и) Тогда
и) Тогда 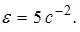
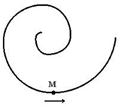
9. Точка М движется по спирали с равномерно убывающей скоростью в направлении, указанном стрелкой. При этом величина полного ускорения точки …

| уменьшается | ||
| увеличивается | |||
| не изменяется | |||
| равна нулю |
Решение:
Величина полного ускорения определяется соотношением  , где
, где  и
и 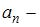 (проекция) тангенциальное и нормальное ускорения соответственно, причем
(проекция) тангенциальное и нормальное ускорения соответственно, причем  ,
,  , где R – радиус кривизны траектории. Так как по условию скорость убывает равномерно (т.е. линейно со временем ), величина тангенциального ускорения остается постоянной. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка ( а скорость уменьшается по условию задачи). Таким образом, полное ускорение точки уменьшается.
, где R – радиус кривизны траектории. Так как по условию скорость убывает равномерно (т.е. линейно со временем ), величина тангенциального ускорения остается постоянной. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка ( а скорость уменьшается по условию задачи). Таким образом, полное ускорение точки уменьшается.
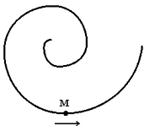
10. Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения …
| уменьшается | ||
| увеличивается | ||
| не изменяется |
Решение:
Величина полного ускорения определяется соотношением  , где
, где  и
и 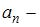 (проекция) тангенциальное и нормальное ускорения соответственно, причем
(проекция) тангенциальное и нормальное ускорения соответственно, причем  ,
,  , где R – радиус кривизны траектории. Так как по условию скорость постоянна, то величина тангенциального ускорения равна нулю. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка.
, где R – радиус кривизны траектории. Так как по условию скорость постоянна, то величина тангенциального ускорения равна нулю. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка.
11. Тело движется с постоянной по величине скоростью по траектории, изображенной на рисунке:

Для величин полного ускорения а тела в точках А и В справедливо соотношение …

| 
| ||
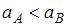
| |||
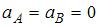
| |||
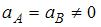
|
Решение:
Величина полного ускорения определяется соотношением  , где
, где  и
и 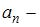 (проекция) тангенциальное и нормальное ускорения соответственно, причем
(проекция) тангенциальное и нормальное ускорения соответственно, причем  ,
,  , где R – радиус кривизны траектории. Так как по условию скорость по величине постоянна, то тангенциальное ускорение всюду равно нулю. В то же время величина нормального ускорения в точке А больше, чем в точке В, поскольку радиус кривизны траектории в точке А меньше, чем в точке В, что видно из рисунка. Таким образом, величина полного ускорения в точке А больше, чем в точке В.
, где R – радиус кривизны траектории. Так как по условию скорость по величине постоянна, то тангенциальное ускорение всюду равно нулю. В то же время величина нормального ускорения в точке А больше, чем в точке В, поскольку радиус кривизны траектории в точке А меньше, чем в точке В, что видно из рисунка. Таким образом, величина полного ускорения в точке А больше, чем в точке В.
12.Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.

Нормальное ускорение  на участке А-В-С …
на участке А-В-С …
| уменьшается | ||
| увеличивается | ||
| не изменяется |
Решение :
Величина полного ускорения определяется соотношением  , где
, где  и
и 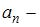 (проекция) тангенциальное и нормальное ускорения соответственно, причем
(проекция) тангенциальное и нормальное ускорения соответственно, причем  ,
,  , где R – радиус кривизны траектории. Полное ускорение равно g Следовательно,
, где R – радиус кривизны траектории. Полное ускорение равно g Следовательно,  .Т.к. в верхней точке траектории
.Т.к. в верхней точке траектории  , то, очевидно, что
, то, очевидно, что  на указанном участке увеличивается ( сделать рисунок).
на указанном участке увеличивается ( сделать рисунок).
13. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.

Модуль полного ускорения камня …
во всех точках одинаков
максимален в точках А и Е
максимален в точках В и D
максимален в точке С
Решение:
Величина полного ускорения равна g (Определяется силой, действующей на тело после начала броска). Следовательно, модуль полного ускорения камня во всех точках одинаков
Дата добавления: 2015-04-15; просмотров: 1849; Мы поможем в написании вашей работы!; Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Тема: Кинематика поступательного и вращательного движения | | | Виды договоров при оформлении отношений со спортсменами. |