Выполнение задания

Аналитическое описание

Экспериментальных зависимостей

Компьютерный подбор оптимального уравнения регрессии.

Анализируемый процесс может быть описан в математической форме, при этом используемые эмпирические формулы могут иметь различный вид. Поэтому выбор оптимального уравнения диктуется только одним соображением – данные теоретического расчёта (т.е. полученные из уравнения) должны в наибольшей степени совпадать с фактическими результатами.

Рассмотрим на конкретном примере возможность решения подобной задачи с использованием приложения Excel.

Обсуждается следующая задача:

Проведено N=6 опытов по изучению некоторой зависимости y=f(x) . В каждом варианте опыты повторялись n раз, при этом число параллельных измерений для каждого конкретного варианта опыта могло заметно различаться (от 3 дублей до 5). Полученные экспериментальные данные представить в табличной форме.

Надлежит выполнить следующие процедуры:

1. Провести первичную статистическую обработку экспериментальных данных с выявлением грубых промахов, определением среднеквадратичного отклонения и вычислением доверительного интервала для уровня значимости a=0,05.

2. Построить график рассматриваемой зависимости и подобрать для неё эмпирическую формулу.

3. Дать статистическую оценку подобранному уравнению.

Приступим к решению данного примера. Удобнеё всего придерживаться привычного алгоритма, т.е. будем указывать пошаговую последовательность наших манипуляций при работе с компьютером.

Выполнение задания

1. Сначала запускаем Excel и открываем рабочий лист, в котором мы и будем формировать наш документ.

2. Пользуясь исходными данными, указанными в методическом указании заполняем таблицу, т.е. указываем номера опытов, значения аргумента хивсе значения функции ув параллельных опытах (Рис.1).

Рис.1 Номера опытов, значения аргумента хизначения функции у

3. Далее добавим к нашей таблице ещё три столбца, в которые будут введены среднее арифметическоеx, среднеквадратичное отклонение S_n и доверительный интервал Dх для каждого опыта, т.е. итоговые расчеты для каждой строки. Начинаем вычисление. Для этого нужно воспользоваться Мастером функций. Перед запуском Мастера нужно выделить ту ячейку, в которую будет помещён искомый результат. Например, для определения среднего арифметического значения данных первой строки активизируем верхнюю ячейку предпоследней колонки. Затем запустим Мастер функций (кнопкой f_x. или же в строке меню используем команды Вставка/Функция).

Действия Мастера функций:

· в появившемся диалоговом окне следует выбрать нужную функцию из списка (все функции разбиты на категории). Для этого в левой части панели (там перечислены категории) выберем требуемую под названием Статистические, затем в правой части, где указаны функции, активизируем собственно нужную функцию Срзнач и далеё нажмём на кнопку ОК (Рис.2);

Рис.2 СРЗНАЧ

· выделим теперь все ячейки первой строки, относящиеся к параметру y, т.е. это те ячейки, где расположены дубли первого опыта. После чего – кнопка ОК. Если теперь взглянуть на содержимое ячейки среднего арифметического, то там и будет указан полученный результат (Рис.3).

Рис.3 Аргументы функции

4. Далеё полагалось бы подобную процедуру проделать для всей матрицы (таблицы). Делаем следующеё. Выделим ячейку, где содержится среднее арифметическое, и протянем Маркер заполнения(маленький квадратик в правом нижнем углу) вдоль всей предпоследней колонки вниз. Что получим? Во всех соответствующих ячейках будут содержаться готовые расчётные данные среднего значения!

Подобные манипуляции проделываем и для следующей колонки – среднеквадратичного (стандартного) отклонения. Сделаем только одно пояснение. При работе с Мастером функций нужно будет активизировать функцию Стандотклон.

Если окажется, что число знаков после запятой велико, то разрядность можно отрегулировать, активизировав соответствующую ячейку с данным числом, а затем в инструментальной строке использовать команду «Уменьшить разряд».

5. Для расчёта доверительного интервала используем те же опции посредством Мастера функций. Нужно выделить функцию Доверит, а затем в появившемся окне Аргументы функции заполнить запрашиваемые строки. Для уровня значимости α укажем 0,05; затем введем значение уже рассчитанного стандартного отклонения S_n и число дублей n =4.

Теперь пришел черёд проверить имеющиеся экспериментальные данные на наличие грубого промаха. Так, шестой серии настораживает результат 5-го измерения. Проверку надлежит провести по методу максимального относительного отклонения. Допустим, выполненные расчёты показали, что с вероятностью 95% этот результат следует признать грубым промахом (он не соответствует данной числовой совокупности). По этой причине его надлежит исключить из дальнейшего рассмотрения (т.е. в окончательном варианте число дублей первого опыта составит n=4) (Рис.4).

Казалось бы, в очередной раз придется заняться расчётом среднего и стандартного отклонения (в данном случае для первой строки). Однако поступим следующим образом. Выделим ту ячейку, в которой содержится выскакивающий результат, и нажмём клавишу Delete. Ячейка станет свободной, но при этом автоматически поменяются значения Срзначи Стандотклон.

Рис.4 Аргументы функции

6. В результате получаем полную таблицу (Рис.5).

Рис.5 Итоговый результат

7. Наконец, приступим к самому интересному этапу нашего задания – строим в графической форме анализируемую зависимость. В этом случае нам будет помогать Мастер диаграмм. Он запускается либо нажатием клавиши на стандартной панели инструментов, либо через команды Вставка/Диаграмма в строке меню.

8. Запустим Мастер диаграмм и выполним рекомендации первого шага – выберем тип диаграммы. В появившемся окне, в левой его части, высветим тип диаграммы – График. Здесь же, нажав кнопку «Просмотр результата», можно будет посмотреть, как станут выглядеть наши данные на диаграмме выбранного типа.

9. Нажмём на клавишу «Далее» и перейдём, следовательно, ко второму шагу. В окне будет активизирована вкладка «Диапазон данных». Теперь в кнопке Ряды в следует указать, что наши данные представлены в Столбцах. Отметим, что на оси ординат будут указаны заданные численные значения аргумента, а вот на оси абсцисс пока содержатся некие нейтральные показатели типа 1, 2, 3 и проч.

10. В пределах окна второго шага высветим вкладку «Ряд» и в строке Подписи оси X ставим маркер. После чего сдвинем это окно так, чтобы можно было увидеть ту колонку таблицы, где ²сидят² наши данные по аргументу x. Выделим весь этот столбец – на графике по оси абсцисс появятся фактические значения аргумента.

11. Совершим затем следующий, третий шаг (клавиша «Далее»). Он позволяет указать конкретные параметры диаграммы. Запустив вкладку Заголовки, присвоим название диаграмме ("Экспериментальная зависимость"), а также отметим оси координат (записываем символы X и Y). По желанию можно "украсить" график – добавить или убрать сетку (вкладка «Линии сетки»), дать необходимые комментарии к графику (вкладка «Легенда»).

12. Последний шаг – укажем, где желательно разместить график. Для этого вновь нажимаем на кнопку «Далее» и отмечаем место расположения его – на имеющемся листе или же отдельном. После завершения этой процедуры последняя приятная операция – прикоснуться к кнопке Готово. Получаем график (Рис.6).

Рис.6 Экспериментальная зависимость

13. Может оказаться, что габариты графика нас решительно не устраивают. Для придания ему более благообразного и удобного вида выделим Область диаграммы (должны появиться по периметру маркеры-засечки) и поменяем размеры (указатель мыши подведём к маркерам – должны возникнуть двойные стрелки, которые и нужно перемещать). Схожим образом можно изменить габариты самого графика (в пределах имеющейся области диаграммы), выделив Область построения диаграммы.

14. Заключительная процедура нашей работы (своеобразный "высший пилотаж" статистической обработки результатов измерения) – это аналитическое описание построенной экспериментальной зависимости. Для этого подведём стрелку мыши к линии графика и щёлкнем правой клавишей. Появится окно Формат рядов данных. Выделим опцию Добавить линию тренда, в результате появится всплывающеё окно Линия тренда.На вкладке Тип выберем похожий на нашу кривую график-шаблон. Для данного случая вполне подходящей оказывается полиноминальную зависимость второй степени (квадратное уравнение). Перейдём затем к вкладке Параметры и укажем засечками команды Показать уравнение на диаграмме и Поместить на диаграмме величину достоверной аппроксимации R². После нажатия клавиши ОК график примет окончательный вид маленького компьютерного шедевра. Отметим, что наша экспериментальная кривая практически полностью совпала с теоретической. Это и неудивительно, поскольку аппроксимирующий коэффициент близок к 1 – идеальное соответствие (Рис.8)!

Фактически данную работу на этом можно считать и законченной. Однако сделаем ещё некоторые оценки. Дело в том, что мы, пользуясь эталонным набором кривых аналитических зависимостей (вкладка Тип из окна Формат рядов данных), удачно выбрали полиноминальный вид функции. Количественно об этом можно судить по величине аппроксимирующего коэффициента R². Можно вполне обоснованно показать, что выбранная зависимость является, похоже, наилучшей. С этой целью для наглядности проверим и другие функции, нанеся на график соответствующую линию тренда, а также показав получаемые уравнения регрессии и величины коэффициента R ²(Рис.7).

Рис.7 Формат линии тренда

Рис.8 Линейный вид

Такую процедуру нетрудно выполнить, после чего для рассмотренного примера полученные показатели R² для разных уравнений регрессии будут иметь следующий вид:

экспоненциальная - R² =0,9765;

полиномиальная - R² =0,9995;

линейная - R² =0,9963;

степенная - R² =0,9887;

логарифмическая - R² =0,906.

На представленных Рис.7-10 нанесены линии аппроксимирующих выражений, даны сами уравнения и показаны рассчитанные значения коэффициента R².

Рис.9 Экспоненциальный вид

Рис.9 Полиномиальный вид

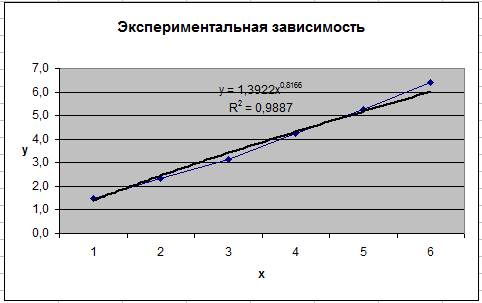
Рис.10 Степенной вид

Рис.11 Логарифмический вид

Как видно, обсуждаемая зависимость y=f(x) лучше всего, как и предполагалось, описывается полиномиальным уравнением. Этот вывод базируется не только на визуальных впечатлениях (вполне адекватное совпадение экспериментальной кривой и линии тренда), но и на строгом количественном расчёте с использованием статистического коэффициента R². Вместе с тем можно утверждать, что ещё более обоснованным представляется описание аппроксимации в виде экспоненциального уравнения, поскольку в этом случае рассчитанное значение коэффициента фактически оказывается равным единице R² =0,9995.